Контрольная работа / Решение 12038 задача 2

Проверить выполнение условий Коши-Римана для функции f(z).

Теория:

Если f(z) = f(x+iy) = u(x, y) + iv(x, y), т.е. u(x, y) = Re f(z) и v(x, y) = Im f(z), то справедливо следующее утверждение:

если функция f(z) дифференцируема в точке, то в этой точке существуют частные производные ее действительной и мнимой частей u(x, y) = Re f(z), v(x, y) = Im f(z) и выполняется условие Коши-Римана:

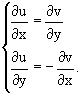
Вариант 7.

Решение:

Для нашей функции:

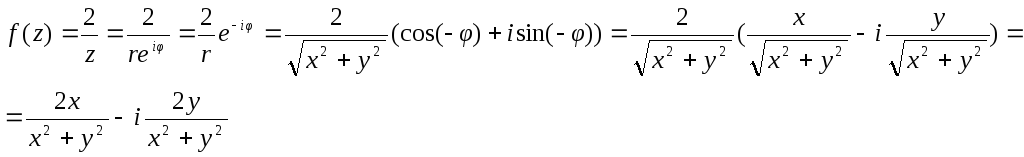
Следовательно:

Получили, что условия Коши-Римана выполняются.

Ответ: условия Коши-Римана выполняются.

Вариант 14.

Решение:

Учтем, что

Для нашей функции:

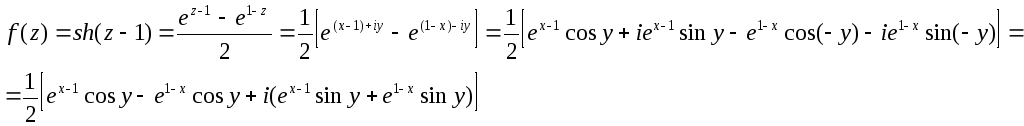Следовательно:

Получили, что условия Коши-Римана выполняются.

Ответ: условия Коши-Римана выполняются.

Вариант 15.

Решение:

Учтем, что

Для нашей функции:

Следовательно:

Получили, что условия Коши-Римана выполняются.

Ответ: условия Коши-Римана выполняются.

Вариант 16.

Решение:

Учитывая, что

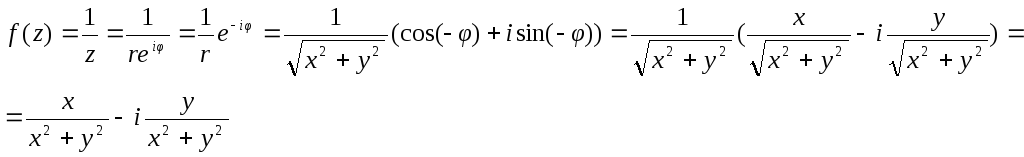
для заданной функции получим:

Следовательно:

Получили, что условия Коши-Римана выполняются в случае, если:

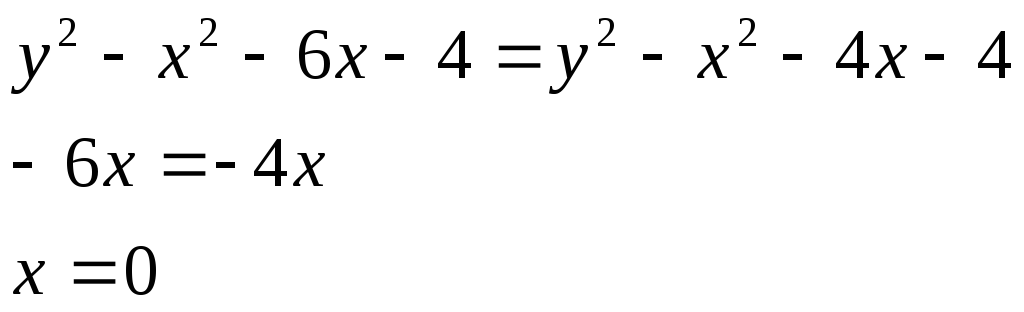
Ответ: условия Коши-Римана выполняются на числовой оси x = 0.

Вариант 18.

Решение:

Для заданной функции:

Следовательно:

Получили, что условия Коши-Римана выполняются.

Ответ: условия Коши-Римана выполняются.