Контрольная работа / Решение 12038 задача 4

Найти вычеты функции f(z) во всех особых точках с помощью пределов.

Теория:

Поскольку числитель и знаменатель дроби - аналитические функции, то особыми точками являются нули знаменателя.

В полюсе a кратности n вычет может быть вычислен по формуле:

Вариант 7.

Решение:

Найдем нули знаменателя, т.е. корни уравнения:

Получили 2-е особые точки кратности n = 2.

Для z = 1:

Для z = 2:

Ответ:

Вариант 14.

Решение:

Найдем нули знаменателя, т.е. корни уравнения:

Для z = 0:

Для z = -4 (кратности 2):

Ответ:

Вариант 15.

Решение:

Найдем нули знаменателя, т.е. корни уравнения:

Для z = -2 (кратности 2):

Для z = 1:

Ответ:

Вариант 16.

Решение:

Найдем нули знаменателя, т.е. корни уравнения:

Для z = 0:

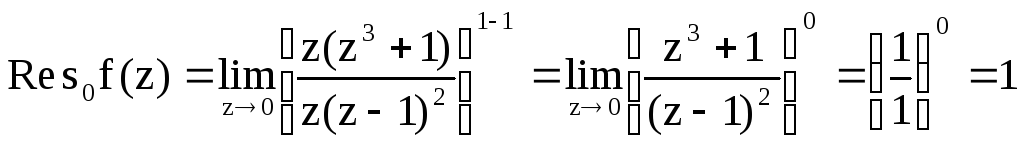
Для z = 1 (кратности 2):

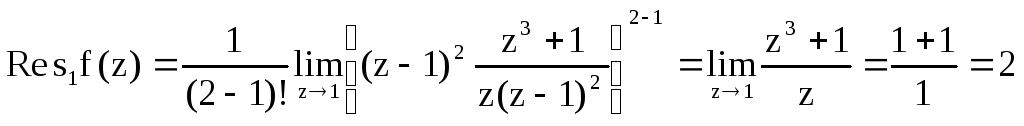
Ответ:

Вариант 18.

Решение:

Найдем нули знаменателя, т.е. корни уравнения:

Для z = 0:

Для z = -1 (кратности 2):

Ответ: