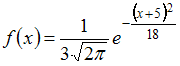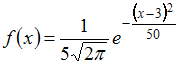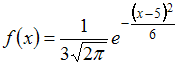Теория вероятностей

  ЗАДАНИЕ N 11 сообщить об ошибке Тема: Теоремы сложения и умножения вероятностей Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый вопрос, равна 0,7, на второй – 0,9, на третий – 0,6. Тогда вероятность того, что студент сдаст экзамен, если для этого необходимо ответить, по крайней мере, на два вопроса, равна …

			0,834
			0,456
			0,378
			0,844

Решение: Введем обозначения событий: A_k (студент знает ответ на k – ый вопрос), A (студент ответит, по крайней мере, на два вопроса).

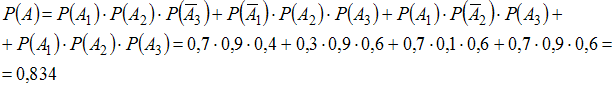
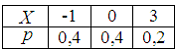
  ЗАДАНИЕ N 12 сообщить об ошибке Тема: Числовые характеристики случайных величин Дискретная случайная величина  X  задана законом распределения вероятностей: Тогда ее математическое ожидание M(X) и дисперсия D(X) равны …

			М (Х) = 0,2; D (X) = 2,16
			М (Х) = 0,2; D (X) = 2,24
			М (Х) = 0,2; D (X) = 2,0
			М (Х) = 1,0; D (X) = 2,16

Решение: Математическое ожидание дискретной случайной величины вычисляется по формуле 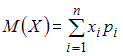. Тогда    Дисперсию дискретной случайной величины X можно вычислить по формуле Тогда

  ЗАДАНИЕ N 13 сообщить об ошибке Тема: Законы распределения вероятностей дискретных случайных величин Дискретная случайная величина X задана законом распределения вероятностей: Тогда вероятность  равна …

			0,8
			0,3
			0,7
			0,4

Решение:

  ЗАДАНИЕ N 14 сообщить об ошибке Тема: Определение вероятности Игральная кость бросается три раза. Тогда вероятность того, что сумма выпавших очков – шестнадцать, равна …

			0

Решение: Для вычисления события A (сумма выпавших очков будет равна 16) воспользуемся формулой  где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны  элементарных исходов испытания, из которых благоприятствующими являются исходы вида          и   то есть m = 6. Следовательно,

  ЗАДАНИЕ N 21 сообщить об ошибке Тема: Числовые характеристики случайных величин Случайная величина X распределена нормально с математическим ожиданием  и дисперсией  Тогда ее плотность распределения вероятностей имеет вид …

Решение: Плотность распределения вероятностей нормально распределенной случайной величины X имеет вид 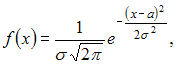 где    Поэтому  Тогда

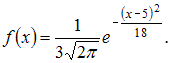
  ЗАДАНИЕ N 23 сообщить об ошибке Тема: Законы распределения вероятностей дискретных случайных величин Для дискретной случайной величины X: функция распределения вероятностей имеет вид: 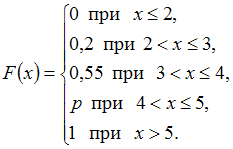Тогда значение параметра p может быть равно …

			0,655
			1
			0,25
			0,45

Решение: По определению  Следовательно,  и  Этим условиям удовлетворяет, например, значение

  ЗАДАНИЕ N 24 сообщить об ошибке Тема: Определение вероятности Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – десять, равна …

			0

Решение: Для вычисления события A (сумма выпавших очков будет равна десяти) воспользуемся формулой , где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны  элементарных исходов испытания, из которых благоприятствующими являются исходы вида ,  и , то есть m = 3. Следовательно,

  ЗАДАНИЕ N 19 сообщить об ошибке Тема: Законы распределения вероятностей дискретных случайных величин Дискретная случайная величина X задана законом распределения вероятностей: И вероятность  Тогда значения  a, b и c могут быть равны …

			a = 0,05, b = 0,30, с = 0,25
			a = 0,05, b = 0,30 с = 0,35
			a = 0,05, b = 0,20 с = 0,35
			a = 0,15, b = 0,30 с = 0,25

Решение: Так как сумма вероятностей возможных значений X равна 1, то  А так как  то  Следовательно, , и, например,  

  ЗАДАНИЕ N 20 сообщить об ошибке Тема: Определение вероятности Внутрь круга радиуса 4 наудачу брошена точка. Тогда вероятность того, что точка окажется вне вписанного в круг квадрата, равна …

Решение: Для вычисления вероятности искомого события воспользуемся формулой  где  – площадь круга, а  – площадь вписанного в круг квадрата. Следовательно,

  ЗАДАНИЕ N 21 сообщить об ошибке Тема: Числовые характеристики случайных величин Математическое ожидание дискретной случайной величины X, заданной законом распределения вероятностей: равно 4,4. Тогда значение вероятности p₂ равно …

			0,7
			0,3
			0,6
			0,4

Решение: Математическое ожидание дискретной случайной величины вычисляется по формуле 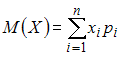. Тогда    А с учетом условия  получаем систему уравнений: 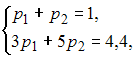  решение которой имеет вид: ,

  ЗАДАНИЕ N 22 сообщить об ошибке Тема: Теоремы сложения и умножения вероятностей Наладчик обслуживает три станка. Вероятность того, что в течение часа потребует его вмешательства первый станок, равна ; второй – ; третий – . Тогда вероятность того, что в течение часа потребуют вмешательства наладчика все три станка, равна …

			0,0015
			0,4
			0,015
			0,9985

Решение: Введем обозначения событий: A_k (вмешательства наладчика потребует k – ый станок), A (вмешательства наладчика потребуют все три станка). Тогда