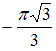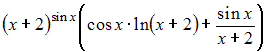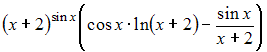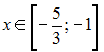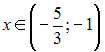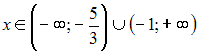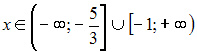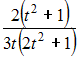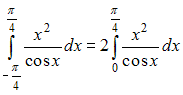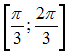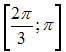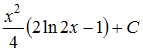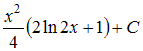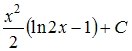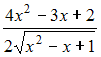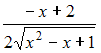Дифференциальное и интегральное исчисление

  ЗАДАНИЕ N 8 сообщить об ошибке Тема: Предел функции Предел 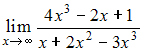 равен …

			4
			1

Решение: 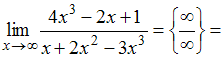Разделим почленно числитель и знаменатель на , где  – степень многочлена в знаменателе. То есть разделим на .

  ЗАДАНИЕ N 19 сообщить об ошибке Тема: Асимптоты графика функции Наклонная  асимптота графика функции 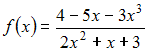 задается уравнением вида …

Решение: Прямая  является наклонной асимптотой графика функции  при    если существуют конечные пределы:     или соответственно    Вычислим эти пределы: 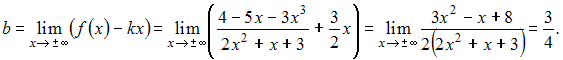Следовательно, прямая  является наклонной асимптотой графика данной функции как при  так и при

  ЗАДАНИЕ N 20 сообщить об ошибке Тема: Основные методы интегрирования Множество первообразных функции  имеет вид …

Решение: Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда 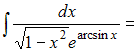Произведем замену    

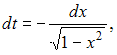
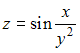  ЗАДАНИЕ N 21 сообщить об ошибке Тема: Дифференциальное исчисление ФНП Значение частной производной  функции  в точке 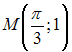 равно …

Решение: При вычислении частной производной  по переменной  y  переменную  x  рассматриваем как постоянную величину. Тогда Следовательно,

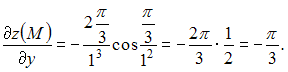
  ЗАДАНИЕ N 22 сообщить об ошибке Тема: Производные первого порядка Производная функции  равна …

Решение: Предварительно прологарифмируем данную функцию:  и продифференцируем обе части полученного равенства 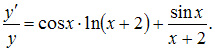Тогда

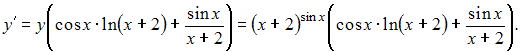
  ЗАДАНИЕ N 23 сообщить об ошибке Тема: Предел функции Предел 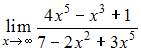 равен …

			1

Решение: 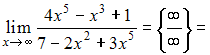Разделим почленно числитель и знаменатель на  где n – степень многочлена в знаменателе, то есть разделим на

  ЗАДАНИЕ N 24 сообщить об ошибке Тема: Область определения функции Область определения функции  имеет вид …

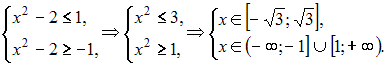Решение: Данная функция определена, если  Тогда Следовательно, область определения данной функции будет иметь вид:

  ЗАДАНИЕ N 25 сообщить об ошибке Тема: Приложения дифференциального исчисления ФОП Материальная точка движется прямолинейно по закону  Тогда скорость точки равна 10 в момент времени …

Решение: Скорость движения  материальной точки можно определить как производную первого порядка пути  по переменной t. Тогда  и  То есть  и с учетом условия  получаем, что

  ЗАДАНИЕ N 26 сообщить об ошибке Тема: Свойства определенного интеграла Среднее значение функции  на отрезке  равно …

Решение: Среднее значение функции  непрерывной на отрезке  вычисляется по формул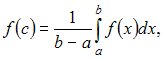е  где  Тогда

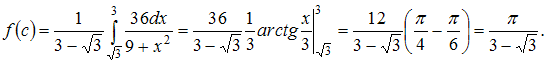
  ЗАДАНИЕ N 25 сообщить об ошибке Тема: Асимптоты графика функции Вертикальная асимптота графика функции 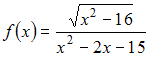 задается уравнением вида …

Решение: Прямая  является вертикальной асимптотой графика функции  если эта функция определена в некоторой окрестности точки  и  или  Вертикальные асимптоты обычно сопутствуют точкам разрыва второго рода. Определим точки разрыва данной функции. Это точки, в которых знаменатель равен нулю, то есть    или    Однако точка  не принадлежит области определения функции  имеющей вид Вычислим односторонние пределы функции  в точке  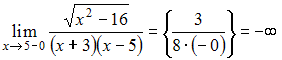и Следовательно, прямая  будет вертикальной асимптотой.

  ЗАДАНИЕ N 27 сообщить об ошибке Тема: Область определения функции Область определения функции  имеет вид …

Решение: Данная функция определена, если  То есть  или

  ЗАДАНИЕ N 28 сообщить об ошибке Тема: Приложения дифференциального исчисления ФОП Промежуток убывания функции 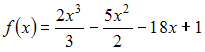 имеет вид …

Решение: Применим достаточное условие убывания функции, которое можно сформулировать следующим образом: если в некотором промежутке  то функция  в этом промежутке убывает. Поэтому вычислим производную первого порядка  и решим неравенство Предварительно найдем корни уравнения  а именно Тогда Следовательно,  при

  ЗАДАНИЕ N 29 сообщить об ошибке Тема: Производные первого порядка Функция  задана в параметрическом виде Тогда производная первого порядка функции  по переменной  x  имеет вид …

Решение:

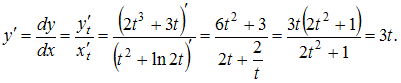
  ЗАДАНИЕ N 30 сообщить об ошибке Тема: Свойства определенного интеграла Для определенного интеграла  справедливо равенство …

Решение: Пусть  Тогда 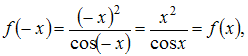то есть функция  является четной. А определенный интеграл от четной функции  по симметричному интервалу  можно представить как

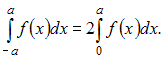
  ЗАДАНИЕ N 31 сообщить об ошибке Тема: Основные методы интегрирования Множество первообразных функции 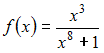 имеет вид …

Решение: Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда 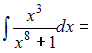Произведем замену    

  ЗАДАНИЕ N 1 сообщить об ошибке Тема: Свойства определенного интеграла Значение определенного интеграла  принадлежит промежутку …

Решение: Если функция  интегрируема на    и  то 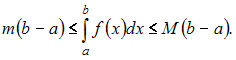Согласно свойств функции  наименьшее значение функции  на отрезке  достигается при  и равно  а наибольшее – при  и равно 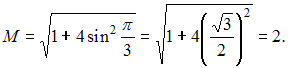Следовательно, 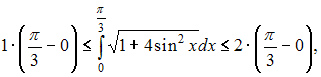 или

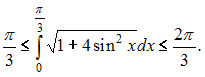
  ЗАДАНИЕ N 3 сообщить об ошибке Тема: Основные методы интегрирования Множество первообразных функции  имеет вид …

Решение: Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции методом интегрирования по частям по формуле  Тогда

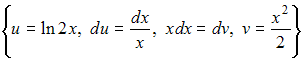
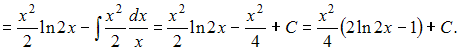
  ЗАДАНИЕ N 5 сообщить об ошибке Тема: Производные первого порядка Производная функции  равна …

Решение:

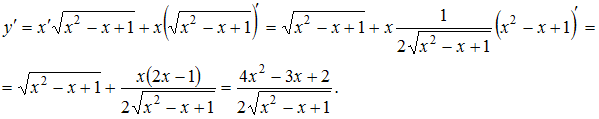
  ЗАДАНИЕ N 7 сообщить об ошибке Тема: Приложения дифференциального исчисления ФОП Уравнение касательной к графику функции  в его точке с абсциссой  имеет вид …

Решение: Уравнение касательной к графику функции  в его точке с абсциссой  имеет вид  Вычислим последовательно    и  Тогда уравнение касательной примет вид  или