
- •Бочанова ю.В. Ю.В. Бочанов., и.И. Марончук., а.Н. Петраш
- •Предисловие.
- •1. Энергия. Работа. Мощность. Закон сохранения энергии. Примеры решения задач.
- •Работа, совершённая двигателем автомобиля, равна
- •По закону трения
- •Подставим числовые значения,
- •Задачи по вариантам.
- •2. Закон сохранения импульса. Теорема о движении центра масс. Движение тел с переменной массой. Примеры решения задач
- •Варианты.
- •Варианты.
- •4. Закон сохранения момента импульса. Гироскопы. Гироскопические силы. Примеры решения задач.
- •Решение Систему тел можно считать изолированной, поэтому выполняется закон сохранения момента импульса
- •Варианты.
- •5. Движение материальной точки и системы точек в неинерциальных системах отсчёта. Силы инерции. Примеры решения задач.
- •Варианты.
- •6. Поле тяготения. Законы Кеплера. Космические скорости. Примеры решения задач.
- •Варианты.
- •7. Напряжения и деформации в твёрдом теле. Энергия упругих деформаций. Примеры решения задач.
- •Варианты.
- •8. Кинематика теории относительности. Преобразования Лоренца. Примеры решения задач.
- •Продольный размер тела
- •Относительное изменение продольного размера
- •Варианты.
- •8. При какой скорости масса движущейся частицы в три раза больше массы покоя этой частицы?
- •Основные физические постоянные и некоторые астрономические величины.
- •Масса покоя элементарных частиц
- •Плотность вещества
- •Упругие свойства некоторых твёрдых тел.
- •Международная система измерения (система си) Основные единицы измерения
- •Дополнительные единицы измерения
- •Некоторые производные единицы измерения
- •Перевод некоторых наиболее часто встречающихся в задачах внесистемных единиц измерения в систему си
- •Некоторые приставки для преобразования внесистемных единиц в систему си
- •Греческий алфавит
- •Латинский алфавит
- •Моменты инерции однородных тел
- •Основные сведения из математики
- •Формулы приведения
- •Тригонометрические функции половинного аргумента
- •Тригонометрические функции двойного аргумента
- •Формулы сложения
- •Литература
- •3. Динамика вращательного движения твёрдого тела. Динамика плоского движения твёрдого тела 11
8. Кинематика теории относительности. Преобразования Лоренца. Примеры решения задач.
Задача 1. Кинетическая энергия электрона равна 1 МэВ. Определить скорость электрона.
 Решение.
Решение.
Частица называется релятивистской, если скорость частицы сравнима со скоростью света, и классической, если << c. Чтобы определить, какой является частица, достаточно сравнить её кинетическую энергию с энергией покоя.
Энергия
покоя электрона
![]() 9,1·10-31(3·108)2
= 8,2·10-14
Дж = 0,511 МэВ – частица релятивистская,
так как
9,1·10-31(3·108)2
= 8,2·10-14
Дж = 0,511 МэВ – частица релятивистская,
так как
![]()
Релятивистская формула кинетической энергии
 (1)
(1)
откуда находим .
Для
простоты преобразований найдём
![]() то есть скорость частицы, выраженную в
долях скорости света.
то есть скорость частицы, выраженную в
долях скорости света.
Величину
![]() подставим в формулу (1).
подставим в формулу (1).
Выполнив преобразования, получим
![]()
Числовой расчёт удобнее вести, выразив энергию в мегаэлектронвольтах (МэВ):
![]()
Так
как
![]() ,
то
= 0,941· 3·108
= 2,82·108
,
то
= 0,941· 3·108
= 2,82·108
![]() .
.
Ответ: = 2,82·108 .
Задача 2. На сколько процентов изменится продольный размер протона и электрона после прохождения ими разности потенциалов U = 106 В?

Решение.
Заряд протона и электрона имеет одинаковые числовые значения, поэтому они после прохождения разности потенциалов U приобретает одинаковую кинетическую энергию, равную работе электрического поля:
Wе = qU = 1,6·![]() ·
·![]() = 1,6·
= 1,6·![]() Дж = 1 МэВ.
Дж = 1 МэВ.
Продольный размер тела
![]() ,
,
где
![]() – длина в системе, неподвижной относительно
тела; l
– длина
тела, движущегося со скоростью
.
– длина в системе, неподвижной относительно
тела; l
– длина
тела, движущегося со скоростью
.
Относительное изменение продольного размера
Из
релятивистской формулы кинетической
энергии найдём значение
![]() :
:
qU,
откуда

Тогда

Для электрона c2 = 0,511 МэВ; для протона c2 = 939 МэВ.
Подставив числовые данные, получим для электрона
![]()
Для протона
![]()
Ответ:
![]() для электрона и
для электрона и
![]() для протона.
для протона.
Задача 3. Два ускорителя выбрасывают частицы навстречу друг другу со скоростями 0,9с. Определить относительную скорость сближения частиц.
Р ешение.
ешение.
Для решения воспользуемся законом сложения скоростей в релятивисткой механике:

Из
условия
![]() .
Тогда:
.
Тогда: .
.
Ответ:
![]() .
.
Задача 4. Во сколько раз масса протона больше массы электрона, если обе частицы имеют одинаковую кинетическую энергию 1000 МэВ.
Р ешение.
ешение.
Из
формулы определения массы движущейся
частицы в релятивисткой механике выразим
отношение масс:
![]() .
Подставив полученное выражении в формулу
кинетической энергии, получим связь
массы движущейся частицы с энергией:
.
Подставив полученное выражении в формулу
кинетической энергии, получим связь
массы движущейся частицы с энергией:
![]() .
Энергии покоя электрона и протона
величины постоянные и равны:
.
Энергии покоя электрона и протона
величины постоянные и равны:
![]() МэВ
и
МэВ
и
![]() МэВ.
МэВ.
Тогда
массы электрона и протона соответственно
находим как:
![]() кг
и
кг
и
![]() кг.
А их отношение равно:
кг.
А их отношение равно:
![]()
Ответ:
![]() .
.
Задача 5. Мю – мезон, рождающийся в верхних слоях атмосферы, пролетает до распада 6000м. Определить с какой скоростью летит мю – мезон, если его собственное время жизни 2,2 . 10 –6 с.
Р ешение.
ешение.
Скорость
определим из уравнения пути при
равномерном движении:
![]() ,
где время определим по формуле длительности
событий в инерциальных системах отсчёта:
,
где время определим по формуле длительности
событий в инерциальных системах отсчёта:
 .
Тогда можем записать:
.
Тогда можем записать:

Откуда искомая скорость
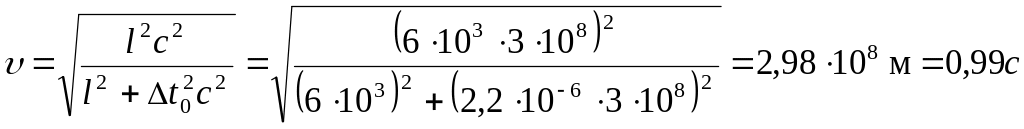
Ответ:
![]() .
.
Задача 6. Частица с массой покоя начала двигаться под действием постоянной силы F. Найти зависимость скорости частицы от времени.
Р ешение.
ешение.
Запишем основное уравнение динамики движения в релятивисткой механике в виде:

Проинтегрировав
это выражение с учётом того, что в
начальный момент
![]() ,
получим
,
получим
 .
Отсюда
.
Отсюда
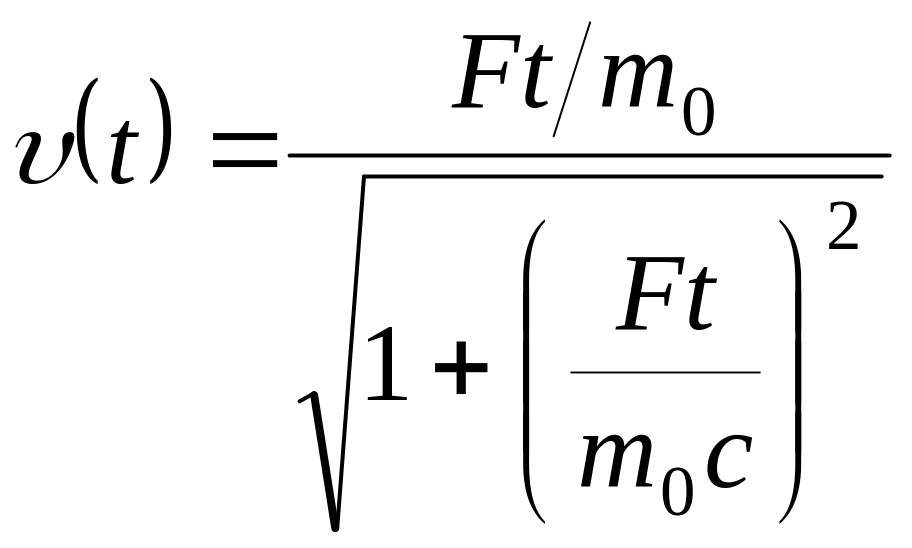 .
.
С равним
полученное выражение с ньютоновским.
Согласно второго закона Ньютона,
равним
полученное выражение с ньютоновским.
Согласно второго закона Ньютона,
![]() и скорость
и скорость
![]() ,
поэтому предыдущее выражение для
скорости
можно представить так:
,
поэтому предыдущее выражение для
скорости
можно представить так:

Отсюда
видно, что
![]() ,
т.е. действительная скорость
частицы растёт со временем медленнее,
чем
,
т.е. действительная скорость
частицы растёт со временем медленнее,
чем
![]() причём при
причём при
![]() скорость
скорость
![]() (см.рис. 8.1).
(см.рис. 8.1).
Интересно,
что импульс частицы при этом будет расти
линейно со временем: из уравнения
![]() .
В этом характерная особенность
релятивисткого движения: в то время как
скорость частицы стремится к определённому
пределу (т.е. практически устанавливается),
импульс частицы продолжает расти.
.
В этом характерная особенность
релятивисткого движения: в то время как
скорость частицы стремится к определённому
пределу (т.е. практически устанавливается),
импульс частицы продолжает расти.
