Варианты.

1. Шар на нити подвешен к потолку трамвайного вагона. Вагон тормозится и его скорость за время с равномерно уменьшается от км/ч до км/ч. На какой угол при этом отклонится нить с шаром.

2. В вагоне, движущемся горизонтально с ускорением м/с ², висит на шнуре груз массой 200 г. Найти силу натяжения шнура и угол отклонения шнура от вертикали.

3. Система грузов массами кг и кг находится в лифте, движущемся вверх с ускорением м/с². Определите силу натяжения нити, если коэффициент трения между грузом массы и опорой .

4 . На клине с углом при основании лежит брусок. Коэффициент трения между бруском и клином . С каким ускорением должен двигаться клин, чтобы брусок не соскальзывал? Задачу решить в системе отсчёта, связанной с клином.

5. Найти период обращения конического математического маятника, нить которого длиной составляет угол с вертикалью (см.рис. 5.5). Решить задачу, воспользовавшись вращающейся системой отсчёта.

6. Диск совершает 70 об/мин. Где можно положить на диск тело, чтобы оно не соскользнуло? Коэффициент трения покоя тела о диск . Задачу решить во вращающейся системе отсчёта, связанной с диском.

7. В аттракционе «мотоциклетные гонки на вертикальной стене» трек представляет собой вертикальную цилиндрическую поверхность диаметром 18 м. С какой скоростью должен двигаться мотоциклист, чтобы не соскальзывать с трека? Коэффициент трения . Решить задачу, воспользовавшись вращающейся системой отсчёта.

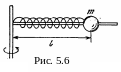
8. Недеформированная пружина с жёсткостью k имеет длину . При вращении системы (см.рис. 5.6) с угловой скоростью груз массой m растягивает пружину. Найти длину l пружины при вращении. Решить задачу, воспользовавшись вращающейся системой отсчёта.

9. По гладким горизонтальным рельсам движется плат­форма массой M со скоростью . На передний край платформы кладут аккуратно (т. е. без толчка) груз массой m. Коэффициент трения между этим грузом и платформой равен . При какой минимальной длине l платформы груз не упадет с нее?

10. Тонкий однородный стержень длиной l, могущий свободно вращаться вокруг горизонтальной оси, про­ходящей через один из его концов, находится в вагоне. Вагон начинает двигаться горизонтально с ускорением , направленным нормально к оси вращения стержня. На какой максимальный угол от вертикали отклонится стержень в начале?

11. К потолку вагона, движущегося в горизонтальном направлении с ускорением м/с², подвешен на нити шарик массой г. Определите для установившегося движения: 1) силу натяжения нити T; 2) угол отклонения нити от вертикали.

12. Вагон под действием силы тяжести катится вдоль дороги, составляющей угол с горизонтом. Сила трения составляет от веса вагона. К потолку вагона на нити подвешен шарик массой г. Определите: 1) силу F, действующую на нить; 2) угол отклонения нити от вертикали.

13. На наклонной плоскости с углом наклона лежит тело. Коэффициент трения между наклонной плоскостью и телом . Определите наименьшее горизонтально направленное ускорение a, с которым должна двигаться наклонная плоскость, чтобы тело, лежащее на ней, поднималось по наклонной плоскости.

14. Самолёт, летящий со скоростью км/ч, описывает вертикальную петлю Нестерова радиусом м. Определите силу, прижимающую лётчика ( кг) к сиденью: 1) в нижней точке этой петли; 2) в верхней точке этой петли.

15. Определите, во сколько раз ускорение , обусловленное центробежной силой на экваторе Земли, меньше ускорения , вызываемого силой тяготения на поверхности Земли.

16. Тело массой кг, падая свободно в течение с, попадает на Землю в точку с географической широтой . Учитывая вращение Земли, определите и нарисуйте все силы, действующие на тело в момент его падения на Землю.

17. Тело массой кг, падая свободно в течение с, попадает на Землю в точку с географической широтой . Учитывая вращение Земли, определите отклонение тела при его падении от вертикали.

18. На гладком клине массой кг расположена материальная точка массой кг. Клин может двигаться по гладкой горизонтальной поверхности. Угол у основания клина . Определить ускорение тела и клина.

19. Горизонтальный диск вращают с постоянной угловой скоростью рад/с вокруг вертикальной оси, проходящей через его центр. По одному из диаметров диска движется небольшое тело массы кг с постоянной скоростью см/с. Найти силу, с которой диск действует на это тело в момент, когда оно находится на расстоянии см от оси вращения.

20. С вершины гладкой сферы радиуса м начинает соскальзывать небольшое тело массой кг. Сфера вращается с постоянной угловой скоростью рад/с вокруг вертикальной оси, проходящей через её центр. Найти в системе отсчёта, связанной со сферой, центробежную силу инерции и силу Кориолиса в момент отрыва тела от поверхности сферы.