11. Анализ производительности проекта параллельной системы

Анализ производительности проекта особенно важен для систем реального вре­мени. Если такая система не справляется со своими задачами в течение отведен­ного интервала, последствия могут быть катастрофическими.

Количественный анализ проекта системы реального времени позволяет на ранних этапах выявить потенциальные проблемы с производительностью. Ана­лизу подвергается проект ПО, концептуально исполняемый на данной аппарат­ной конфигурации с рассчитанной внешней рабочей нагрузкой. Обнаружив веро­ятные проблемы, легко рассмотреть альтернативные подходы к проектированию или иную конфигурацию аппаратуры.

Ниже речь пойдет о способе анализа производительности проекта ПО, осно­ванном на теории планирования в реальном времени. Этот метод прекрасно рабо­тает для систем реального времени, которые должны выдерживать жесткие вре­менные ограничения [24]. Он позволяет определить, будут ли выполнены наложенные ограничения.

Мы опишем два подхода к анализу производительности. В первом использу­ется теория планирования в реальном времени, а во втором – анализ последова­тельности событий. Затем мы объединим оба подхода. Каждый из них применим к проектам, состоящим из набора параллельных задач. Следовательно, анализ производительности можно начинать сразу после проектирования архитектуры задач.

11.1. Теория планирования в реальном времени

В теории планирования в реальном времени рассматриваются вопросы приори­тетного планирования параллельных задач с жесткими временными ограничени­ями. В частности, она позволяет предсказать, будет ли группа задач, для каждой из которых потребление ресурсов ЦП известно, удовлетворять этим ограничени­ям. В теории предполагается использование алгоритма приоритетного планиро­вания с вытеснением.

По мере своего развития теория планирования в реальном времени применя­лась к все более сложным задачам, в числе которых планирование независимых периодических задач, планирование в ситуации, когда есть и периодические, и апериодические (асинхронные) задачи, а также планирование задач, требующих синхронизации.

11.1.1. Планирование периодических задач. Изначально алгоритмы планирования в реальном времени разрабатывались для независимых периодических задач, то есть таких периодических задач, кото­рые не взаимодействуют друг с другом и, следовательно, не нуждаются в синхро­низации. С тех пор было проведено множество теоретических исследо­ваний, результаты которых теперь можно применять к практическим задачам, что и будет продемонстрировано на примерах. Но начнем мы с базового метода моно­тонного анализа частот для независимых периодических задач, чтобы понять, как обобщить его на более сложные ситуации.

Периодическая задача характеризуется периодом Т (частота запуска) и вре­менем выполнения С (время ЦП, необходимое для завершения одного запуска). Коэффициент использования ЦП для нее равен U = С/Т. Задача называется пла­нируемой (schedulable), если она удовлетворяет всем временным ограничениям, то есть ее исполнение завершается до истечения периода. Группа задач именуется планируемой, когда планируемой является каждая входящая в нее задача.

Если дано множество независимых периодических задач, то алгоритм моно­тонных частот назначает каждой задаче фиксированный приоритет, вычисляе­мый на основе ее периода: чем короче период, тем выше приоритет. Рассмотрим задачи t_a, t_b и t_c с периодами 10, 20 и 30 соответственно. Наивысший приоритет будет назначен задаче t_a с самым коротким периодом, средний приоритет - задаче t_b а самый низкий – задаче t_c, период которой максимален.

11.1.2. Теорема о верхней границе коэффициента использования ЦП. Пользуясь теорией планирования, можно показать, что группа независимых пе­риодических задач всегда удовлетворяет временным ограничениям при условии, что сумма отношений С/Т по всем задачам меньше некоторого граничного значения.

Теорема о верхней границе коэффициента использования ЦП (теорема 1) гласит:

Множество из п независимых периодических задач, планируемых согласно алго­ритму монотонных частот, всегда удовлетворяет временным ограничениям, если

где С_i и Т_i – время выполнения и период задачи t_i соответственно.

Верхняя граница U(n) стремится к 69% (ln 2), когда число задач стремится к бесконечности. Значения верхней границы для числа задач от 1 до 9 приведены в табл.11.1. Это оценка для худшего случая, но, как показано в работе [22], для случайно выбранной группы задач вероятная верхняя граница равна 88%. Если периоды задач гармоничны (являются кратными друг другу), то верхняя граница оказывается еще выше.

Таблица 11.1

Теорема о верхней границе коэффициента использования

Число задач n	Верхняя граница коэффициента использования U(n)
1	1,000
2	0,828
3	0,779
4	0,756
5	0,743
6	0,734
7	0,728
8	0,724
9	0,720
Бесконечность	0,690

Достоинство алгоритма монотонных частот заключается в том, что он сохра­няет устойчивость в условиях краткосрочной перегрузки. Другими словами, под­множество всего множества задач, состоящее из задач с наивысшими приоритета­ми (то есть наименьшими периодами), все еще будет удовлетворять временным ограничениям, если система в течение короткого промежутка времени подверга­ется сверхрасчетной нагрузке. Задачи с низкими приоритетами по мере повыше­ния загрузки процессора могут эпизодически выполняться дольше положенного времени.

Применим теорему о верхней границе коэффициента использования к трем задачам со следующими характеристиками (время всюду выражено в миллисе­кундах):

Задача t₁: С₁ ⁼ 20; Т₁ ⁼ 100; U₁= 0,2.

Задача t₂: C₂ = 30; Т₂ = 150; U₂= 0,2.

Задача t₃: С₃ = 60; Т₃ = 200; U₃= 0,3.

Предполагается, что накладные расходы на контекстное переключение, про­исходящее один раз в начале и один раз в конце выполнения задачи, содержатся в оценке времени ЦП.

Полный коэффициент использования ЦП для всех трех задач равен 0,7, что ниже, чем величина 0,779, которую дает теорема о верхней границе. Таким обра­зом, эти задачи будут удовлетворять временным ограничениям.

Но попробуем изменить характеристики третьей задачи:

Задача t₃: C₃ = 90; Т₃ = 200; U₃= 0,45.

Теперь полный коэффициент использования ЦП равен 0,85, то есть выше, чем 0,779. Следовательно, теорема о верхней границе не дает гарантии, что задачи смо­гут удовлетворить временным ограничениям. Далее нужно проверить, так ли это для первых двух задач.

Принимая во внимание устойчивость алгоритма монотонных частот, для по­добной проверки допустимо применить теорему о верхней границе коэффициен­та использования ЦП. Для первых двух задач полный коэффициент равен 0,4, то есть намного ниже значения, полученного из теоремы (0,828). Значит, эти задачи всегда удовлетворяют временным ограничениям. Учитывая, что теорема о верх­ней границе дает пессимистическую оценку, мы можем проверить, является ли задача t₃ планируемой, посредством более точной теоремы о времени завершения.

11.1.3. Теорема о времени завершения. Если для некоторого множества задач полный коэффициент использования больше, чем требует теорема о верхней границе, то можно прибегнуть к помощи теоремы о времени завершения [22], которая дает более достоверный критерий. Она позволяет точно определить, является ли данное мно­жество независимых периодических задач планируемым. В этой теореме предпо­лагается худший случай, когда все периодические задачи готовы к исполнению одновременно. Если в указанных условиях выполнение задачи завершается до истечения ее первого периода, то она всегда будет удовлетворять временным огра­ничениям [22]. Таким образом, теорема о времени завершения проверяет, способна ли каждая задача завершить­ся до истечения своего первого периода.

Теорема о времени завершения (теорема 2) гласит:

Если имеется такое множество независимых периодических задач, в котором каждая задача успевает завершиться вовремя в случае, когда все задачи запуска­ются одновременно, то все задачи смогут завершиться вовремя при любой комби­нации моментов запуска.

Чтобы убедиться в выполнении условий теоремы, необходимо проверить мо­мент завершения первого периода для данной задачи t_i, а также моменты завер­шения периодов всех задач с более высоким приоритетом. Согласно алгоритму монотонных частот, периоды подобных задач будут меньше, чем для задачи t_i. Эти периоды называются точками планирования. Задача t. один раз займет ЦП на вре­мя С_i в течение своего периода Т_i. Но более приоритетные задачи будут выпол­няться чаще и могут по крайней мере один раз вытеснить t_i. Поэтому нужно учесть также время ЦП, затраченное на более приоритетные задачи.

Теорема о времени завершения графически представляется с помощью вре­менной диаграммы, на которой показана упорядоченная по времени последова­тельность выполнения группы задач. Рассмотрим три приведенные выше задачи со следующими характеристиками:

Задача t₁: С₁ = 20; Т ₁= 100; U₁= 0,2.

Задача t₂: C₂ = 30; T₂ = 150; U₂= 0,2.

Задача t₃: C₃ = 90; T₃ = 200; U₃= 0,45.

Их выполнение показано на временной диаграмме на рис.11.1. В методе COMET временная диаграмма – это диаграмма последовательности с временны­ми метками. Заштрихованные участки обозначают интервалы времени, в течение которых реализуется данная задача. Поскольку в приведенном примере есть все­го один процессор, то в каждый момент времени выполняется только одна задача.

В худшем случае, когда все три задачи готовы к работе одновременно, первой запускается t₁, так как у нее самый короткий период и, значит, самый высокий приоритет. Она завершается по прошествии 20 мс, после чего в течение 30 мс ис­полняется задача t₂ а затем t₃ В конце первой точки планирования Т₁ = 100, что соответствует сроку завершения t₁; t₁ уже завершена и, следовательно, удовлетво­ряет временным ограничениям. Задача t₂ также завершила работу задолго до сро­ка, а задача t₃ потратила 50 мс из необходимых 90.

В начале второго периода t₁ задача t₃ вытесняется задачей t₃. Проработав 20 мс, t₂ завершается и уступает процессор задаче t₃. Задача t₃ выполняется до конца пе­риода Т₂ (150 мс), который соответствует второй точке планирования, определя­емой сроком завершения t₂. Поскольку t₂ завершилась до момента Т₁ (меньшего, чем Т₂), то она уложилась в отведенный для нее срок. В этот момент t₃ использовала 80 мс из необходимых 90.

В начале второго периода задачи t₂ она вытесняет задачу t₃ Проработав 30 мс, t₂ завершается и возвращает процессор задаче t₃ Задача t₃ исполняется еще 10 мс, И в этот момент заканчиваются ее 90 мс, то есть она успела завершиться до исте­чения своего срока. На рис.11.1 изображена третья точка планирования, которая расположена в конце второго периода t₁ (2T₁= 200) и одновременно в конце пер­вого периода t₃ (T₃ = 200). Из рисунка видно, что каждая задача завершает испол­нение до конца своего первого периода, так что все вместе они удовлетворяют вре­менным ограничениям.

На рис.11.1 показано, что ЦП простаивает 10 мс перед началом третьего пе­риода t₁ (этот момент совпадает с началом второго периода t₃). Отметим, что на протяжении интервала длительностью 200 мс процессор работал 190 мс, то есть задействовался на 95%, хотя полный коэффициент использования равен 0,85. По истечении времени, равного наименьшему общему кратному трех периодов (для данного примера 600 мс) средний коэффициент использования оказывается рав­ным 0,85.

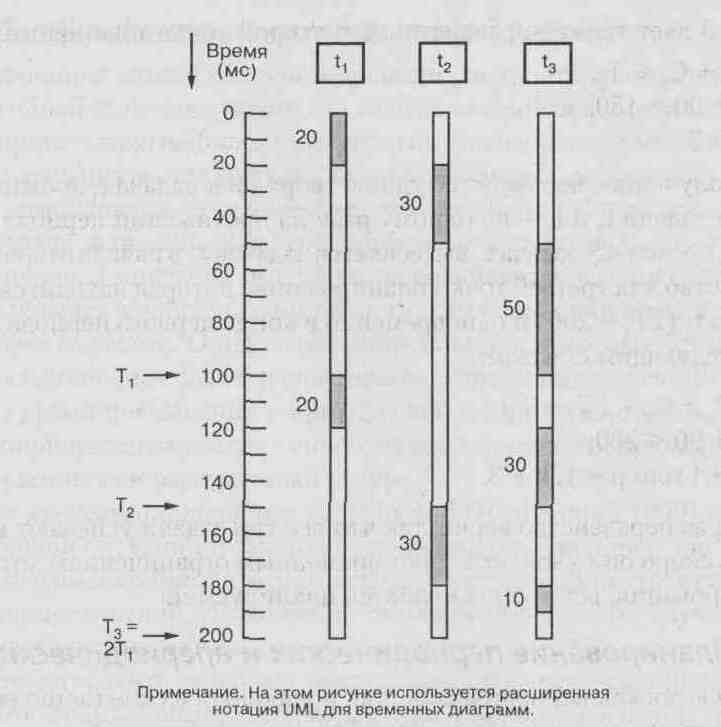
Рис.17.1. Временная диаграмма (диаграмма последовательности с временными метками)

11.1.4. Строгая формулировки теоремы о времени завершения.

Теорему о времени завершения можно строго сформулировать следующим образом [24] (теорема 3):

Множество независимых периодических задач, планируемых согласно алгорит­му монотонных частот, будет удовлетворять временным ограничениям при любой комбинации моментов запуска тогда и только тогда, когда

,

где С_i и Т_i – время выполнения и период задачи t_j соответственно, а

R_i = {(k,p): l≤k≤i, p=l,...,[T_i/T_k]}.

В этой формуле t_i – это проверяемая задача, a t_k – любая из более приоритетных задач, влияющих на время выполнения t_i. Для данной пары задач t_i и t_k каждое зна­чение р представляет некоторую точку планирования задачи t_k. В каждой точке планирования необходимо рассмотреть один раз время ЦП С_i, потраченное на зада­чу t_i, а также время, израсходованное на более приоритетные задачи. Это позволит определить, успеет ли t_i завершить выполнение к данной точке планирования.

Рассмотрим применение теоремы 3 к трем задачам, показанным на рис.11.1. Временная диаграмма – это графическое представление вычислений, выполняе­мых в теореме 3. Снова обратимся к худшему случаю, когда все три задачи одно­временно готовы к выполнению. Из теоремы 3 вытекает неравенство для первой точки планирования Т₁ = 100:

С₁ + C₂+ С₃ < Т₁;

20 + 30 + 90 > 100;

p=l, k=l.

Чтобы это неравенство удовлетворялось, все три задачи должны завершиться на протяжении первого периода Т₁ задачи t₁. Это не так: прежде чем задача t₃ успе­вает завершиться, ее вытесняет задача t₁ в начале своего второго периода.

Теорема 3 дает также неравенство для второй точки планирования Т₂ = 150:

2С₁ + С₂ + С₃ ≤ Т₂;

40 + 30 + 90 > 150;

p=l, k=2.

Чтобы полученное неравенство удовлетворялось, задача t₁ должна завершить­ся дважды, а задачи t₂ и t₃ – по одному разу на протяжении периода Т₂ задачи t₂. И это не так, поскольку задача t₃ вытесняется задачей t₂ в начале второго периода t₂.

Неравенство для третьей точки планирования, которая находится в конце вто­рого периода t₁ (2Т₁ = 200) и одновременно в конце первого периода t₃ (T₃ = 200), выглядит следующим образом:

2С₁ + 2С₂ + C₃ ≤ 2Т1 = Т₃;

40 + 60 + 90 < 200;

р = 2, k = 1 или р = 1, k = 3.

На этот раз неравенство верно, так что все три задачи успевают выполниться в срок. Коль скоро они удовлетворяют временным ограничениям хотя бы в одной точке планирования, вся группа является планируемой.

11.1.5. Планирование периодических и апериодических задач. Если имеются как периодические, так и апериодические (асинхронные) зада­чи, то алгоритм монотонных частот необходимо обобщить. Предполагается, что апериодическая задача активизируется в случайный момент времени и выполня­ется один раз в течение некоторого промежутка времени Т_a, который обозначает минимальное время между последовательными возникновениями события, акти­визирующего эту задачу. Время ЦП С_a, необходимое апериодической задаче для обработки события, резервируется на каждом периоде Т_a как своего рода квота. Когда поступает событие, апериодическая задача активизируется, запрашивает квоту и потребляет до С_a единиц процессорного времени. Если в течение периода Т_a задача так и не была активизирована, квота на этот период аннулируется. В дан­ных предположениях коэффициент использования ЦП апериодической задачей равен С_a/Т_a. Однако здесь приведена оценка для худшего случая, так как, вообще говоря, квоты требуются не всегда.

Если в приложении имеется много апериодических задач, разрешается вос­пользоваться алгоритмом спорадического сервера [25]. С точки зрения анализа планируемости апериодическая задача (называемая спо­радическим сервером) эквивалентна периодической задаче с периодом, равным минимальному времени между возникновениями событий, которые активизиру­ют апериодическую задачу. Поэтому Т_a удобно считать периодом эквивалентной периодической задачи. Каждой апериодической задаче выделяется бюджет, рав­ный С_a единиц времени процессора, который может быть использован в любой момент на протяжении периода Т_a. Таким образом, апериодическим задачам до­пустимо назначить различные уровни приоритета в соответствии с эквивалент­ными периодами и рассматривать их как периодические.

11.1.6. Планирование с синхронизацией задач. Теория планирования в реальном времени распространяется и на синхрони­зацию задач. Проблема здесь в том, что задача, входящая в критическую область, может блокировать другие более приоритетные задачи, которые хотят войти в ту же область. Ситуация, когда низкоприоритетная задача не дает выполняться высокоприоритетной, называется инверсией приоритетов. Обычно это связано с тем, что первая задача захватывает ресурс, который нужен второй.

Неограниченная инверсия приоритетов возникает, когда низкоприоритетная задача, находящаяся в критической области, сама заблокирована другими более приоритетными задачами. Одно из решений данной проблемы состоит в том, что­бы запретить вытеснение задач, находящихся в критической секции. Но это при­емлемо, если время пребывания в критической секции очень мало. В противном случае низкоприоритетная задача способна заблокировать высокоприоритетные задачи, которым нужен разделяемый ресурс.

Протокол предельного приоритета [24] позволяет из­бежать тупиковой ситуации и гарантирует ограниченную инверсию приоритетов за счет того, что высокоприоритетная задача может блокироваться самое большее одной низкоприоритетной. Ниже мы рассмотрим простейший случай, когда есть всего одна критическая секция.

Чтобы предотвратить задержку высокоприоритетных задач низкоприоритет­ными на долгое время, применяется коррекция приоритетов. Когда низкоприори­тетная задача t₁ оказывается в критической области, она в состоянии блокировать высокоприоритетные задачи, которым нужен тот же ресурс. Если это происходит, то приоритет t₁ повышается до максимального из приоритетов блокируемых за­дач. Цель состоит в том, чтобы ускорить выполнение низкоприоритетной задачи и сократить время ожидания для высокоприоритетных.

Предельный приоритет Р двоичного семафора S – максимум из приоритетов всех задач, которые могут занять данный семафор. Таким образом, низкоприори­тетная задача, захватившая S, способна повысить свой приоритет до Р в зависи­мости от того, какие задачи она блокирует.

Еще одна возможная проблема – это тупиковая ситуация (deadlock), которая возникает, когда двум задачам нужно захватить по два ресурса. Если каждая задача захватит по одному ресурсу, то ни одна не сможет завершиться, поскольку будет ждать, пока другая освободит ресурс. Протокол предельного приоритета справля­ется и с такой трудностью [24].

Теоремы о планировании методом монотонных частот необходимо обобщить на задачу об инверсии приоритетов. В следующем разделе мы покажем, как это сделать.