Коефіцієнти еластичності результативного показника по факторах визначаються за формулою (24)

(24)

Коефіцієнт еластичності по є безрозмірним показником, він

визначає вплив цього фактора на показник. Якщо зміниться на 1%, то зміниться на %. Оскільки для лінійної регресії коефіцієнт еластичності залежить від , то найчастіше обчислюють коефіцієнт еластичності для середнього .

Згідно з моделлю (20): коефіцієнти еластичності, знайдені за формулою (24) для факторних змінних, дорівнюють:

;

,

де , , розраховані раніше (формули (17)-(19)).

Отже, якщо загальні витрати зміняться на 1%, то витрати на харчування зміняться на % при умові, що решта факторів не змінюється. Якщо кількість членів сім’ї зміниться на 1%, то витрати на харчування зміняться на % при умові, що решта факторів не змінюється.

Нехай ми бажаємо розповсюдити побудовану модель на інші значення факторних змінних і поставити проблему прогнозування середнього значення , яке відповідає деяким даним значенням змінних Причому ці нові значення можуть лежати як між вибірковими спостереженнями, так і поза відповідних інтервалів. Точечний прогноз представляє з себе обчислене по рівнянню (14) значення (25)

. (25)

Обчислимо попередній прогноз для сім’ї з загальними витратами умовних грошових одиниць і складом сім’ї чоловік. Тоді за формулою (25) слід очікувати, що витрати на харчування, складуть умовних грошових одиниць.

5 Рангова кореляція

Аналіз економічних процесів стикається з необхідністю вивчення взаємозв’язків, які не мають кількісного вимірювача. Це соціологічні, узагальнені соціально-економічні характеристики, що впливають на хід економічного процесу. Наприклад, рішення питання задовільнення попиту на товари залежить від асортименту товарів, рівня взаємовідносин виробників із споживачами, умов транспортування і зберігання продукції та інших факторів, які власного вимірювача не мають. У цьому випадку запроваджують систему рангів і для аналізу використовують методи рангової кореляції.

Алгоритм дослідження має три етапи. Спочатку визначають систему рангів, порядок їх присвоєння, формують групу експертів, які розподіляють ранги. Знаходячи суму рангів для факторів, їх упорядковують. На слідуючому етапі перевіряють міру узгодженості думок експертів за допомогою коефіцієнтів рангової кореляції. Останній етап потребує установлення значущості саме коефіцієнтів рангової кореляції.

5.1. Випадок двох експертів

Приклад 6.

Працівники двох фірм оцінили вплив 10 узагальнених факторів на господарчу діяльність фірм. Найбільше значення рангу присвоювалось самому суттєвому показнику. Необхідно провести статистичний аналіз результатів опитування.

Фактори	1	2	3	4	5	6	7	8	9	10
	6	4	10	3	2	8	9	1	7	5
	5	4	9	1	3	10	8	2	6	7

де – ранги представників першої фірми; – ранги представників другої фірми.

Розв’язок.

1) Визначимо суму рангів кожного фактора, а також середнє значення рангу

Фактори	1	2	3	4	5	6	7	8	9	10
	11	8	19	4	5	18	17	3	13	12
	5,5	4,0	9,5	2	2,5	9,0	8,5	1,5	6,5	6,0

Розрахунки свідчать, що найбільш впливовими, на думку опитуваних, слід назвати 3, 6, 7 і 9 фактори, а найменш суттєвими – 8, 4, 5 і 2 фактори.

2) Перевіримо узгодженість експертів за критерієм Спірмена.

а) Знайдемо коефіцієнт рангової кореляції Спірмена за формулою 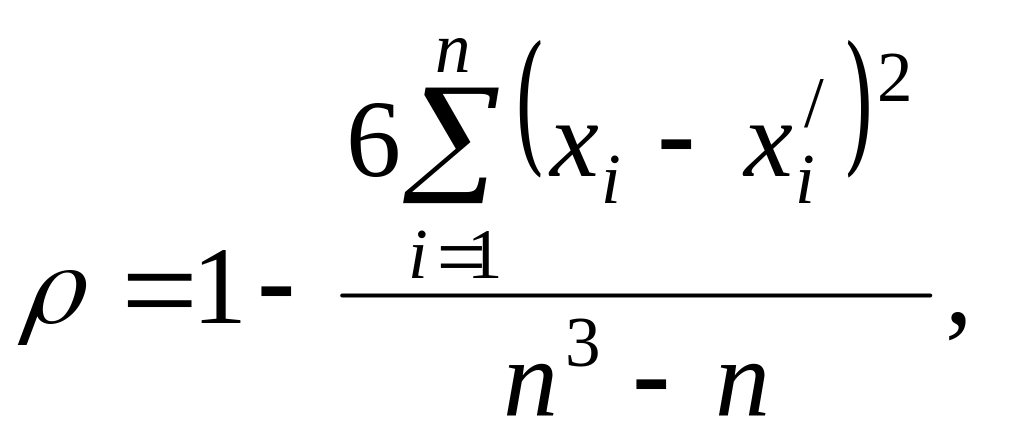(26):

(26)

У нашому випадку , тому формула (26) має вигляд

Одержане значення свідчить про високу ступінь узгодженості думок експертів відносно впливу факторів.

б) Установимо, чи буде значущим коефіцієнт Спірмена:

Критичну точку знаходимо за формулою (27):

, (27)

де знаходимо з таблиці Ст’юдента (додаток 5).

У нашому випадку , знайдене за формулою (27) дорівнює при .

Оскільки , то ранговий зв’язок факторів слід признати значним, коефіцієнту рангової кореляції і висновкам про суттєвість факторів треба довіряти.

3) Перевіримо узгодженість експертів за критерієм Кендалла.

а) Знайдемо коефіцієнт рангової кореляції Кендалла: для цього ранги першого експерта розмістимо у зростаючий послідовності, ранги другого перенесемо відповідно.

Таблиця 11 – Допоміжні розрахунки

	1	2	3	4	5	6	7	8	9	10
	2	3	1	4	7	5	6	10	8	9

Для кожного елемента другого ряду підраховуємо число рангів, що його перевершують і розташовані за ним. Підсумовуючи ці числа, одержуємо величину . У нашому випадку вона дорівнює = 8+7+7+6+3+4+3+0+1 = 39.

Коефіцієнт рангової кореляції Кендалла знаходимо за формулою (28):

(28)

У нашому випадку формула (28) має вигляд .

Розрахований коефіцієнт підтверджує висновок, зроблений раніше: між експертами існує висока узгодженість думок про вплив факторів.

б) Значущість коефіцієнта Кендалла перевіряємо, використовуючи критичну точку, яку знаходять за формулою (29):

(29)

де – критичне значення, яке знайдемо по таблиці функції Лапласа із рівності: .

У нашому випадку , тоді , тому , знайдене за формулою (29) дорівнює .

Оскільки , то ранговий зв’язок між факторами суттєвий, коефіцієнт Кендалла заслуговує довіри, а висновки про вплив факторів справедливі.