Теория вероятностей

Теория вероятностей - одна из самых молодых математических наук. Хотя первоначальные предложения теории вероятностей появи­лись еще в XVII веке, но они касались приложений ее к теории азарт­ных игр и 01 носились к случаю, когда исходов или возможных собы­тий было копечное число. В это время не было вполне ясно, являются ли вероятностные явления мерой нашего незнания всех обстоятельств каждого бросания игральной кости, или имеют особую природу. Ве­роятность - это количественная мера, укаэыващая на возможность наступления каких-либо событий. Здесь с самого начала предпола­гается, что мы не только указываем на невозможность учесть все условия при бросании игральной кости (силу броска, силу ветра и т. п.), но и па то, что принципиально невозможно указать на неизбеж­ность наступления события. Таким образом, вероятность не является мерой нашего незнания, а имеет глубокий особый смысл. При этом предполагается, что вероятность заключена между нулем и едини­цей, причем крайним точкам: нулю соответствует невероятное со­бытие; а единице соответствует неизбежное событие. Таким образом, при бросании шестигранной игральной кости все возможные выпаде­ния очков от нуля до шести оказываются равновероятными и полу­чают вероятность Задачи, которые при этом возникают, касаются совместного наступления каких-либо событий, изучения их незави­симости и т. п. Например, совместное выпадение в ходе двукратного бросания игральной кости два раза единицы получает вероятность

Такие задачи в основном решаются методами комбинаторики -науки о всевозможных комбинациях каких-либо возможностей. На­пример, коэффициент при степени к, с которым входит х^к в выраже­ние бинома Ньютона, + вычисляется методами комбинаторики. Для этого нужно сосчитать, сколько существует способов выбрать к ящичков (х-ов) из набора п ящичков (1+х). Для этого нужно выстро­ить эти п ящичков по порядку, это возможно сделать п\ способами: на первое место можно поставить любой из п ящичков, на второе - п. - 1 ящичков, и т. д. Далее нужно выбрать к первых ящичков, однако для того чтобы найти нужное число комбинаций, нужно раз­делить это число - п! на число расстановок к ящичков - fc! и на число расстановок, оставшихся не выбранными последних п - к ящичков (n — fc)!. Таким образом, число указанных комбинаций

После этого можно посчитать вероятность выбора какой-либо комби­нации ящичков.

Главная теорема, с которой отсчитывают начало теории вероят­ностей, - это закон больших чисел, который проясняет суть понятия вероятности. Закон больших^- чисел гласит, что частота происхожде­ния какого-либо события, например при бросании кости, приближает­ся к вероятности этого события и указывает скорость этого прибли­жения. Примечательно, что уже в этой теореме проводится различие между частотой события и его вероятностью. Действительно, иначе невозможно говорить о вероятности уникального события.

В повседневной жизни мы, конечно, не можем иметь дело с беско­нечным числом событий, тем не менее дальнейший прогресс в теории вероятностей связан с вероятностями в случае бесконечного числа исходов. Самым замечательным фактом здесь было открытие в нача­ле XIX века броуновского движения. Пылинки, наблюдаемые Броуном в воде, вели себя совершенно хаотическим образом, выписывая совер­шенно непредсказуемые траектории. Природа этого явления не могла быть объяснена в то время, поскольку ни атомарная теория вещест­ва, ни тепловое движение молекул не были победившими теориями.

Гениальное прозрение Больцмана, построившего свою кипети­ческую теорию газов, не было напрямую связано с попыткой понять броуновское движение, тем не менее, очевидно, имеет непосредст­венную связь с этим явлением. Кинетическая теория газов была призвана понять и объяснить природу тепловых явлений. Мы будем излагать ее в своих формулировках, широко пользуясь вероятностью.

Газ рассматривается как совокупность молекул - твердых уп­ругих шариков, движение которых описывается заданием скорос­ти каждой молекулы и ее местоположения, предполагается, что эти молекулы претерпевают упругие столкновения. Таким образом, мы имеем дело с механической системой чудовищно большой размернос­ти. Тем не менее с самого начала мы считаем, что скорости всех мо­лекул задаются при помощи вероятностных соображений, так, пред­полагается, что направления скоростей равновероятны, а величина этой скорости задается распределением вероятностей по нормально­му закону. В этом случае скорость движения молекул - случайная "еличипэ.

Случайная величина. Так называется число, значения которого (их бесконечное множество) задаются не точно, а по некоторому ве­роятностному закону - закону распределения вероятностей. Эта ве­личина как бы может принять сразу бесконечное число значений, каждое со своей вероятностью. Непрерывная случайная величина принимает значения в каком-либо интервале. Вероятностное распре­деление, задаваемое плотностью вероятностей р(1), это

г

де функция - называется нормальным, Здесь <т описывает

так называемую дисперсию этой случайной величины и для случая газа определяется температурой или сосредоточением около средней величины скорости молекул. Средняя скорость называется матема­тическим ожиданием и, очевидно, равна нулю (сколько молекул дви­жется вверх, столько же и вниз), среднее же значение квадрата ско­рости (кинетическая энергия) называется дисперсией и задает тем­пературу (рис. 14).

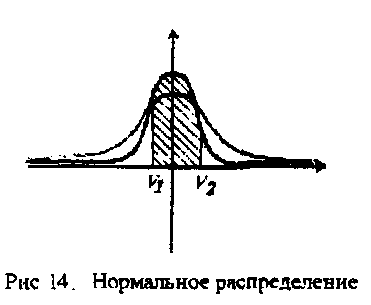
Хороший пример получается, если этой же случайной величиной мы станем описывать процесс стрельбы по цели, тогда дисперсия -это кучность стрельбы (распределение попаданий вокруг центра ми­шени) или умелость стрелка (рис. 15).

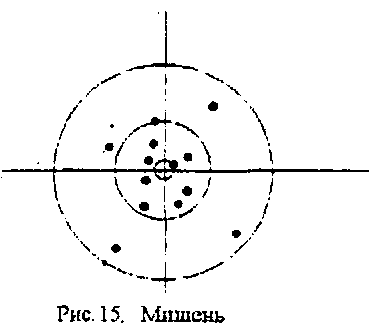
Тем не менее в таком представлении о движении молекул газа со­держится противоречие - на самом деле, если задать все положения молекул и их скорости, то, обратив скорости или изменив направ­ление времени, можно найти, из какого исходного положения нача­ла двигаться эта механическая система. Это, конечно же, не верно - все газы стремятся к равновесному распределению, и не важно, из какого положения они начали эволюционировать. Решением это­го противоречия оказывается постулат о марковости этого движения. Марковским процессом называется случайный процесс, где каждый по­следующий шаг определяется только предыдущим, но не зависит от предпредыдущего, т. е. движение молекул определяется скоростями в данный момент, но не зависит от момента до этого.

Нельзя сказать, что это абсолютно проясняет суть процессов, происходящих в броуновском движении. Оказалось, что броуновское движение, или винеровский процесс, не обладает дифференцируемой траекторией, и поэтому понятие скорости движения для него не опре­делено, даже более того, она окажется бесконечной в каждой своей точке. По самому определению, винеровский процесс (броуновское движение) W(t) обладает свойством

Первая строгая попытка аксиоматизации теории вероятностей при­надлежит А.Н. Колмогорову. Рассматривается некоторое множест­во (вероятностное пространство); все события суть подмножества данного множества; вероятность суть мера, заданная на таких под­множествах. Мера - это положительная аддитивная функция, при­нимающая значения от нуля до единицы.

Р(А + В) = Р(А) + Р(В)

К примеру, рассмотрим единичный квадрат и процесс стрельбы точ­ками в него. Тогда вероятность попадания в какую-либо подобласть этого квадрата равна площади выбранной подобласти. Хотя вероят­ность попадания в каждую конкретную точку равна нулю (рис. 16).

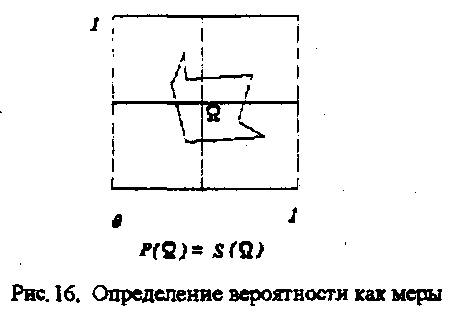
Если изменить условия задачи и поместить мишень в середину квадрата, то вероятность будет выражаться интегралом от некото­рой функции распределения, максимум которой будет располагаться в центре квадрата, и крутость ее графика определяться меткостью стрельбы, или дисперсией в терминологии теории вероятностей.

Самое значительное приложение теории вероятностей - это ис­толкование волновой функции in в уравнении Шредингера

З

десь НФ - оператор, имеющий смысл энергии. Квадрат этой комп­лексной функции имеет смысл вероятности данного состояния кван­тового объекта.

Знаменитое соотношение неопределенностей Гейзенберга

b~p&q > h

указывает на принципиальную невозможность определить точно и одновременно значения импульса р и координаты q. dp Sq - неопре­деленность импульса и координаты. Для объяснения этого явления можно использовать следующую картину. В волновом пакете, свя­занном с квантовым объектом есть волны с различными длинами-частотами, эта частота н определяет импульс р. Если захотеть ло­кализовать волновой пэкет (сумму волн) в какой-либо точке, т. е. определить координату q. то -нужно складывать волны с различными длинами - неопределенность импульса р, если захотеть определить импульс р, то придется смириться с неопределенностью координаты </, как у синусоиды, расположенной периодически но всей оси.