
Нелинейные уравнения
В последнее время были открыты динамические системы, поведение траекторий которых описывается нелинейными уравнениями, обнаруживающие странное поведение - все траектории этих систем, несмотря на полностью детерминированное поведение каждой, хаотическим образом приближаются к некоторому притягивающему множеству (аттрактору). Это множество носит название странного аттрактора. Такова, например, система Лоренца 1967:

Э та
система описывает движение так называемой
мелкой воды. Замечательно, что странный
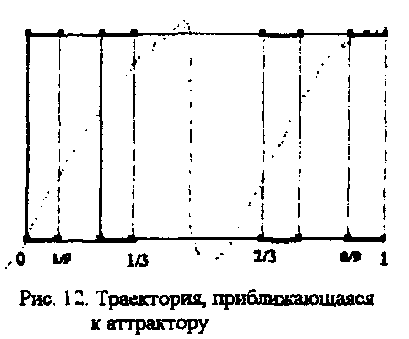
аттрактор для этой системы представляется
в виде произведения канторова множества
на единичный отрезок (рис. 12). Здесь
удивительным образом появляется
множество Кантора, по поводу самого
существования которого на рубеже веков
было сломано столько копий.
та
система описывает движение так называемой
мелкой воды. Замечательно, что странный
аттрактор для этой системы представляется
в виде произведения канторова множества
на единичный отрезок (рис. 12). Здесь
удивительным образом появляется
множество Кантора, по поводу самого
существования которого на рубеже веков
было сломано столько копий.
(Бифуркация - качественная перестройка всей фазовой картины системы.) Обнаружилось, что траектории, приближаясь к странному аттрактору, находятся как бы вблизи каждой точки этого множества, и поэтому вопрос, где же находится каждая из них в определенный момент, становится лишенным смысла. Таким образом, вопрос о предопределенности для таких траекторий становится лишенным смысла. В случае системы Лоренца в рамках теории детерминированных систем можно наблюдать превращение их в свою противоположность системы хаотические.
Для иллюстрации того, каким образом детерминированное поведение превращается в хаотическое, приведем следующее преобразование - ^преобразование пекаря». Рассмотрим единичный квадрат на плоскости. Преобразование (квадрата на себя) - растяжение по оси ОХ вдвое и сжатие по оси OY вдвое. Такое преобразование, проведенное бесконечное число раз, абсолютно детерминировано, однако проследить за поведением конкретной точки абсолютно невозможно. Все в таком поведении зависит от знаков в двоичном разложении числа - координат точки (рис. 13).

Нельзя сказать, что хаотичность в нелинейных системах была замечена в математике только после Лоренца. В работах Пуанкаре в начале XX века было открыто странное поведение самой классической системы - задачи трех тел. Задача трех тел: описать поведение системы из трех материальных тел, двигающихся по законам всемирного тяготения. Дело в том, что двигающаяся по законам всемирного тяготения пара тел, может вращаться только вокруг своего движущегося центра тяжести наподобие гантели, но уже три тела при определенном соотношении между их массами могут обнаруживать хаотическое поведение. Однако этому удивительному явлению придавалось не очень много значения, тем более удивительно, что это относится к самой фундаментальной системе - системе, движущейся по законам всемирного тяготения.
Вообще наш век можно назвать веком рождения нелинейного анализа. В различных областях стали множиться примеры нелинейных систем, которые описывают качественную перестройку поведения системы: возникновение новых структур; катастрофические изменения (тюремные бунты), возникла даже новая теория с громким названием теория катастроф. Методы исследования таких систем - системы Лоренца, социальных систем - опираются на теорию бифуркаций. Бифуркация - качественное изменение фазового портрета при прохождении параметра в системе через какой-либо бифуркационный порог. Например, система, обнаруживающая фокус в точке О, превращается в систему с седлом в этой точке, иногда такое поведение можно назвать катастрофическим, но, конечно же, не всегда. Математически теория бифуркаций опирается из разложение по малому параметру в окрестности особого значения, т. е., конечно, на линейную теорию.
В последнее время к этим явлениям привлечено значительное внимание различных специалистов - от философов до физиков. Есть надежда, что изучение таких систем даст ключ к пониманию развития из простых систем сложных и глубоко структурированных. К примеру, в какой момент и каким образом масса клеток развивающегося плода превращается в живой организм со специализацией своих частей.
Еще одно замечательное применение нелинейного анализа - теория солитонов. Явление отдельной уединенной волны было замечено и описано еще в 1834 году Дж.С. Расселом, который наблюдал ее в канале, соединенном с Темзой.
В настоящее время эта теория превратилась в достаточно обширную и разработанную теорию - теорию солитонов, т. е. теорию волн, которые ведут себя как частицы. Эти волны имеют ограниченную область, в которой они наблюдаются, они могут особым образом взаимодействовать между собой, преодолевать преграды и т. п., что характерно для частиц. Такое математическое явление, как соли-тон, наполняет новым пониманием корпускулярноволновую теорию
Э
вещества, света. Тем более что уравнения, в которых наблюдаются солитонные решения, это уравнения Шредингера.
то уравнение, основное в квантовой теории, мы обсудим ниже в связи с вероятностной интерпретацией квантовой механики.
