3.5.4 Плоский згин

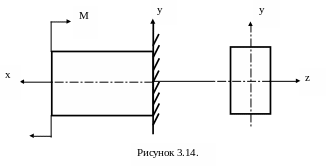При плоскому згині (рис.3.14) у стержні з’являються дотичні та нормальні напруги. Але неврахування дотичних напруг при розрахунках дає похибку біля 3%. Тому умови міцності при згині можна записати у вигляді:

, (3.21)

де - допустимі напруги при згині.

Прогин (деформацію) балки можна знайти наближено із диференціального рівняння зігнутої осі балки.

, (3.22)

де М_x – згинальний момент по довжині балки.

Приклад: Знайти максимальний прогин балки (рис.3.15), що знаходиться під дією рівномірно розподіленого навантаження інтенсивністю q.

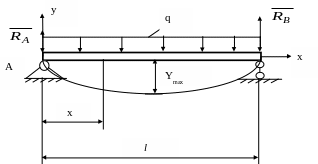
Рисунок 3.15.

Балка симетрична, і тому максимальний прогин буде у її середині. Знайдемо згинальний момент для характерного перерізу балки

,

якщо , то .

Використаємо диференційне рівняння (3.22)

.

Інтегруючи двічі, отримаємо:

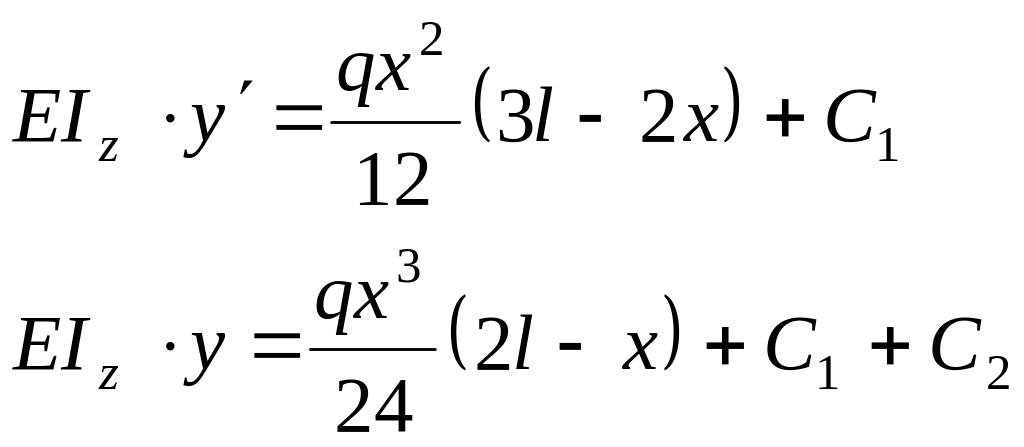(3.23)

Граничні умови:

при ;

при .

Тоді .

Рівняння (3.23) набуває такого вигляду:

. (3.24)

При . (3.25)

Із виразу (3.24) при умові (3.25), отримаємо:

.

3.6 Завдання ргр з опору матеріалів ом.1 Центр ваги пластини

Визначити центр ваги пластини (рис.3.17). дані для розрахунку в табл.3.1 приведені в метрах.

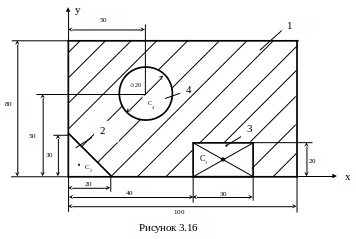
Приклад: Знайти центр мас поперечного перерізу, що показаний на рис.3.16. Розміри приведені в міліметрах.

Центр мас поперечного перерізу знаходимо із виразів:

, (3.26)

де: - площа k-ї фігури; - координати центра мас k-ї фігури.

Поперечний переріз розглядаємо як прямокутник 1 розмірами 10080мм з якого вирізали трикутник 2, прямокутник 3 та коло 4.

Визначимо площі та координати центрів мас тіл 1,2,3,4.

Таблиця 3.1

Ва-рі-ант	C	d	C1	C2	d1	d2	xк	yк	Xn	yn	h	b	R
1 2 3 4 5	0.2 0.3 0.4 0.5 0.6	0.7 0.2 0.3 0.4 0.5	- 0.1 - 0.2 -	0.1 - 0.15 - 0.2	- 0.05 - 0.2 -	0.2 - 0.3 - 0.1	0.02 0.02 0.3 0.1 0.3	0.04 0.02 0.25 0.1 0.4	0.1 0.15 0.05 0.2 0.1	0.4 0.1 0.05 0.2 0.2	0.2 0.05 0.1 0.1 0.2	0.05 0.1 0.2 0.2 0.1	0.01 0.01 0.02 0.05 0.1
6 7 8 9 10	0.7 0.8 0.7 0.6 0.5	0.6 0.7 0.6 0.5 0.4	0.3 - 0.2 - 0.1	- 0.3 - 0.2 -	0.4 - 0.1 - 0.05	- 0.4 - 0.25 -	0.5 0.6 0.3 0.2 0.3	0.4 0.5 0.2 0.2 0.3	0 0.1 0.4 0.3 0	0 0.2 0.4 0.3 0	0.3 0.2 0.3 0.2 0.15	0.1 0.2 0.1 0.1 0.2	0.1 0.1 0.2 0.15 0.05
11 12 13 14 15	0.4 0.3 0.2 0.8 0.7	0.3 0.5 0.4 1.0 0.9	- 0.1 - 0.4 -	0.2 - 0.05 - 0.3	- 0.2 - 0.05 -	0.1 - 0.2 - 0.2	0.1 0.2 0.1 0.6 0.5	0.1 0.3 0.1 0.7 0.7	0.2 0 0.1 0.1 0.5	0.25 0 0.2 0.1 -	0.1 0.1 0.05 0.2 0.4	0.1 0.2 0.1 0.3 0.2	0.1 0.1 0.05 0.1 0.1
16 17 18 19 20	0.6 0.5 0.4 0.3 0.4	0.8 0.7 0.6 0.5 0.4	0.2 - 0.1 - 0.05	- 0.2 - 0.1 -	0.3 - 0.2 - 0.1	- 0.4 - 0.2 -	0.2 0.3 0.2 0.2 0.1	0.3 0.5 0.2 0.2 0.1	0.5 0 0.3 0 0.3	0.5 0 0.1 0 0.3	0.1 0.2 0.2 0.1 0.1	0.1 0.3 0.1 0.2 0.1	0.1 0.1 0.2 0.1 0.1
21 22 23 24 25	0.9 0.8 0.7 0.6 0.5	0.7 0.6 0.5 0.4 0.3	- 0.3 - 0.2 -	0.3 - 0.3 - 0.1	- 0.1 - 0.1 -	0.1 - 0.1 - 0.05	0.5 0.1 0.5 0.1 0.4	0.4 0.1 0.4 0.1 0.2	0 0.6 0 0.4 0	0 0.5 0 0.3 0	0.2 0.1 0.2 0.1 0	0.3 0.2 0.2 0.1 0	0.1 0.1 0.1 0.2 0.1
26 27 28 29 30	0.4 0.3 0.8 0.7 0.6	0.2 0.5 0.6 0.5 0.4	0.1 - 0.3 - 0.2	- 0.05 - 0.3 -	0.05 - 0.2 - 0.1	- 0.1 - 0.1 -	0.1 0.2 0.1 0.5 0.1	0.1 0.4 0.1 0.4 0.1	0.3 0 0.5 0 0.5	0.25 0 0.4 0 0.3	0.05 0.1 0.2 0.3 0.1	0.1 0.1 0.3 0.3 0.1	0.2 0.2 0.1 0.1 0.2

Тіло 1:

Тіло 2:

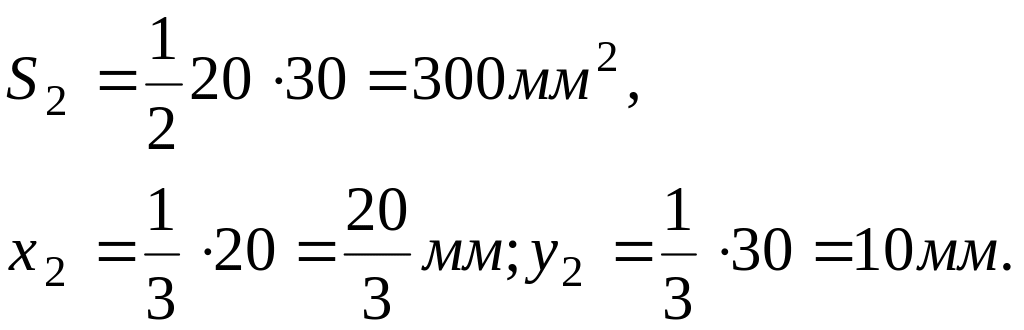
Тіло 3:

Тіло 4:

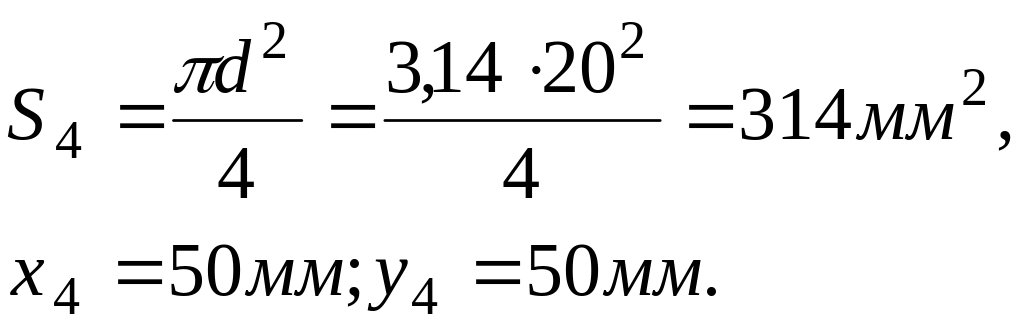
На підставі виразів (3.26) знаходимо центр ваги поперечного перерізу, враховуючи, що тіла 2,3,4 вирізали із прямокутника. Тобто площі тіл 2,3,4 необхідно враховувати з від’ємним знаком

Таким чином: