1 0. Устойч-ть равнов. Сост-й. Крит-ии наличия равнов-я и его уст-ти в разл. Случаях. Огранич-я, налаг. На измен-я пар-ров устойчиво равнов. Тд-с-м. Положит-ть cv и βТ.
Е
сли
вывести с-му из сост-я равнов-я путем
беск-но малого измен-я ее пар-ров при
заданном огр-ии на их измен-е, то с-ма
сама возвращ в равнов. сост-е. Различ.
осн. (стаб.) равнов. сост-е от менее стаб.
(метастаб.) равнов. сост-е. Самому уст.
сост-ю соотв. миним. знач-е поте
н
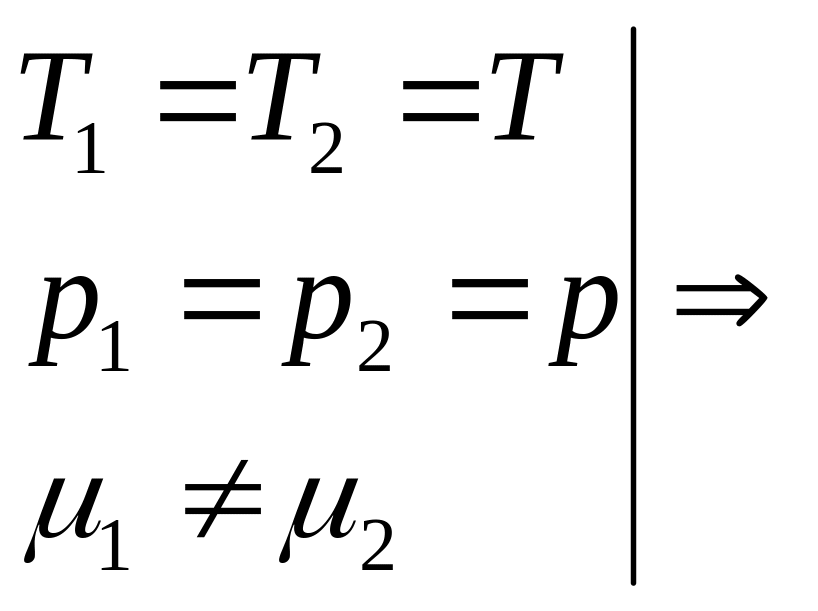
ц.
эн.Сильное возмущ-е разруш. метастаб.
сост. Аналог. образом в ТД всегда м. указ.
ТД-ф-цию, кот. при уст-м равнов-ии им.
экстремум. и миним. знач-е в осн. равнов.
сост-ии. Изолир. с-ма: Smax
соотв. сост-ю равнов-я, и это сост-е
уст-во, т.к. согласно пост. равнов-я с-ма
прих. в равнов. сост-е. При любом отступл-ии
от равнов-я числ. знач-е энтр. уменьш. xi
– равнов-е; S(xi)-S(x0)
≤ 0; ∆S ≤ 0 – мат. выраж-е,
кот. соотв-т равнов. сост-ю с-мы
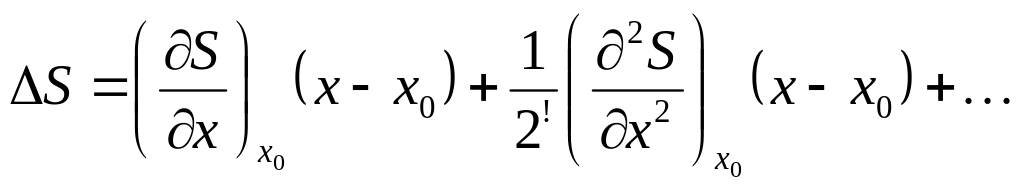Но
S’=0 и S’’=0
след-но S’’’=0(д.б.)
и S’’’’<0
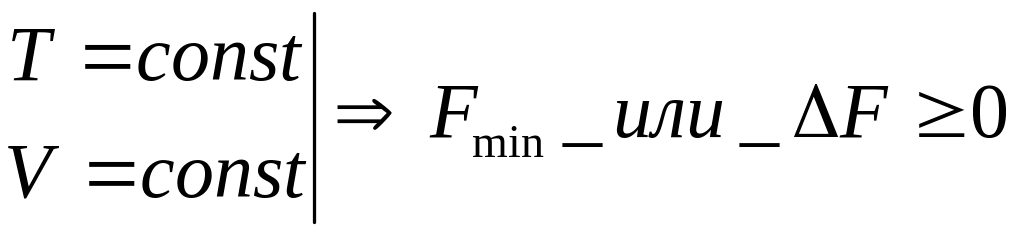
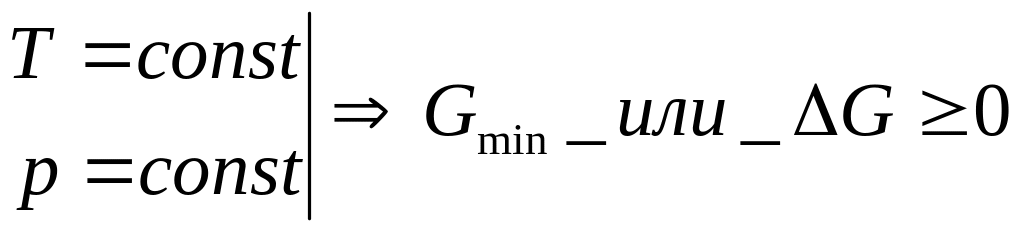dU≤TdS-pdV;
U, S, T,
p, V – входящие
вел-ны. Им. равнов. ТД-сост-е, кот. хар-ся
пар-рами (U1, S1,
V1, T1,
p1). Приведем с-му
изотермо-изобарически в неравнов. сост-е
с пар-рами (U2, S2,
V2, T1,
p1). Допускаем, что
в окресностях от нач. сост-я им. др.
равнов. сост-е с пар-рами
(U2,
S2, V2,
T2, p2).
Сделаем изотермо-изобарич. переход в
сост-е (U1, S1,
V1, T2,
p2). Всякое отклон-е
от равнов-я прив. к тому, что ТД-пот-л
возраст. ∆G ≥ 0.
G=U-ST+pV;
(U2-S2T1+p1V2)
– (U1-S1T1+p1V1)
≥ 0
(U1-S1T2+p2V1)
– (U2-S2T2+p2V2)
≥ 0
(U2-U1)
– T1(S2-S1)
+ p1(V2-V1)
≥ 0 │ +
– (U2-U1) + T2(S2-S1) – p2(V2-V1) ≥ 0 │ (S2-S1)(T2-T1) – (V2-V1)(p2-p1) ≥ 0 или ∆S∆T – ∆V∆p ≥ 0 В получ. выр-ии стоят множ-ли, кот. соотв. разности вел-н д/двух близких равнов. сост-й. Д/равнов. устойч. с-м измен-я пар-ров в равнов. проц. не м.б. любыми, они д. удовл. получ. нерав-ву.
О
пираясь
на получ. нер-во м. прийти к огранич-ям
отдел. пар-ров. Изохорич. переход, ∆V=0:
∆SV∆TV
≥ 0
CV
–изохорич.Изотермич. переход, ∆Т=0: –
∆VT∆pT
≥ 0
При
отриц. сжим-ти увел-е давл-я прив. к
увелич. объема. В свою очередь увел-е
объема прив. к дальн. увел-ю давл-я и т.д.
С-ма идет вразнос. Рассм. случаи явл.
примером правила ЛаШателье-Брауна: при
внеш. возд-ии всякая уст. с-ма отвечает
реакцией, напр-й против внеш. возд-я или
стремящейся ослабить д-е внеш. сил.
11. Равнов-е в 2-фазн. С-ме. Усл-я наличия равнов-я. Хим. Пот-л как пар-р, определяющий возм-ть и напр-е диффузии. Кривая равнов-я двух фаз.
Ф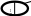
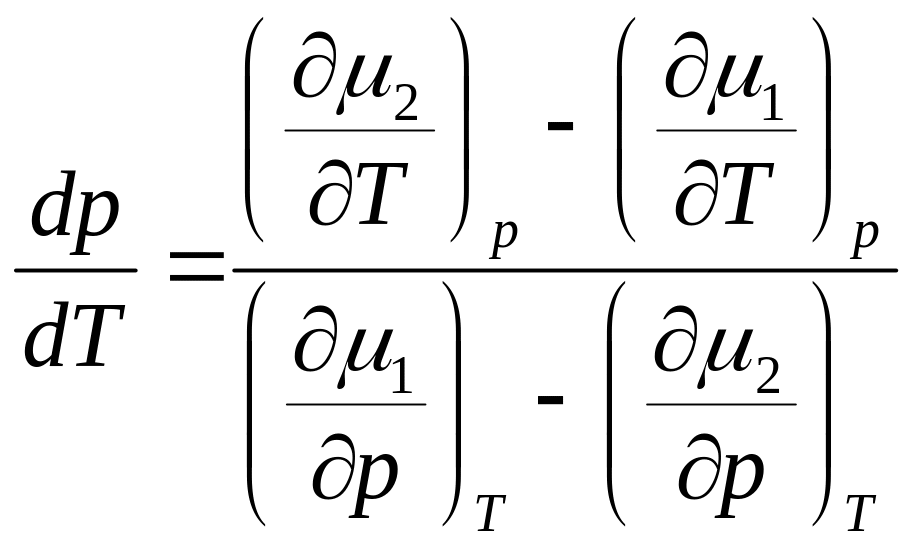аза
– физически однор. часть гетерогенной
с-мы, отдел. от др. частей четко выраж.
границей раздела.
– [адиабатич.
оболочка] (тепло не поступает)
U,
V – const На
границе раздела скачком измен. разл.
пар-ры. В теор. рассужд-х счит., что граница
– плоская пов-сть. С-мы равнов., но м/у
с-мами равнов-я нет. Т.к. равнов-я нет, то
с-мы м. возд-ть др. на др. М/у ними м. происх.
Т-обмен, обмен ч-цами за счет диффузии.
О
говорки:
● адиаб. обол.; ● с-мы – простые. Д/всей
с-мы вцелом ∆S ≥ 0; S=S1+S2;
∆S=∆S1+∆S2.
С-мы остаются равнов. dU=TdS-pdV+μdN
U=const
U1+U2=const
dU1=-dU2
dV1=-dV2
N=const
dN1=-dN2
(Складываем
I и III ф-лы)
dU1,
dV1, dN1
≠ 0, т.е. рав-во нулю ∆S
м.б. только при
T1=T2,
p1=p2,
μ1=μ2. T1=T2
обеспеч. термич. равнов-е; p1=p2
обеспеч. механич. равнов-е; μ1=μ2
дает дифф. рвнов-е
Возможна диффузия,но
в каком напр-ии она идет?
dN1<0
μ2-μ1<0 μ1>μ2
– ч-цы перемещ. из мест с меньшим μ в
места с большим.
Обратим вним., что
хим. пот-л м.б. выч., если изв. т-ра и давл-е
в люб. прост. с-ме. μ=μ(T,V,N);
μ=μ(p,T);
p=p(T,V,N);
V=V(p,T,N);
μ1(p,T)
≥ μ2(p,T).
Это откр. возм-сть рассм. ситуацию
геометрич., μ1(p,T)
и μ2(p,T)
– изв.:
μ1(p,T)=μ2(p,T)
при p,T обе
фазы равнов. Возм-но мн-во точек равнов-я
фаз, они б. лежать на к.-то кривой p=p(T)
– кривая равнов-я двух фаз.
12. Ур-е Клап.-Клауз. Вывод ур-я. Анализ возм. решений.
μ1(p,T)
и μ2(p,T);
p(T); μ1(p(Т),T)
и μ2(p(Т),T)←Продифф.
тождество от т-ры:
- позволяет найти кривую равнов-я
В
числ-ле стоит разность энтропий одной
и той же массы в-ва, однако в одном случае
в-во нах. в одной фазе, а в др. случае –
в др. фазе. Но при одном p
и T, при кот. осущ. переход.
Знак ̃ означ., что берутся уд. вел-ны.
ΔS̃=S̃2-S̃1=q/T;
q – тепловой эффект
процесса (из расчета на 1 моль в-ва), кот.
наз. скрытой теплотой перехода в-ва из
одной фазы в др.
← ур-е
Клапейрона-Клаузиуса
Если добавлять
тепло,то одна фаза б.увлич.,др.–уме
н
ьш.,
и наоборот (если отнимать Q),
и так до полного разруш-я одной из фаз.
А, В – неранов. сост-я, одна из фаз б.
увелич., др. – уменьш., пока не ост. одна
фаза (если поддерживать свойственные
T и p).
- обычно
λ>0 T>0
13. Ос-сти ФП м/у агрег. сост-ми одного и того же в‑ва. Тройная точка. Критич. сост-е. Метастаб. однофазные сост-я в-ва. Изотермы перехода ж-сти в пар. Изотермы Ван-дер-Ваальса.
О
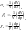бычно
агрег. сост-е одного и того же в-ва
образует одну фазу в с-ме. Агрег. сост-й
– три, фзовых м.б. больше.
↑ два ур-я с двумя неизв. м.
им. реш-я. Т.е. три фазы м. сосущ-ть в
равнов-ии др. с др. в к.-то точке на пл-сти
p, T – тройная
точка (напр., воды). 4 фазы одного и того
же в-ва не м. сосущ-ть вместе – одна
исчезнет.
← все графики начин. с
тройной точки. К – критич. точка прямой
ж-сть–пар. На кривой Т-Ж появл. новые
тройные точки. Наличие тройной точки и
критич. точки есть первые ос-сти ФП м/у
агрег. сост-ми. Критич. точка им. место,
т.к. при критич. давл-ии и т-ре пропад.
различие м/у ж-стями и газами. Все их
физ. св-ва сравнив., исчез. граница
раздела, поверхн. натяж-е стан. равно 0.
Почему нет критич. точек на кривых Т-П,
Т-Ж? Дело в том, что в т.т. им. опред. порядок
в распол-ии ч-ц. Порядок либо есть, либо
его нет. Поэтому св-ва т.т. не м.б. непрер.
образом продолжены к жидкому или парообр.
сост-ю. В Ж и П порядка среди ч-ц нет.
Третья ос-сть ФП – наличие метастаб.
сост-й. Они м.б. м/у любыми агрег. сост-ми.
Метастаб. сост-е – однофазное равнов.
сост-е некот. фазы в области, где она
неуст., а уст. др. фаза. Напр., вода по
правую стор. кривой Ж-П. Они не явл. стаб.,
малейшее возмущ-е ведет к выводу из
метастаб. сост-я. Дело в том, что новая
фаза (при ФП) возник в толще старой в
виде мельч. зародышей. Если усл-я благопр.,
то зародыши растут и осущ. ФП. В противном
случае зародыши, раз возникнув, исчезают,
ФП не произв.
Е
сли
заданы р и Т, то м. найти удел. объем
Ṽ=Ṽ(р,Т).
Двухфазная с-ма м.б. опред. по объему,
если изв. уд. объемы обеих фаз.
Ṽ1–жид-ть,Ṽ2–уд.об.газа.V=mжṼ1+mгṼ2;
m=mж+mг=const.
Каждой точке на диагр. р(Т) соотв. прямая
линия, целый отрезок на диагр. р(V).
mṼ1 ≤ V
≥ mṼ2. По внутр.
устр-ву газовая и жидкая фазы им. общее:
б/порядок в распол-ии и движ-ии ч-ц.
Поэтому различие м/у в-вом в обеих фазах
скорее колич., чем кач. Это позв. г. и ж.
фазы изучать вместе, опис-ть их одним
ур-ем сост-я.
←
реальные
изотермы
Две фазы м. отличить др. от
др. только при т-ре, меньшей крит. За Ткр
в-во нельзя назв. ни ж-стью, ни газом. В
обл. справа от дуги КВ при Т<Ткр
в-во обычно плохо подчин. ур-ю Бойля-Мариотта.
Все эти данные относ. к равнов. сост-ям.
Д/того, чтобы делать сопоставл-е, надо
выделить точки А и В. По Максвелу: площадь
бугорков д.б. одинак. Ур-е ВдВ двухфаз.
сост-й. не выдает, опис. лишь одноф.
сост-я. АС, DB: метастаб.
CD, (∂р/∂V)Т>0:
нестаб. сост-е. АКС: м.б. уст. двухфаз.
сост-я и метастаб. одноф.
CKD:
им. уст. двухфаз. сост-я, устойч-х однофазных
нет.
DKB: им. уст. двухфаз.
сост-я, и метауст. одноф. типа переохл.
газа. Справа от КВ: одноф. сост-я. За Ткр
(///) уст. однор. сост-я. Чем выше т-ра, тем
ближе ход изотерм к гиперболе
Бойля-Мариотта. Точка К: (∂р/∂V)T=0,
(∂2p/∂V2)=0
– точка перегиба.
14. Хар-ные ТД-коэф-ты α, β и γ. Связь αр, βТ и γV.
p=p(V,T); V=V(p,T)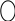
-
объемный коэф-т расшир-я
- сжимаемость
(хар-зует упругие св-ва с-мы по отнош. к
всестор. сжатию или расшир-ю)
- коэф-т
термич. измен-я эн.
Равнов.
(pVT)-с-ма: ● внешний пар-р
V;
●
-
изобарич. коэф-т термич. расшир-я
●
- изотермич. сжимаемость
●
-
изохорич. коэф-т термич. измен-я давл-я
Вычисление αр,
βТ и γV д/ид.
газов:
Ф-ла связи м/у
αр, βТ и γV:
р=р(V,T);
p=const;
dp=0:
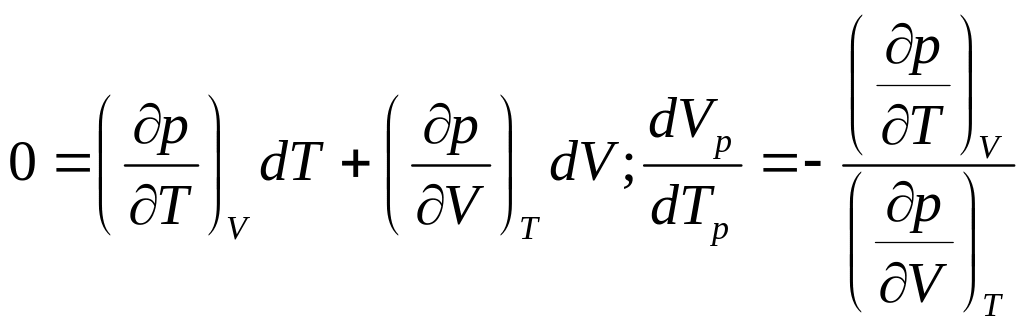p=p(V,T);
V=V(p,T):
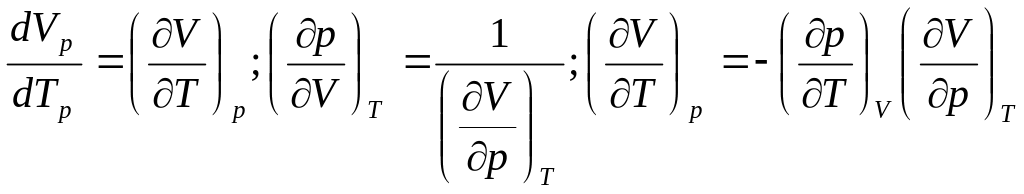αp=γVpβT