5. Переход от т.Карно к осн форм-ке 2го нач тд. Рав-во–нер-во Клаузиуса. Энтропия. Осн форм-ка 2го нач.

Q ₁ ≥ 0, Q₂ ≥ 0 – арифм. вел-ны. Будем опред. знак тепла по отнош. к маш. Карно: Q₁ ≥ 0, Q₂ ≤ 0 – алгебр. вел-ны. Кол-во тепла, отнес. к темп-ре, при кот. оно получ., наз. привед. теплотой. Сумма привед. теплот д/маш. Карно меньше либо равна 0. Знак «=» д/обрат. маш. Пусть маш. раб. по произв. циклу. Разобъем его изотермами и адиабатами – пол. мн-во циклов Карно. ← д/нашего цикла. 1) Внеш. контур нашей с-мы циклов стрем. к кривой исх. цикла; 2) Слагаемое д/внут. изотерм выпад. из расчета. δQ_k= - δQ_k+1 Если бы циклы б. обрат., компенсация б. бы точная; а в общ. случае – только в пределе. В рез-те получ. сумму, где суммир-е по внеш. контуру: - рав.-нерав. Клауз.Рав.-нерав. Клауз. явл. более широкой форм-кой 2_го нач. ТД, чем т.Карно. Его м. исп. д/любых круговых проц.

П рим. рав-во Кл. к обратному циклу. Данное соотн-е справ. д/люб. замкн. цикла. ↑ интеграл не зав. от пути интегр-я. - энтропия. Т.о. Кл. пришел к выводу, что сущ. новая ф-ция сост-я с-мы, энтропия S, чье измен-е в равнов. проц. равно теплоте. Рассм. случай, когда цикл явл. необр.: Измен-е энтр. в неравнов. проц. всегда больше привед. теплоты (распр-е пон. энтр. на все проц.). Общая форм-ка 2^го нач ТД: сущ-т ф-ция сост-я – энтропия; измен-е энтр. в равнов. проц. равно прив. тепл.; измен-е энтр. в неравнов. проц. больше прив. тепл.

6 . Некот. След-я из 2го нач. Тд. Др. Форм-ки 2го нач. Как след-я из осн. Обоснование тд-шкалы темп-р.

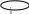
О сн. форм-ка 2^го нач ТД: сущ-т ф-ция сост-я – энтропия; измен-е энтр. в равнов. проц. равно прив. тепл.; измен-е энтр. в неравнов. проц. больше прив. тепл. Эта форм-ка явл. осн., т.к. напрямую прим. к люб. с-ме. Др. форм-ки м.б. получ. из осн. Из осн. форм-ки м. получ. след. выводы: 1) S – есть ф-ция сост-я, в каждом сост-ии S свое и только одно; 2) Энтр. опред. с точн. до аддит. слаг. (нельзя получ. абс. знач-е): 3) S – явл. аддит. ф-цией, т.е. д/с-мы из двух частей: S_I=S_I+S_II. Покажем, что форм-ки Кл. и Кел. след. из этой форм-ки. ΔS=ΔS_I+ΔS_II. Доп.: каждая подс-ма равнов., но с-ма вцелом неравнов. т.к. с-ма вцело не получ. и не отд. тепло; это возм., если Т₁>Т₂ (если тепло само собой б. перех. от гор. тела к хол.). Рассм. форм-ку Кел. Доп.: Q=A ΔS>0 (т.к. с-ма не получ. и неотд. тепло) ΔS=ΔS₁+ΔS₂+ΔS₃ ΔS₂=0 (маш. Карно возвр. в исх. сост-е) ΔS₃=0 (над телами сов.только внеш. тело работа, внут. сост-е 3^го тела не мен.) - пришли к противоречию, т.к. ΔS>0 Осн. форм-ка позв. получ. и др. следствия – новые форм-ки 2^го нач. ТД. Напр., д/замкн. с-мы ΔS ≥ 0, где «=» относ. к равнов-ю. d S≥0 (возр-е энтр. в замкн. с-ме) , если проц. адиаб., то δQ=0 dS ≥ 0 S возр. при адиаб. проц.Не м. гов. о максим. энтр.; S всегда монотонно растет. Физ. смысл: энтр. – есть физ. вел., кот. указ. степ. близ. с-мы к равнов-ю и напр-е дальн. эвол. – новый фунд. з-н прир. Вывод Кл. о тепл. смерти Всел.: рано или поздно с-ма прих. к равнов. сост-ю. Но пробл.: не ясно какая Всел. Набл-я показ., что Всел. крайне далека от равнов-я. Приход к равнов-ю не означ. прекращ-е внут. движ-я в с-ме. Это движ-е в изв. мере обесценив., его уже нельзя исп-ть д/сов. работы. Приор. роль в ТД им. две ф-ции: внут. эн. U и энтр.S. В замкн. с-ме м.б. организованные стр-ры, в кот. в отдельности взятых S м. ↓ или ↑. Прим.: от Солнца мы получ. Q: Т ≈ 6000К, dS=δQ/T. А сама Земля излуч. Q’: dS’=δQ’/T’, Т’ ≈ 300К. dS<dS’ → на Земле возм. организ. стр-ры.

Т – эмпир. т-ра, отсчит. по шкале Кел. и измер. по терм-ру с ид. газом в кач-ве раб. в-ва. М. док-ть, что именно эта т-ра б. совп. с абсол.

Тела I-III поддержив. в сост-ии, что их Т_1,2,3=const. Данные тела служат хол-ками или нагр-ми д/маш. Карно. Отрегулируем так, чтобы кажд. тело из этой цепочки: сколько Q A₁=Q₁-Q₂ получ., столько же и отдав. Q₂=Q₃. Пусть все маш. Карно за цикл соверш. одну и ту же работу А₁=А₂. Пусть все маш. явл. равнов., обратимыми. Согласно т.Карно: ↓↓↓ A₂=Q₃-Q₄ Это рав-во м.б. достиг. подбором тел хол-ка и нагр-ля. По какому признаку м. судить, что это рав-во достиг.: при однокр. срабатыв-ии всех маш. хол-ки и нагр-ли верн. в исх. сост-е и все маш. произв. одинак. работу. Если Т₁=12, Т₂=11, Т₃=10, то эти цифры явл. абсол. при выбранной шкале т-р, поск-ку они получ. путем измер. работы, а не ч/з показания к.-л. терм-ра. Открыв. возм-сть постр-я абс. шкалы т-р. Кроме того 2^е нач. ТД указ. на наличие абс. нуля т-р. Т<0 – не м.б.; η>1 – запр. 1^м нач. ТД. Т.о. сущ. абс. «0» т-р. Если Т₁ ≠ 0, Т₂=0 → Q₂=0. Значит, если мы постр. тепл. маш. по циклу Карно с хол-ком, им. нулев. т-ру, то получим устр-во, в кот. взятое у тела тепло Q нацело превр. в работу А. В данном случ. форм-ка Кел. оказ. неверной. Если неверна одна форм-ка, то неверны и др. Оказ., что 2^е нач. ТД противор. само себе. Выход из полож-я дан Нерстом в кач-ве 3^го нач. ТД: запрет сущ-я тел с Т=0К. Этот факт не след. из 1^го и 2^го нач. ТД. Он предст. собой самост. полож-е, б/кот. ТД неполна.