Приклад розрахунку типового варіанту задача №1 Розрахунок показників надійності невідновлювальної системи часу інтенсивності відмов елементів

Вихідні дані:

1. Структурна схема системи:

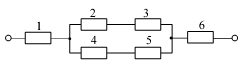
2. Інтенсивність відмов елементів системи за час t:

№ елемента	1	2	3	4	5	6
λ•10-3, год-1	1,2	2,2	3,3	4,5	2,7	0,9

t =120 год

Визначити:

1. Імовірність безвідмовної роботи системи P_с(t) за заданий час t.

2. Щільність ймовірності відмови системи f_с(t) в момент часу t.

3. Імовірність появи відмови Q_с(t) за заданий час t.

Розв’язок:

На початковому етапі розрахунків приймемо P(t)=P.

Так як елементи Р₂ і Р₃ з’єднані послідовно, то загальний вираз ймовірності їх безвідмовної роботи має вигляд:

Р₂₃=Р₂•Р₃. (1.1)

Елементи Р₄ і Р₅ також з’єднані послідовно, тобто, загальний вираз ймовірності їх безвідмовної роботи має вигляд:

Р₄₅=Р₄•Р₅. (1.2)

Загальний вираз ймовірності безвідмовної роботи для елементів Р₂ – Р₅ приймає вигляд:

Р₀₁=1-(1-Р₂₃)• (1-Р₄₅)=Р₄₅+Р₂₃-Р₄₅•Р₂₃. (1.3)

З урахуванням (1.1) і (1.2) вираз (1.3) приймає вигляд:

Р₀₁=Р₂•Р₃+ Р₄•Р₅-Р₂•Р₃•Р₄•Р₅.

У результаті перетворень отримаємо наступну загальну структурну схему системи (рис.1.1):

Рисунок 1.1 – Узагальнена структурна схема системи

У результаті ймовірність безвідмовної роботи системи Р_с=Р_с(t) буде:

(1.4)

Оскільки Р=P(t)=е^-λt, то P_с(t) приймає наступний вигляд:

Вираз густини імовірності відмов f_с(t) із врахуванням, що

(1.6)

має вигляд:

Вираз для визначення імовірності появи відмови Q_с(t) має наступний вигляд:

(1.8)

Підставивши вихідні дані у вирази (1.5), (1.7) та (1.8) отримаємо:

1. Імовірність безвідмовної роботи системи за заданий час P_с(t)=0, 56.

2. Густина імовірності відмови системи f_с(t) в момент часу t: f_с(t)=3,6×10^-3 год^-1

3. Імовірність появи відмови Q_с(t) за заданий час t: Q_с(t)=0,44

Задача №2 «Розрахунок показників надійності невідновлювальної системи з постійними в часі інтенсивностями відмов елементів»

Вихідні дані:

1. Структурна схема системи:

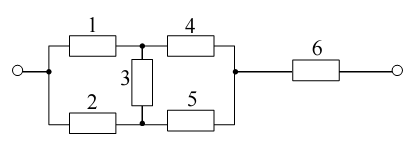
2. Інтенсивність відмов елементів системи за час t:

№ елемента	1	2	3	4	5	6
λ•10-3, год-1	1,2	2,3	3,0	2,8	2,8	0,3

t =120 год

Визначити:

1. Імовірність безвідмовної роботи системи P_с(t) за заданий час t.

2. Середнє напрацювання до відмови Т₀

3. Частоту відмов f_с(t).

4. Інтенсивність відмови системи λ_с.

Розв’язок:

1. Для знаходження імовірності безвідмовної роботи системи скористаємося методом розкладання структури відносно базового елемента. Метод базується на теоремі про суму ймовірностей несумісних подій.

В якості базового елемента вибираємо 3й.

Відповідно до теореми маємо дві несумісні події:

а) Базовий елемент знаходиться в працездатномуздатному стані, тобто Р₃=1 і його замінюємо перемичкою.

Тоді структурна схема набуває наступного вигляду (рис. 2.1):

Рис. 2.1 – Структурна схема системи, коли базовий елемент знаходиться в працездатному стані

Для даної системи ймовірність безвідмовної роботи Р_с1(t) складатиме:

(2.1)

б) базовий елемент знаходиться в стані відмови, тобто Р₃=0 і його замінюємо розривом.

Тоді структурна схема системи набуває наступного виду (рис. 2.2):

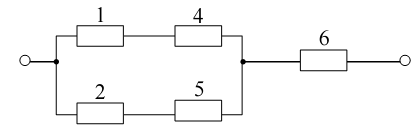
Рисунок 2.2 – Структурна схема системи, коли базовий елемент знаходиться в непрацездатному стані

Для даної системи імовірність безвідмовної роботи Р_с2 (t) становитиме:

(2.2)

Імовірність безвідмовної роботи вихідної системи визначається за формулою:

де Р_бе – імовірність безвідмовної роботи базового елемента;

Q_бе – ймовірність відмови базового елемента;

Р_с1|_Рбе - ймовірність безвідмовної роботи першої допоміжної структури;

Р_с2|_Qбе - імовірність безвідмовної роботи другої допоміжної структури.

Оскільки в якості базового прийняли 3й елемент і Q(t)=1-P(t) маємо:

(2.3)

Підставивши вихідні дані, отримаємо:

2. Визначимо середнє напрацювання до відмови, скориставшись формулою :

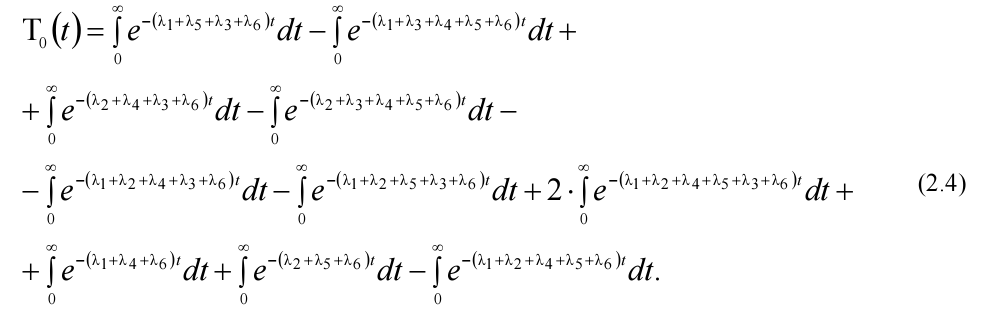
Оскільки P(t)=e^-λt , то Т=1/λ. В результаті отримаємо:

Підставивши вихідні дані, отримаємо Т₀=683,334 год

3. Інтенсивність відмов системи:

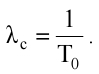(2.6)

Підставивши вихідні дані, отримаємо

λ_с=1,463×10^-3 , год^-1

4. Частота відмов системи:

(2.7)

Підставивши вихідні дані отримаємо

fc(t)=1,228×10^-3год^-1