2.2. Расчет на жесткость стержня постоянного сечения.

Д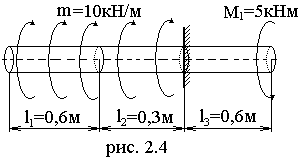ля стержня постоянного сечения (рис. 2.4) необходимо построить эпюру углов закручивания и из условия жесткости найти искомое значение диаметра стержняd. Материал стержня – сталь,G=80Гпа.

2.2.1. Построение эпюры углов закручивания.

Разобьем стержень на участки ABиBC(рис. 2.5). В пределах каждого участка возьмем произвольные сеченияz₁иz₂соответственно.

Из условия равновесия определим момент в заделке:

Участок AB(0z₁l₁+l₂):

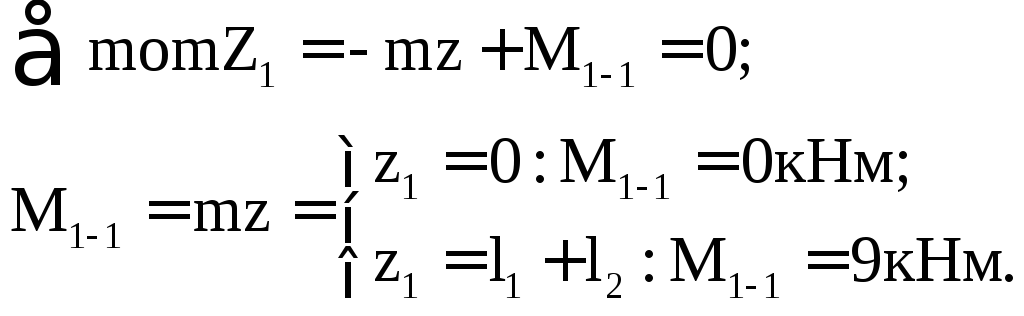
Участок BC(l₁+l₂z₂l₁+l₂+l₃):

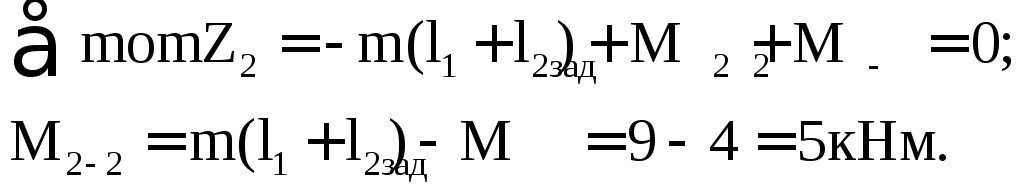
Находим углы закручивания в долях 1/GI_p.

На участке АВ:

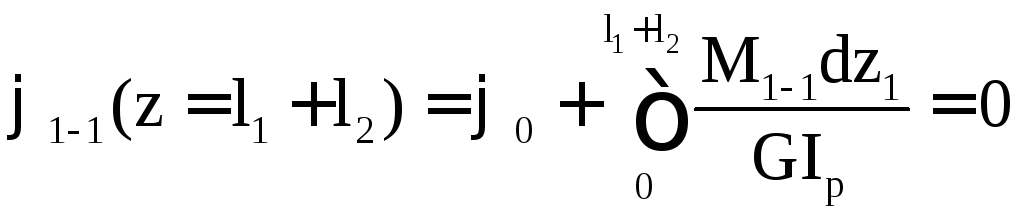
ввиду наличия заделки в точке В.

Функцией угла закручивания на участке АВ является парабола, вторая производная от которой отрицательна, следовательно, парабола выпуклая.

На участке ВС:

По полученным данным строим эпюру углов закручивания Эв долях отGI_p (рис. 2.5).

2.2.2. Расчет на жесткость.

По условию жесткости, максимальный угол поворота не должен превышать допускаемый []=0,001рад/м, то есть_max[]. Из эпюры углов поворота, построенной в долях отGI_pвидно, что максимальный угол поворота находится в сечении АПолярный момент инерции сеченияоткуда найдем диаметр стержня:

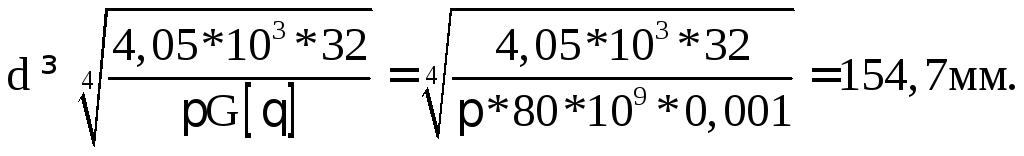
Примем (из ряда Ra40 по ГОСТ 6636-69)d=160мм.

Окончательно рассчитывая углы поворота в каждом сечении, получаем _А=-0,32*10^-3 рад/м;_В=0 рад/м;_С=0,24*10^-3рад/м;

По полученным данным строим эпюру углов закручивания Э(рис .2.5).

3. Расчет на прочность и жесткость балок и рам.

3.1. Проверочный расчет балки из прокатных профилей.

3.1.1. Расчет геометрических характеристик сечения.

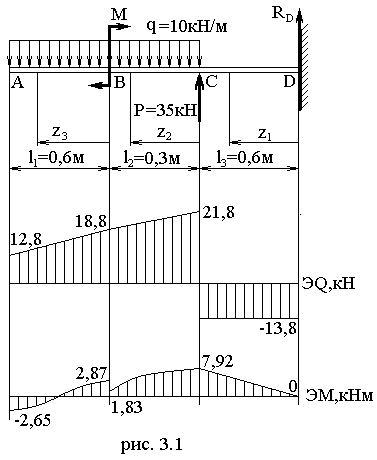
Исходные данные для расчета балки из прокатных профилей показаны на рис. 3.1. Сечение балки изображено на рис. 3.2.

Р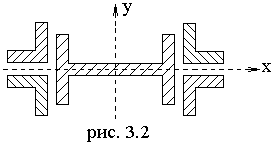ассчитаем геометрические характеристики сечения. Осевой момент инерции для двутавра профиля №20I_{x I}=115см⁴(по ГОСТ 8240-56).

Осевой момент сопротивления W_xI=W_yI=23,1см³.

Осевой момент инерции для равнобокого уголка профиля №9 I_{x L}=82,1см⁴(по ГОСТ 8240-56).

Для составного сечения:

3.1.2. Построение эпюр внутренних силовых факторов.

Найдем реакцию в заделке D(рис. 3.1):

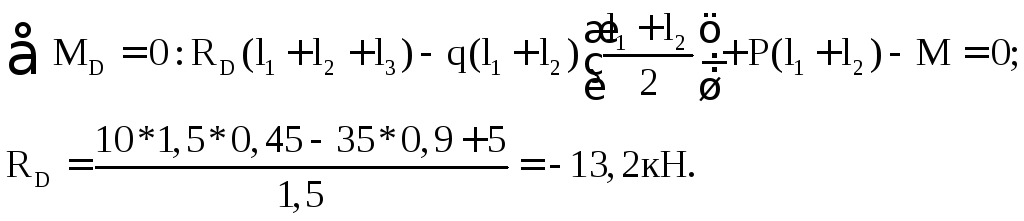
Построим эпюры перерезывающих сил и изгибающих моментов. Возьмем произвольное сечение на первом участке DC(0z₁l₃). Запишем уравнения для перерезывающей силы и изгибающего момента в произвольном сечении в пределах этого участка и рассчитаем их значения в характерных точках:

Возьмем произвольное сечение на первом участке CB(0z₂l₂). На данном участке:

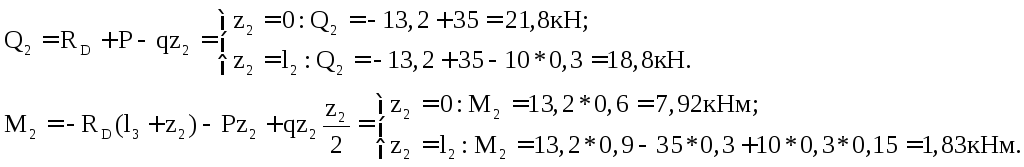
Для участка ВА (0z₃l₁), уравнения имеют вид:

3.1.3. Расчет на прочность.

Материал двутавра и уголков Ст30. Допускаемые напряжения []=282МПа. Рассчитаем максимальные напряжения, возникающие в балке, они находятся в сечении, где изгибающий момент достигает наибольшего значенияM_max=7,92кНм:

Условие прочности имеет вид _max[]. Условие прочности не выполняется_max=342,9МПа > []=282МПа. Необходимо взять профиль больших размеров. Для этого, исходя из условия прочности, определим необходимое минимальное значение осевого момента сопротивления:

Выберем двутавр – ближайший из ряда двутавр №22 W_x=28,6см³, тогдаОткуда максимальные напряжения

- условие прочности выполняется.