
- •Лекции 1 курс 1 семестр
- •1. Элементы линейной алгебры Лекция определители и системы уравнений
- •1.1. Основные определения
- •Определители n-го порядка
- •Лекция на тему «Формулы Крамера»
- •Системы линейных уравнений
- •2.1. Основные понятия
- •2.2. Методы решения систем n линейных уравнений c n переменными
- •2.2.1. Формулы Крамера
- •А) методом разложения по первому столбцу:
- •1. 2. (Нет решения);
Лекции 1 курс 1 семестр
1. Элементы линейной алгебры Лекция определители и системы уравнений
Рассмотрим основные определения, свойства и правила вычисления определителей.
1.1. Основные определения
Рассмотрим квадратную матрицу, т.е. квадратную таблицу чисел, состоящую из n строк и столбцов
 .
.
Так называемым определителем n-го порядка, соответствующим матрице А,
является следующее
выражение:
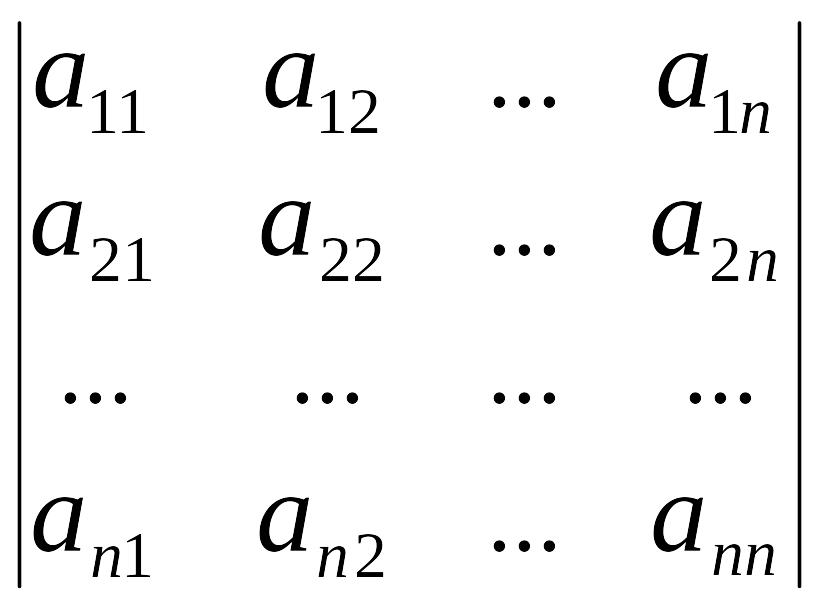 или det A или
или det A или
![]() .
.
Определители n-го порядка
Пусть дана квадратная матрица порядка n

Соединим любые 2 элемента матрицы отрезком прямой (кроме прямых вертикальных и горизонтальных, т.е. наклонной. Отрезки, которые идут слева сверху вниз направо называются положительными. Отрезки, которые идут сверху справа вниз налево называются отрицательными. Определитель (детерминант) n-го порядка соответствующий этой матрице обозначается так:
Определитель – это число. Оно равно алгебраической сумме элементов матрицы так, что каждое слагаемое содержит ровно по одному элементу из каждого столбца и ровно по одному элементу из каждой строки. Знак слагаемого определяется так: если число колонок отриц. четно, то плюс, если число нечетно, то минус.
Определитель 2-го порядка вычисляется по формуле:
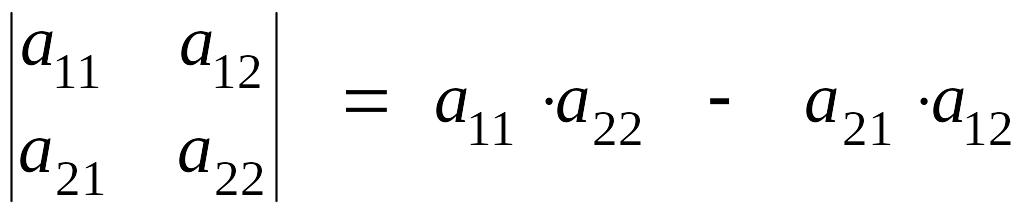 ,
,
при этом
![]() принято называть элементами главной
диагонали,
а
принято называть элементами главной
диагонали,
а
![]() - элементами побочной
диагонали данного определителя. Таким
образом, определитель 2-го порядка равен
разности произведений элементов, стоящих
на главной и побочной диагоналях.
- элементами побочной
диагонали данного определителя. Таким
образом, определитель 2-го порядка равен
разности произведений элементов, стоящих
на главной и побочной диагоналях.
Примеры.
1.
Вычислить определители: а)
![]() ;
б)
;
б)
![]() .
.
Решение. а)
=
![]() =
=
![]() ;
;
б)
=
![]() .
.
2.
Решить уравнение
![]() .
.
Решение. .
Раскроем определитель 2-го порядка, тогда в левой части уравнения получим:
![]()
![]() .
.
Тогда данное уравнение принимает вид:
![]() .
.
Ответ.
![]()
![]()
Определитель 3-го порядка вычисляется по формуле:
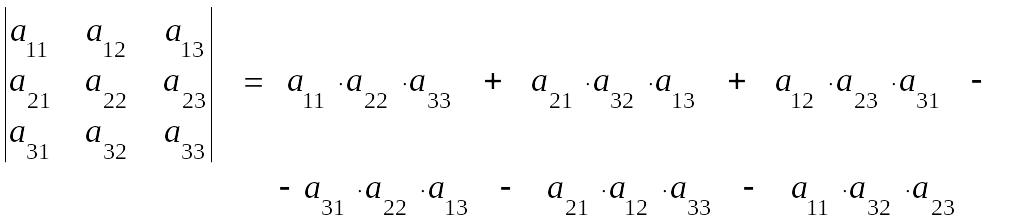
В составлении формулы помогают следующие две схемы (правило Саррюса):
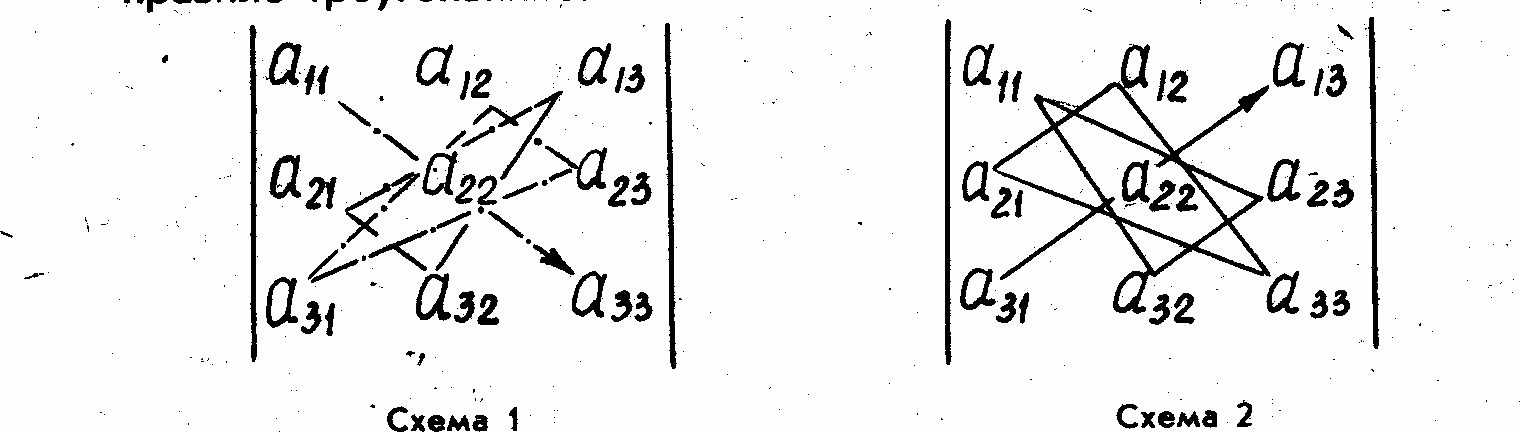
Со знаком «+» берутся произведения элементов, стоящих на главной диагонали и в вершинах двух треугольников, у которых одна из сторон параллельна главной диагонали (схема 1).
Остальные слагаемые вычисляются по схеме 2, где за основу взята побочная диагональ. При этом произведения, вычисленные по второй схеме, берутся с обратным знаком.
Пример.
Вычислить
определитель третьего порядка:
 .
.
Решение. 1.
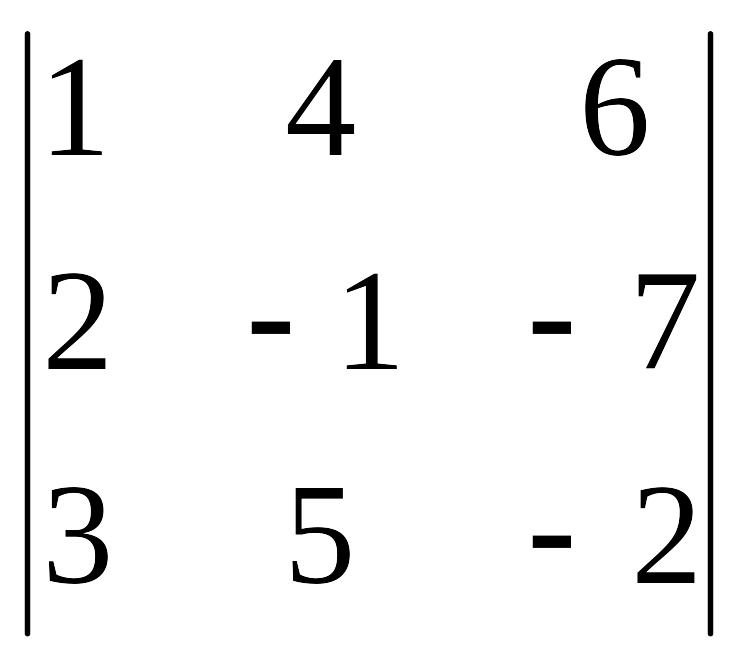
![]() .
.
Вычислили произведения, которые берутся со своим знаком.
2.
![]() .
.
Вычислили произведения, которые берутся с обратным знаком.
3.
![]()
![]() .
.
При вычислении определителя третьего порядка можно использовать другое правило.
К матрице, для которой составлен определитель третьего порядка, допишем справа еще раз первый, а затем второй столбцы:
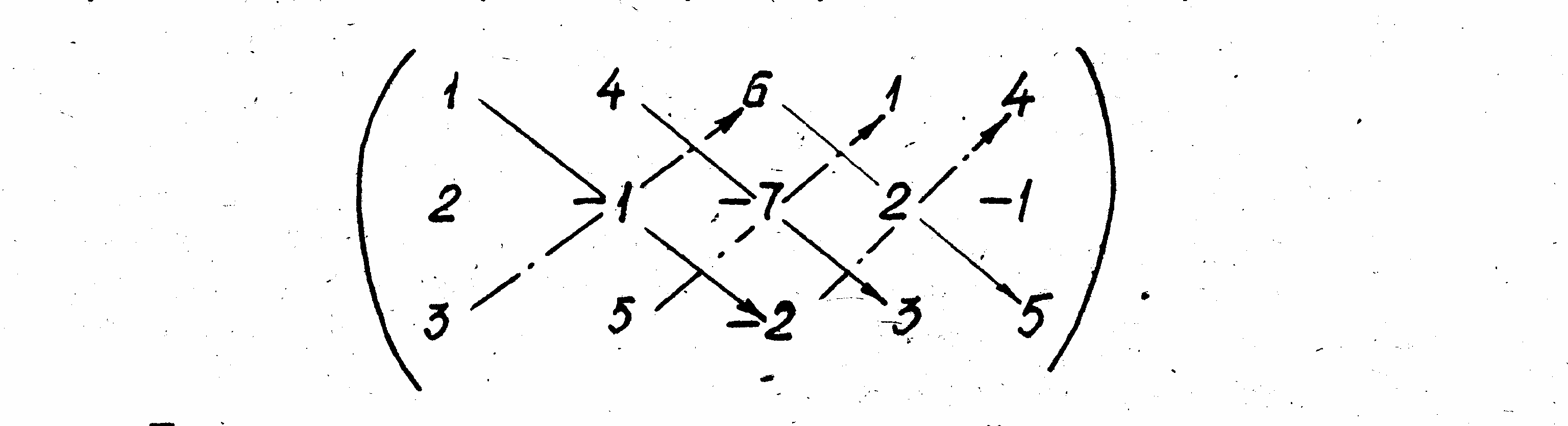
Произведения чисел, стоящих на главной диагонали и на диагоналях, ей параллельных, берутся со своим знаком, а произведения чисел, стоящих на побочной диагонали и на диагоналях, ей параллельных, с противоположным знаком. Тогда,
![]()
Определение 1.1.1.
Рассмотрим определитель n-го порядка: = .
Выберем любой
элемент определителя
,
например,
![]() .
Вычеркнем строку и столбец, на
пересечении которых находится
,
из оставшихся элементов составим
определитель (n - 1)-го порядка. Этот
определитель называется минором
для элемента
и обозначается
.
Вычеркнем строку и столбец, на
пересечении которых находится
,
из оставшихся элементов составим
определитель (n - 1)-го порядка. Этот
определитель называется минором
для элемента
и обозначается
![]() .
.
Примеры.
Пусть дан определитель
3-го порядка:
=
 .
.
Для элемента
![]() минором является
минором является
![]() =
=
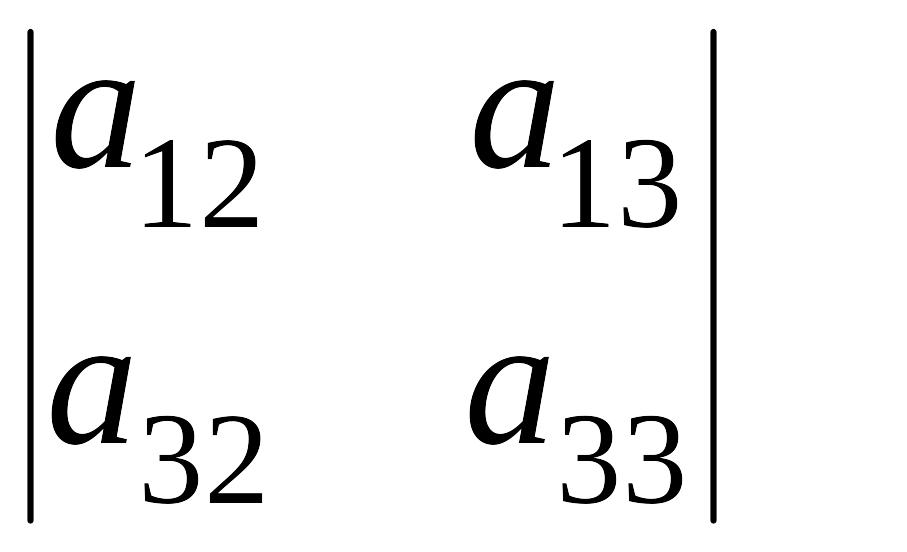 ,
,
для элемента
![]() минором является
минором является
![]() =
=
 ,
,
для элемента
![]() минором является
минором является
![]() =
=
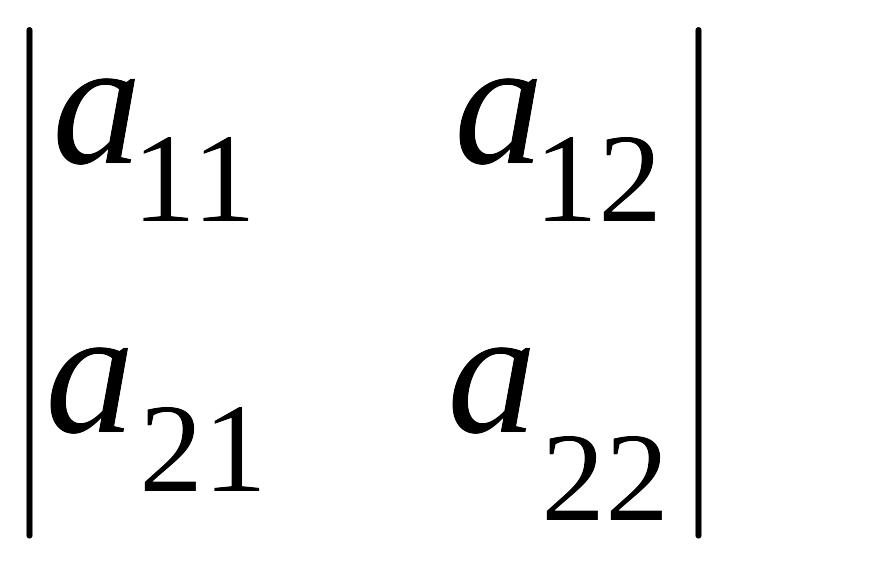 .
.
Определение 1.1.2.
Алгебраическим
дополнением
элемента
определителя n-го порядка (обозначается
А![]() )
называется его минор, взятый со знаком
(—1)
)
называется его минор, взятый со знаком
(—1)![]() ,
где i — номер строки, j — номер столбца,
на пересечении которых находится элемент
,
т.е.
,
где i — номер строки, j — номер столбца,
на пересечении которых находится элемент
,
т.е.
![]() .
.
1.2. Свойства определителей.
1.2.1. Определитель n-го порядка равен сумме произведений элементов какой-либо строки (столбца) на соответствующие им алгебраические дополнения
(это свойство позволяет свести вычисление определителя n-го порядка к определителю (n—1)-го порядка и носит название - «разложение определителя по элементам какой-либо строки (столбца)»):
![]()
(приведены разложения
по элементам 1-ой строки, 3-го столбца
соответственно и т.д.). В общем случае
![]() .
.
Поясним это свойство на примере определителя третьего порядка:
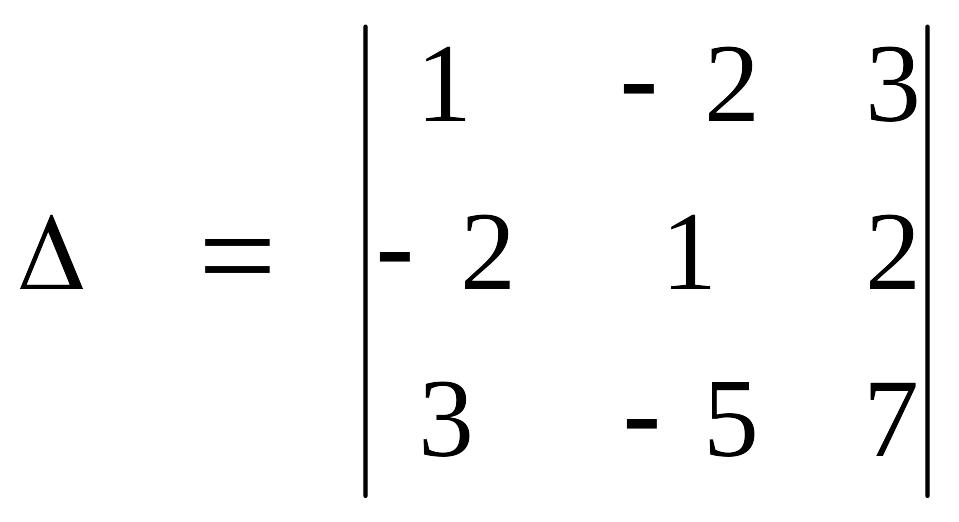 .
.
Разложим определитель по элементам 1-ой строки:
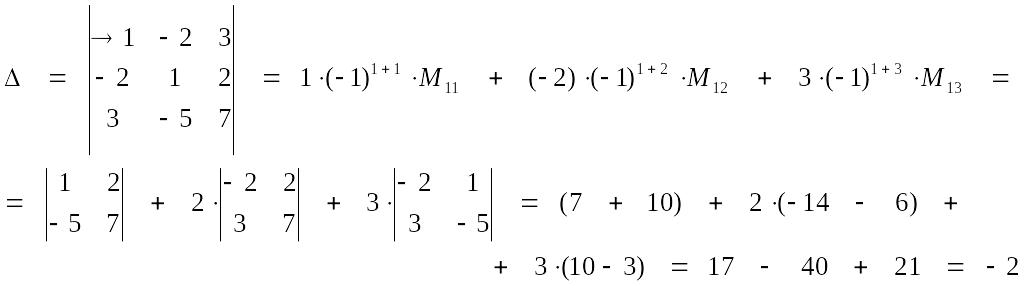
Разложим определитель по элементам 2-го столбца:
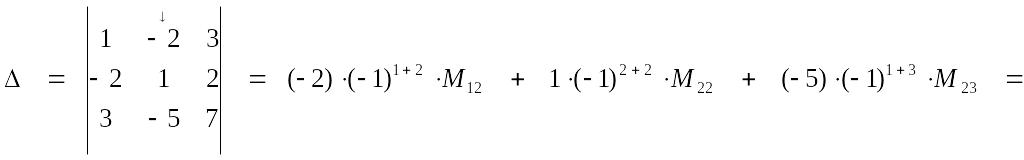
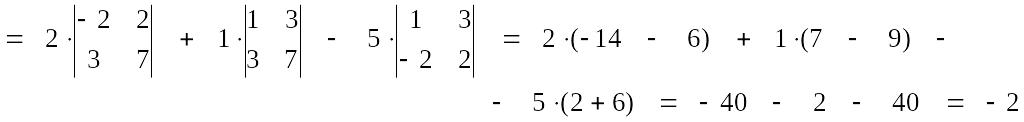
1.2.2. При замене всех строк определителя на столбцы с теми же номерами величина его не изменится (равноправность строк и столбцов), т. е.
=
 .
.
1.2.3. При перестановке местами двух строк (столбцов) определитель меняет свой знак на противоположный, т.е. например,
=
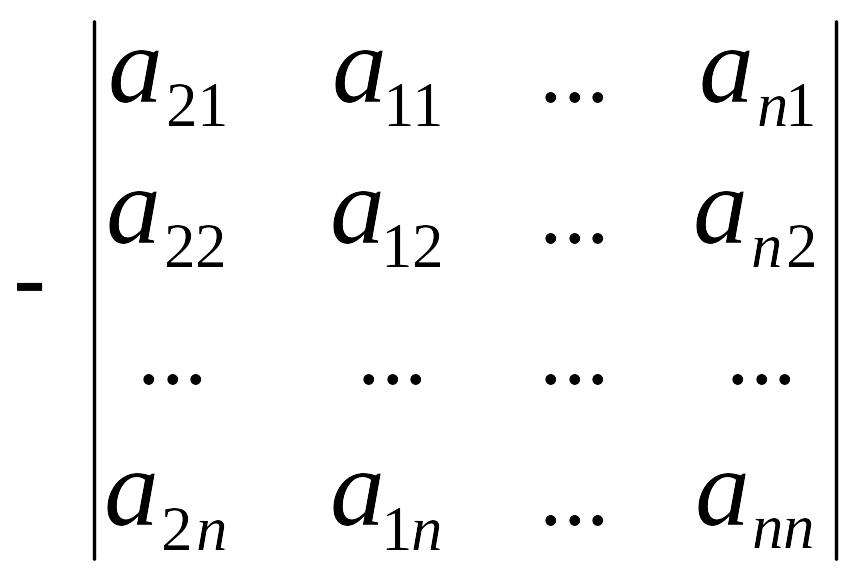
(поменялись местами 1-й и 2-ой столбцы).
1.2.4.
Умножение всех элементов какой-либо
строки (столбца) определителя на одно
и то же число
![]() равносильно умножению на
определителя.
равносильно умножению на
определителя.
Иными словами, общий множитель всех элементов данной строки (столбца) можно вынести за знак определителя, т.е. например,
1)
 =
=
![]() ;
;
2)

1.2.5. Если элементы некоторой строки (столбца) нули, то определитель равен нулю.
1.2.6. Если элементы какой-либо строки (столбца) определителя пропорциональны (в частности, равны) соответствующим элементам другой строки (столбца), то определитель равен нулю, т.е. например,
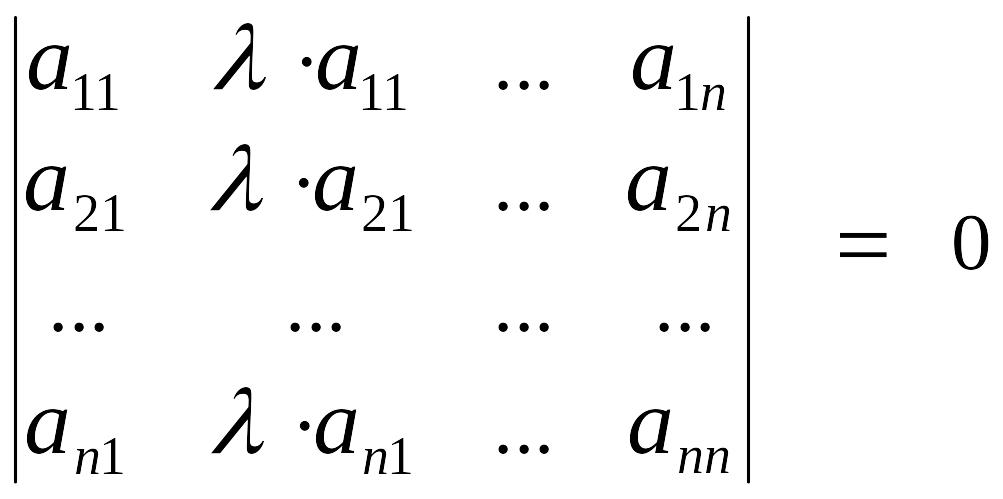 (
элементы 1и 2 столбцов определителя
пропорциональны)
(
элементы 1и 2 столбцов определителя
пропорциональны)
1.2.7. Если каждый элемент k -ой строки (столбца) (k =1, 2, ..., n) определителя представляет собой сумму двух слагаемых, то определитель равен сумме двух определителей, в одном из которых в k-ой строке (столбце) стоят первые слагаемые, а в другом — вторые; элементы, стоящие на остальных местах, у всех трех определителей одни и те же, т. е. например,

1.2.8. Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, т.е. например,
=
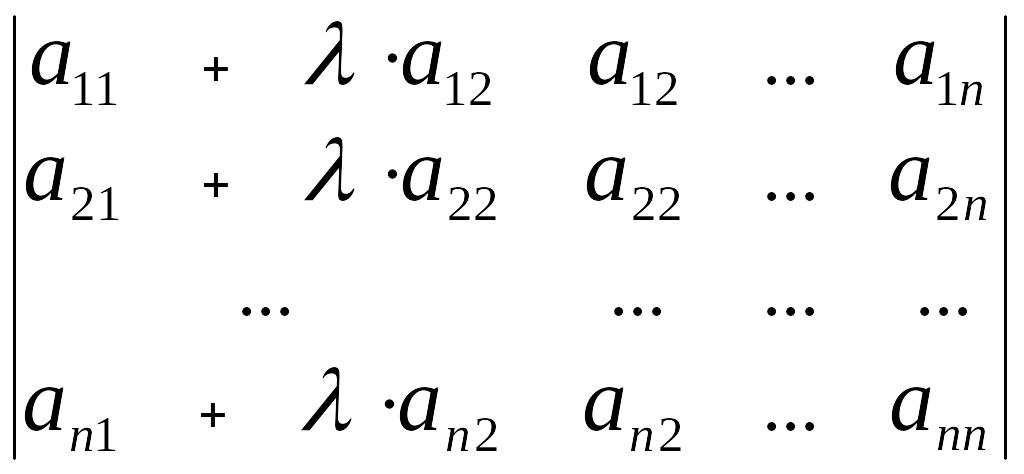
1.2.9. Если в определителе порядка n имеется столбец (строка), все элементы которого равны нулю, кроме одного, то, разложив определитель по этому столбцу (строке), сведем вычисление определителя n-го порядка к вычислению единственного определителя порядка (n - 1).
1.2.10. Если же в определителе n-го порядка нет столбца (строки), все элементы которого равны нулю, кроме одного, то, используя свойство 1.2.8. определителей, можно, не изменяя величины определителя, преобразовать его так, чтобы в выбранном столбце (строке) все элементы, кроме одного, обратились в нуль.
Пример.
Вычислить определитель
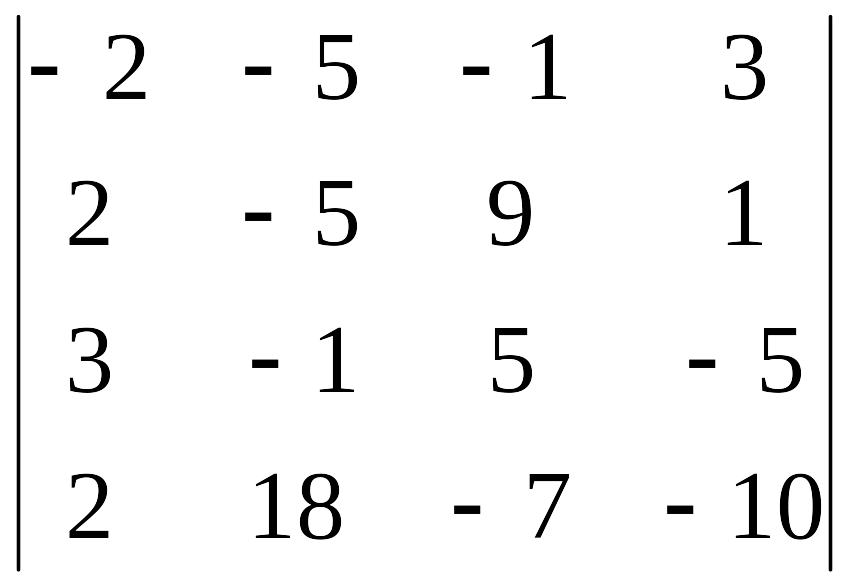 .
.
Решение. К 3-й строке прибавим 1-ю (т.е. к элементам 3-й строки прибавим соответствующие элементы 1-й строки):
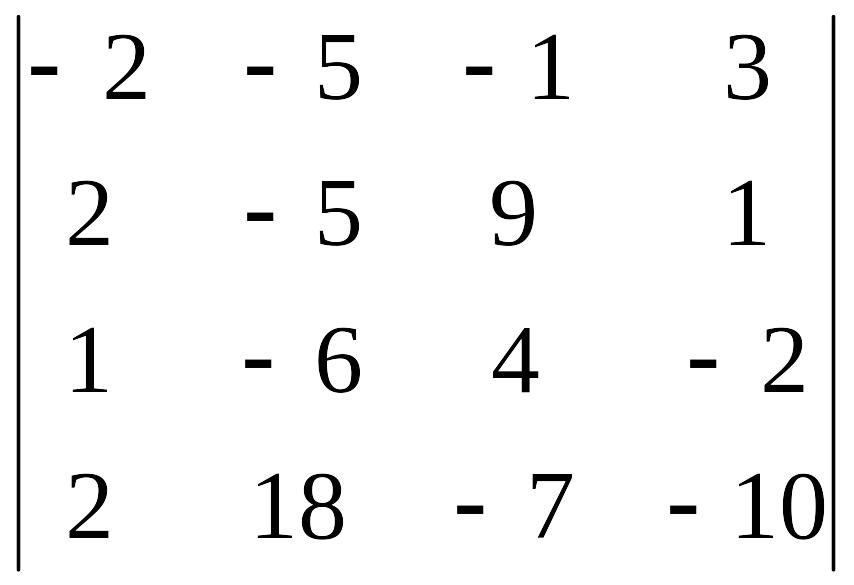
Прибавляя к первой строке удвоенную третью, ко второй – третью, умноженную на (-2), а к четвёртой строке – третью, умноженную на (-2), получим

Вынесем за знак определителя общий множитель 3-й строки и получим:

Прибавляя ко 2-й строке - 1-ую, умноженную на 5, к 3-й строке – 1-ую, умноженную на (-2), получим:
 .
.
1.2.11.
![]() .
.
1.2.12.
![]() .
.
Примеры для самостоятельного решения
1.3.1. Вычислить (раскрыть) определители:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
 ;
г)
;
г)
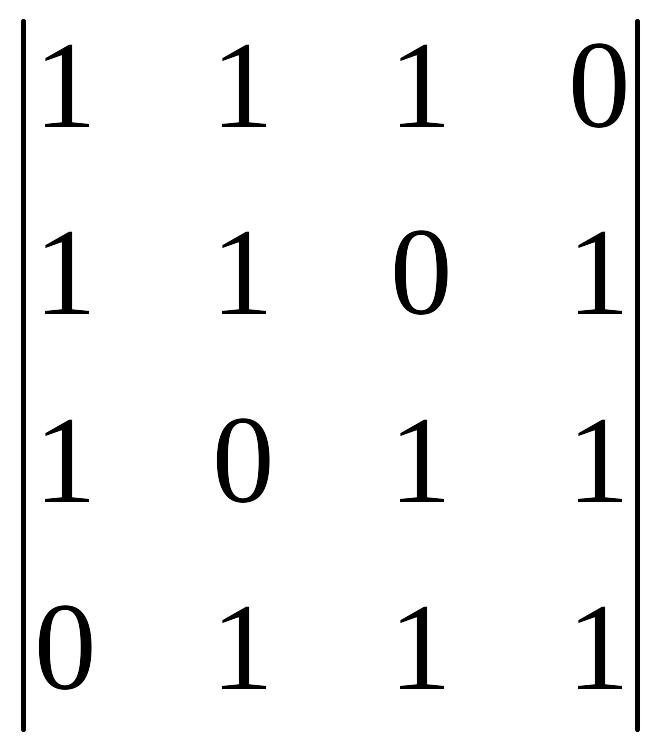 ; д)
; д)
 .
.
