Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тюменский Государственный Нефтегазовый Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Гнатюк. Линйная алгебра. РУП (ЭПО, МЭ, НН).doc

Скачиваний:

Добавлен:

18.11.2019

Размер:

3.3 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Выбор варианта

Номер варианта выбирается студентом-заочником по последней цифре номера зачетной книжки.

Задания для контрольных работ

Задача 1-10. На плоскости заданы вершины треугольника . Найти 1) уравнение прямой ; 2) уравнение медианы ; 3) уравнение высоты и ее длину; 4) точку пересечения высоты и стороны ; 5) длину высоты (двумя способами). Сделать чертеж.

1.	,	,	.
2.	,	,	.
3.	,	,	.
4.	,	,	.
5.	,	,	.
6.	,	,	.
7.	,	,	.
8.	,	,	.
9.	,	,	.
10.	,	,	.

Задача 11-20. Определить тип кривой, привести уравнение к каноническому виду. Кривую построить.

11.	а)	,	б)	,
	в)	,	г)	.
12.	а)	,	б)	,
	в)	,	г)	.
13.	а)	,	б)	,
	в)	,	г)	.
14.	а)	,	б)	,
	в)	,	г)	.
15.	а)	,	б)	,
	в)	,	г)	.
16.	а)	,	б)	,
	в)	,	г)	.
17.	а)	,	б)	,
	в)	,	г)	.
18.	а)	,	б)	,
	в)	,	г)	.
19.	а)	,	б)	,
	в)	,	г)	.
20.	а)	,	б)	,
	в)	,	г)	.

Задача 21-30. Построить по точкам график функции в полярной системе координат. Значения функции вычислять в точках , .

21.	.	22.	.
23.	.	24.	.
25.	.	26.	.
27.	.	28.	.
29.	.	30.	.

Задача 31-40. Коллинеарны ли векторы и , построенные по векторам и ?

31.	,	,	,	.
32.	,	,	,	.
33.	,	,	,	.
34.	,	,	,	.
35.	,	,	,	.
36.	,	,	,	.
37.	,	,	,	.
38.	,	,	,	.
39.	,	,	,	.
40.	,	,	,	.

Задача 41-50. Компланарны ли векторы , и ?

41.	,	,	.
42.	,	,	.
43.	,	,	.
44.	,	,	.
45.	,	,	.
46.	,	,	.
47.	,	,	.
48.	,	,	.
49.	,	,	.
50.	,	,	.

Задача 51-60. Найти расстояние от точки до плоскости, проходящей через точки , , .

51.	,	,	,	.
52.	,	,	,	.
53.	,	,	,	.
54.	,	,	,	.
55.	,	,	,	.
56.	,	,	,	.
57.	,	,	,	.
58.	,	,	,	.
59.	,	,	,	.
60.	,	,	,	.

Задача 61-70. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору .

61.	,	,	.
62.	,	,	.
63.	,	,	.
64.	,	,	.
65.	,	,	.
66.	,	,	.
67.	,	,	.
68.	,	,	.
69.	,	,	.
70.	,	,	.

Задача 71-80. Найти угол между плоскостями.

71.	, .	72.	, .
73.	, .	74.	, .
75.	, .	76.	, .
77.	, .	78.	, .
79.	, .	80.	, .

Задача 81-90. Найти точку пересечения прямой и плоскости.

81.	, .	82.	, .
83.	, .	84.	, .
85.	, .	86.	, .
87.	, .	88.	, .
89.	, .	90.	, .

Задача 91-100. Найти определитель и обратную матрицу для данной матрицы . Используя полученные результаты или другим способом, решить систему уравнений .

91.	а)	, ;	б)	, .
92.	а)	, ;	б)	, .
93.	а)	, ;	б)	, .
94.	а)	, ;	б)	, .
95.	а)	, ;	б)	, .
96.	а)	, ;	б)	, .
97.	а)	, ;	б)	, .
98.	а)	, ;	б)	, .
99.	а)	, ;	б)	, .
100.	а)	, ;	б)	, .

Задача 101-110. Решить систему по формулам Крамера и матричным методом.

101.	.	102.	.
103.	.	104.	.
105.	.	106.	.
107.	.	108.	.
109.	.	110.	.

Задача 111-120. Найти общее решение в векторной форме системы линейных уравнений. Выполнить проверку.

111.		112.
113.		114.
115.		116.
117.		118.
119.		120.

Задача 121-130. Дана система векторов , , , . Убедиться, что векторы , , линейно независимы и образуют базис системы векторов , , , . Вектор , не вошедший в базис, разложить по базису. Выполнить проверку.

121.	,	,	,	.
122.	,	,	,	.
123.	,	,	,	.
124.	,	,	,	.
125.	,	,	,	.
126.	,	,	,	.
127.	,	,	,	.
128.	,	,	,	.
129.	,	,	,	.
130.	,	,	,	.

Задача 131-140. Даны два линейных преобразования и . Средствами матричного исчисления найти преобразование, выражающее через .

131.
132.
133.
134.
135.
136.
137.
138.
139.
140.

Задача 141-150. Найти матрицу , которая приводит матрицу к диагональному виду. Выполнить проверку .

141.	.	142.	.
143.	.	144.	.
145.	.	146.	.
147.	.	148.	.
149.	.	150.	.

Задача 151-160. С помощью ортогональной матрицы привести данную симметрическую матрицу к диагональному виду. Выполнить проверку .

151.	.	152.	.
153.	.	154.	.
155.	.	156.	.
157.	.	158.	.
159.	.	160.	.

Задача 161-170. Найти линейное преобразование неизвестных , , , приводящее квадратичную форму к каноническому виду. Результат проверить. Выяснить, является ли квадратичная форма знакоопределенной.

161.	.
162.	.
163.	.
164.	.
165.	.
166.	.
167.	.
168.	.
169.	.
170.	.

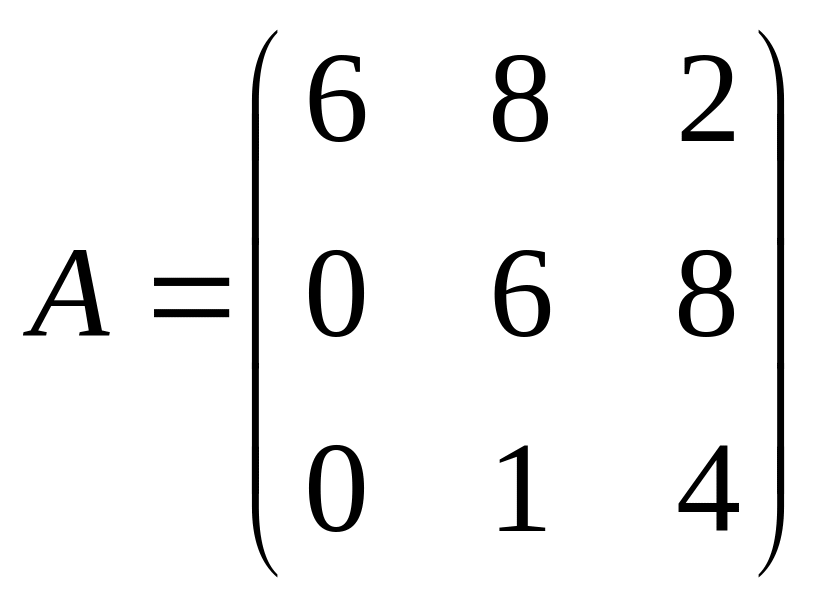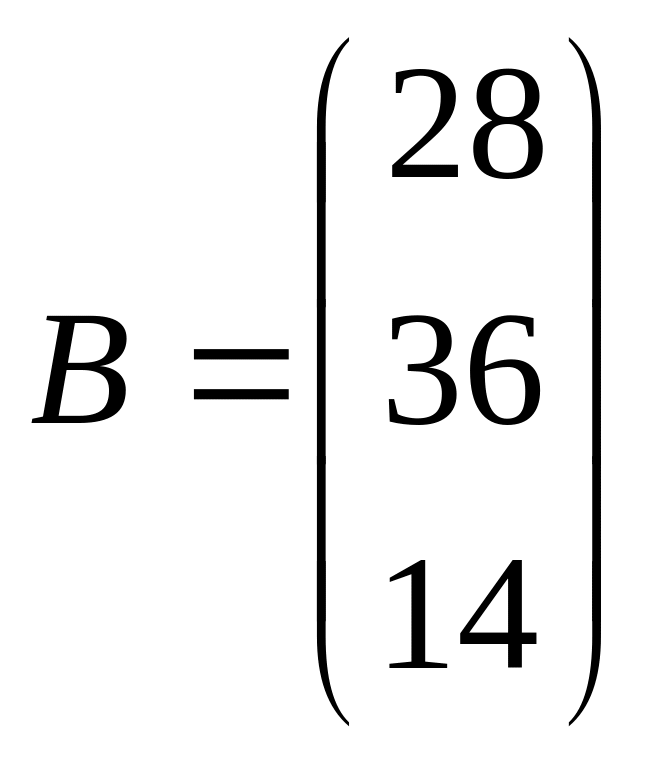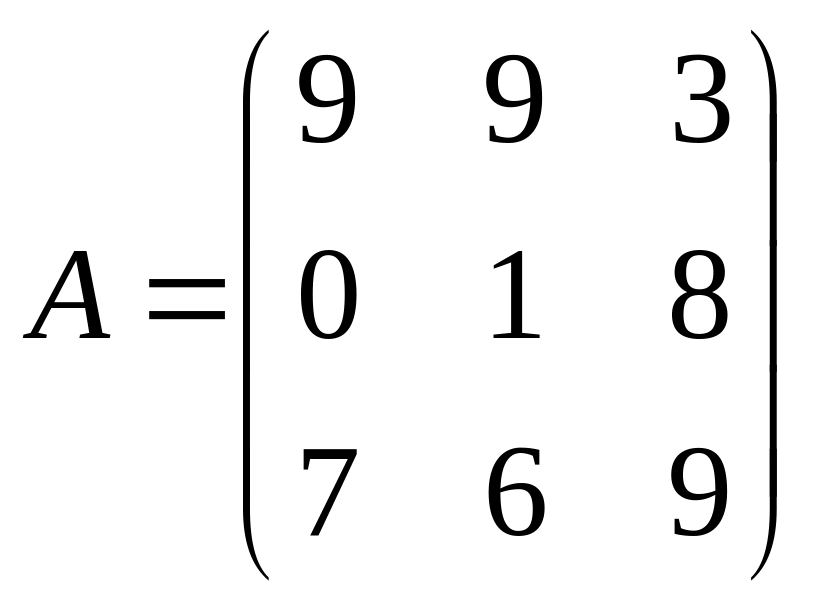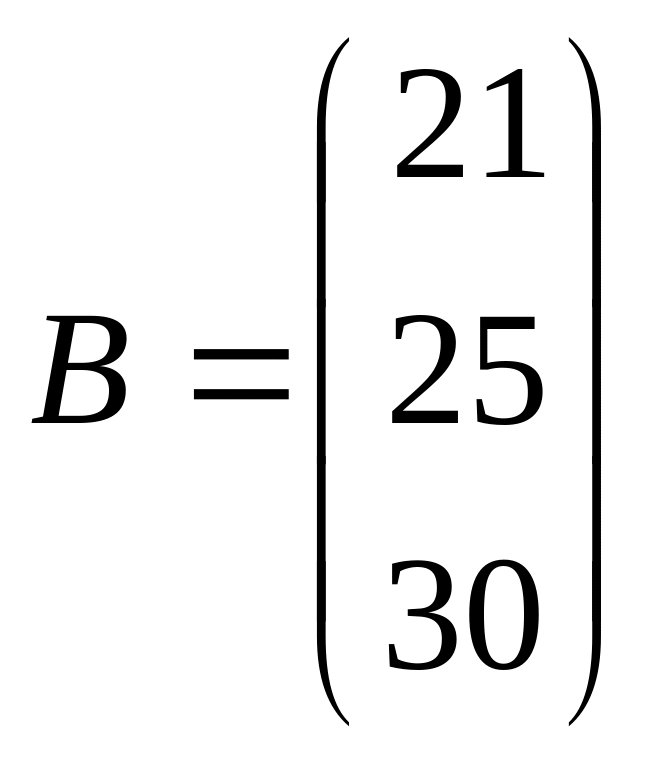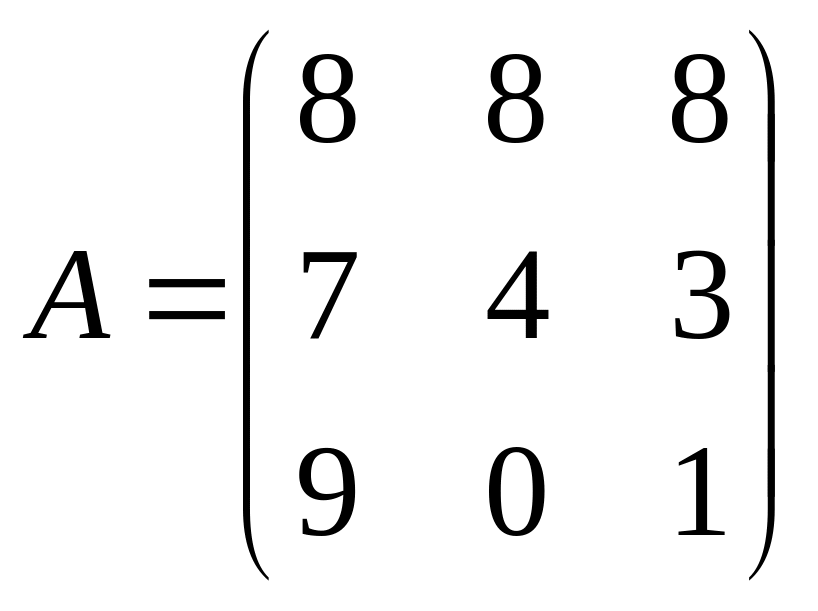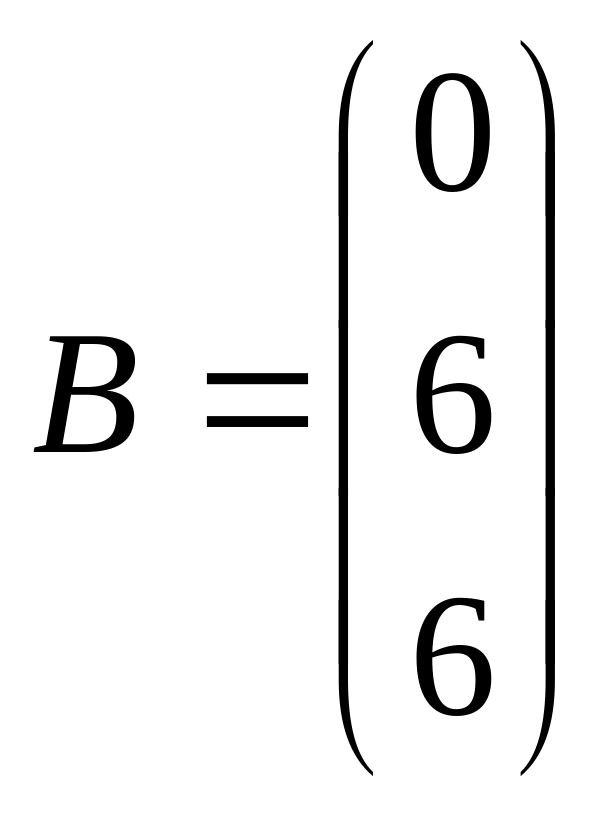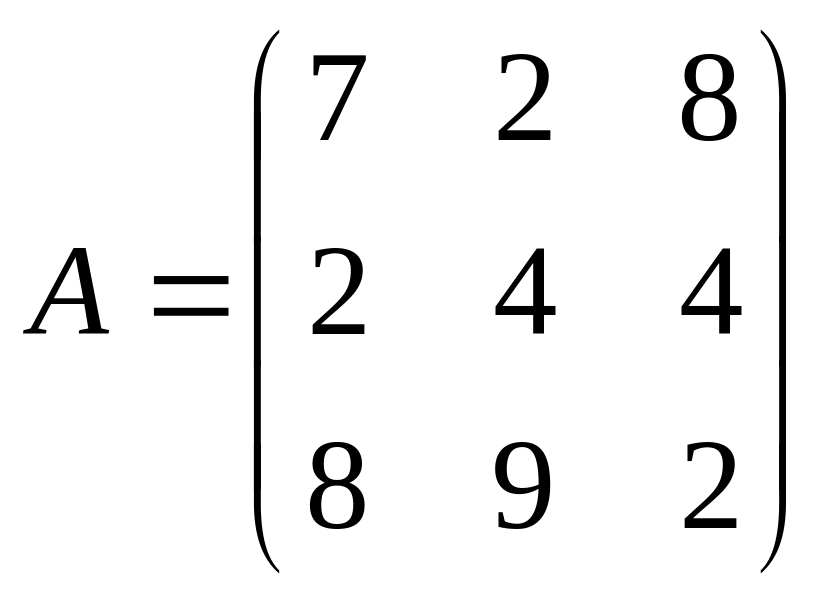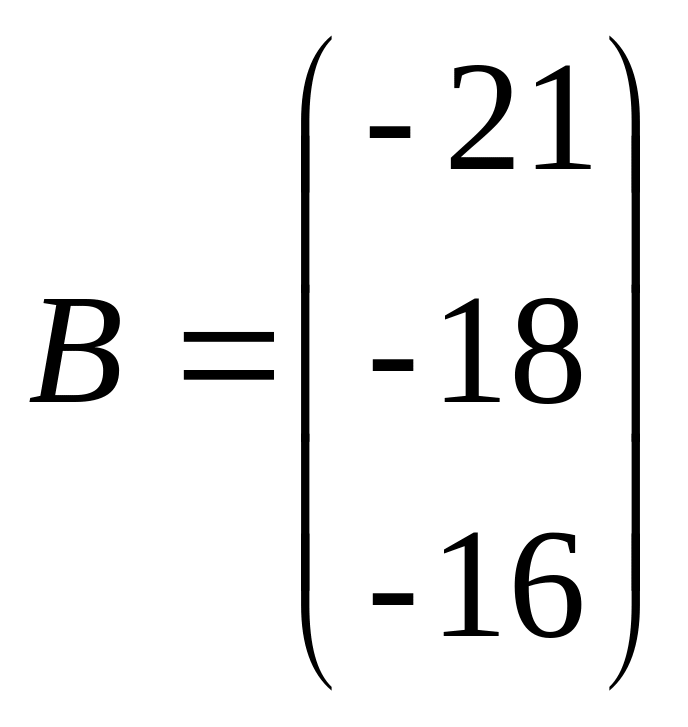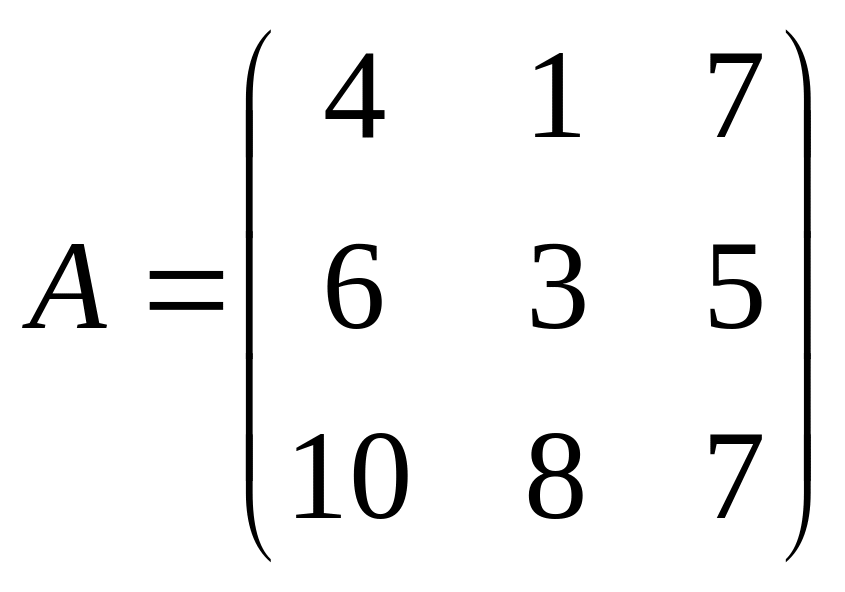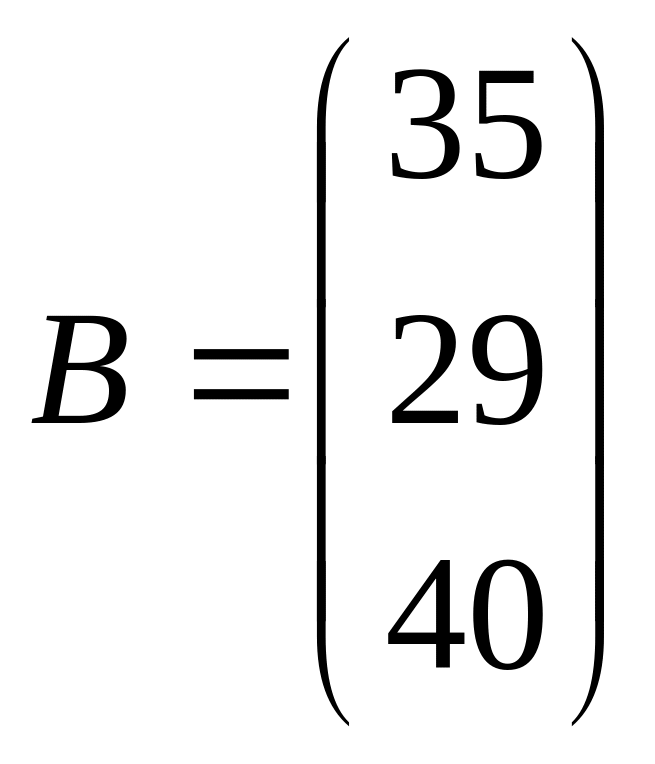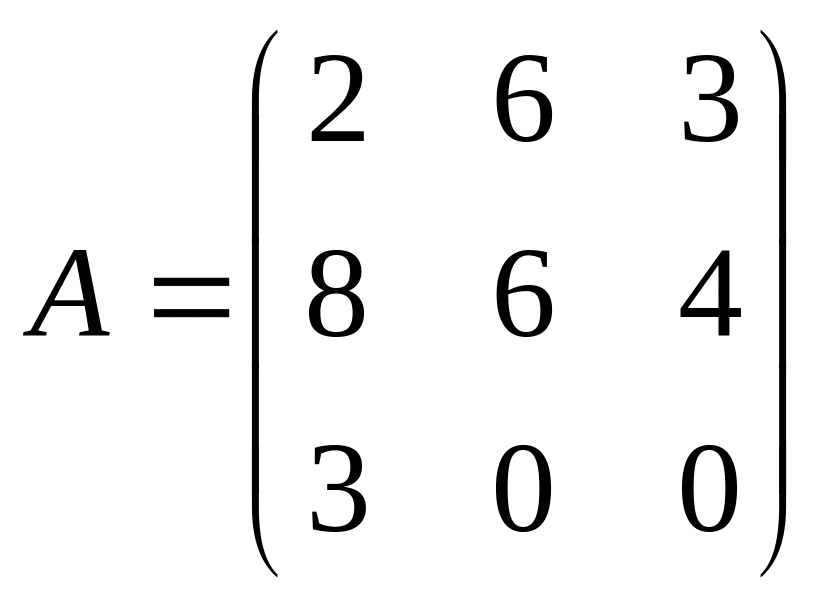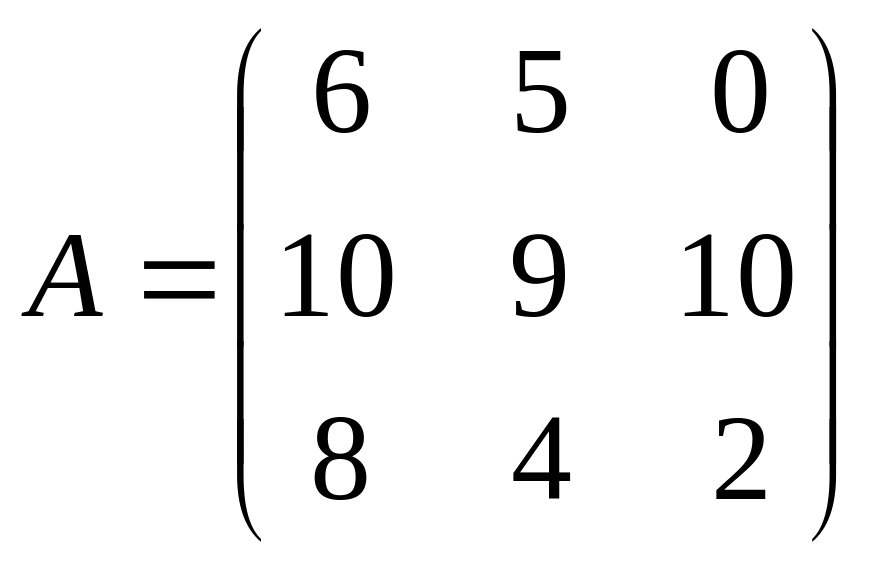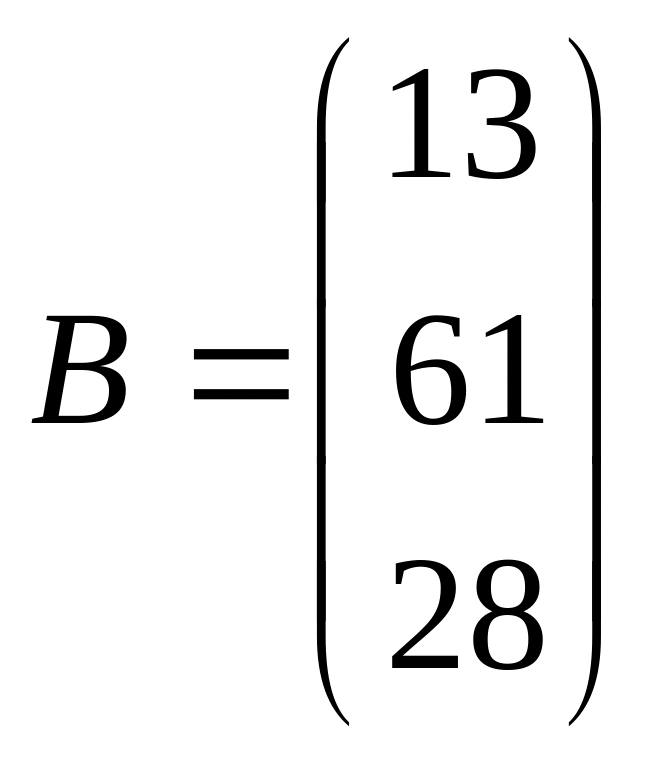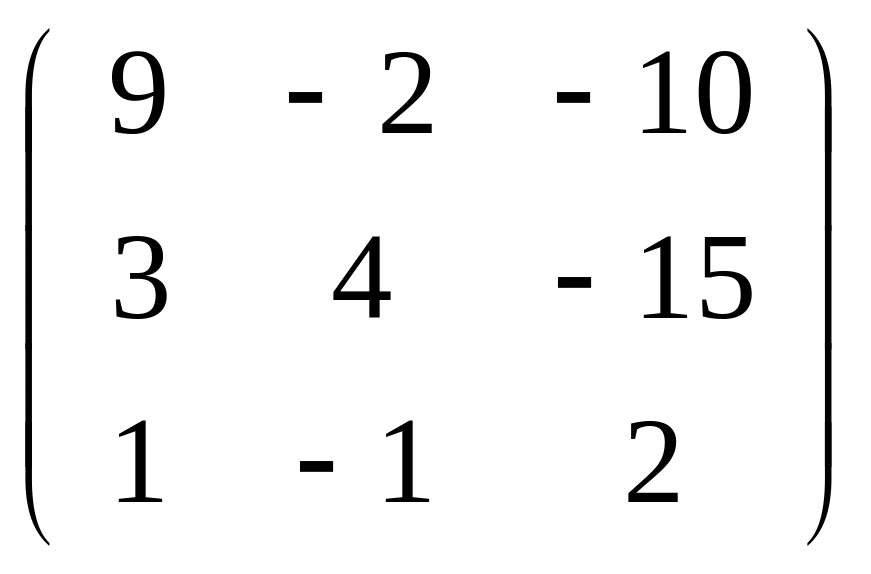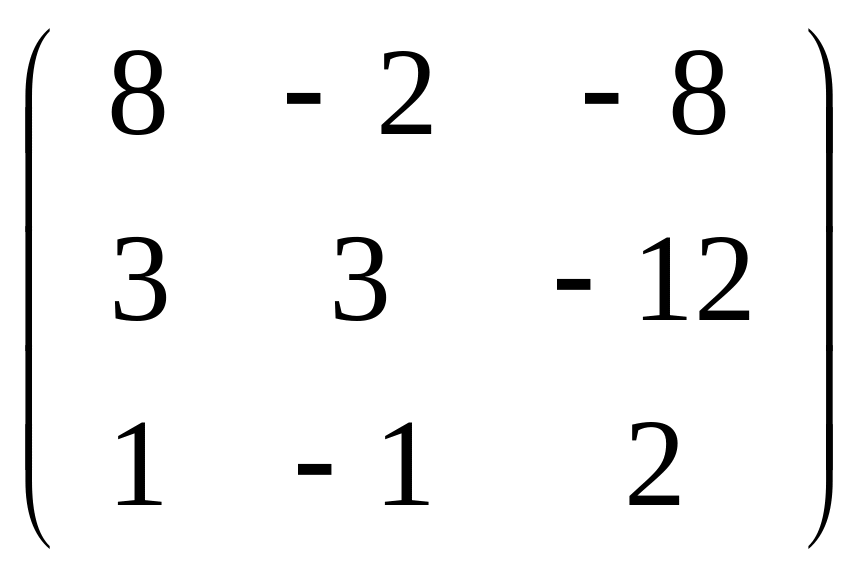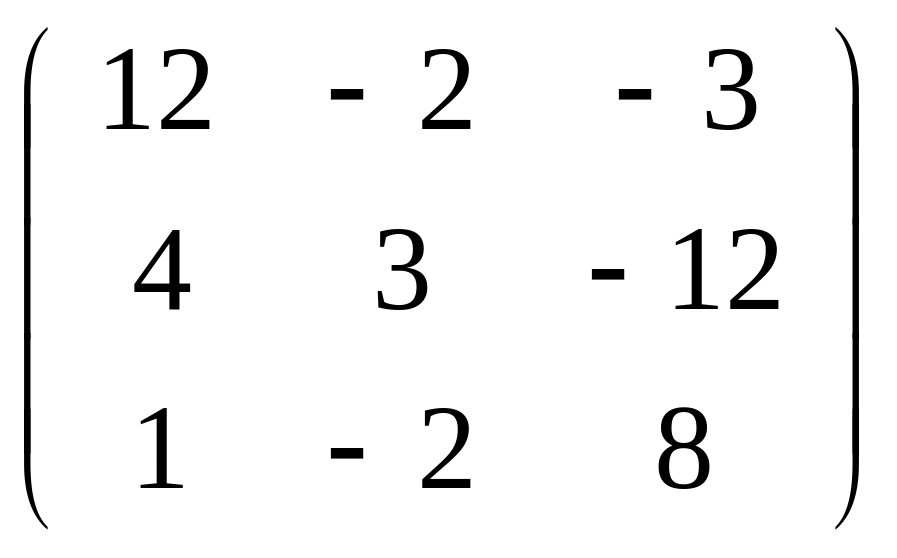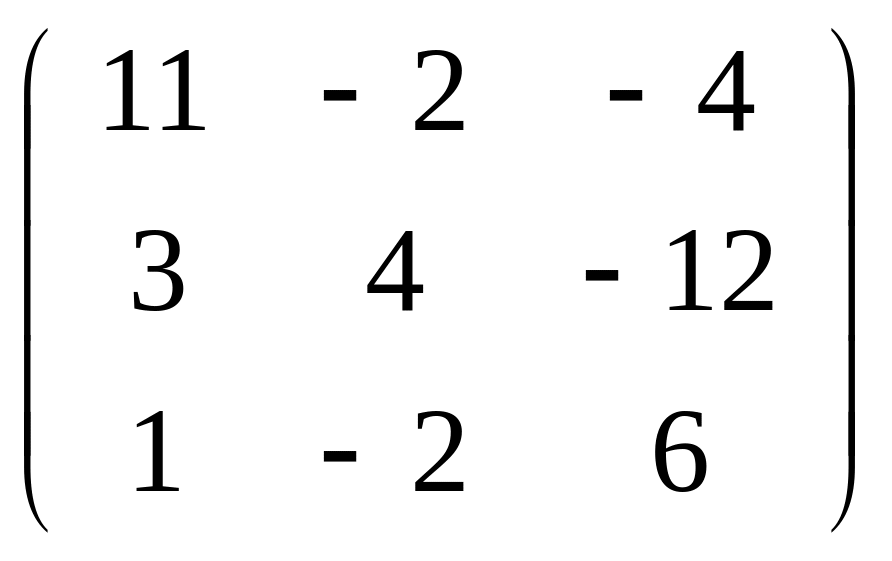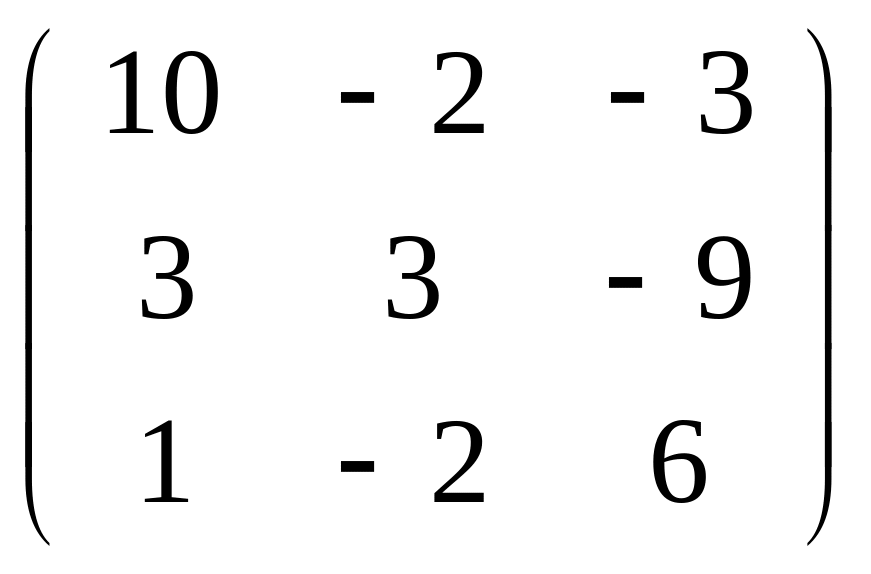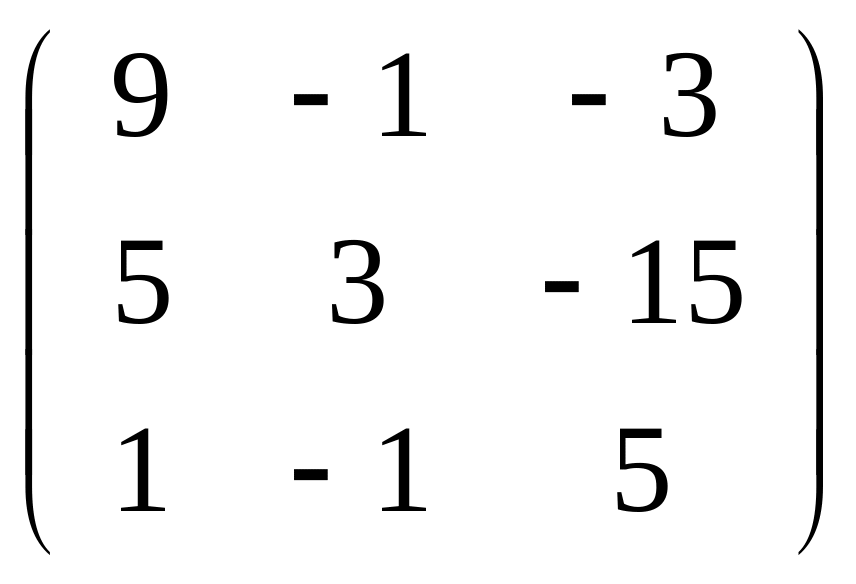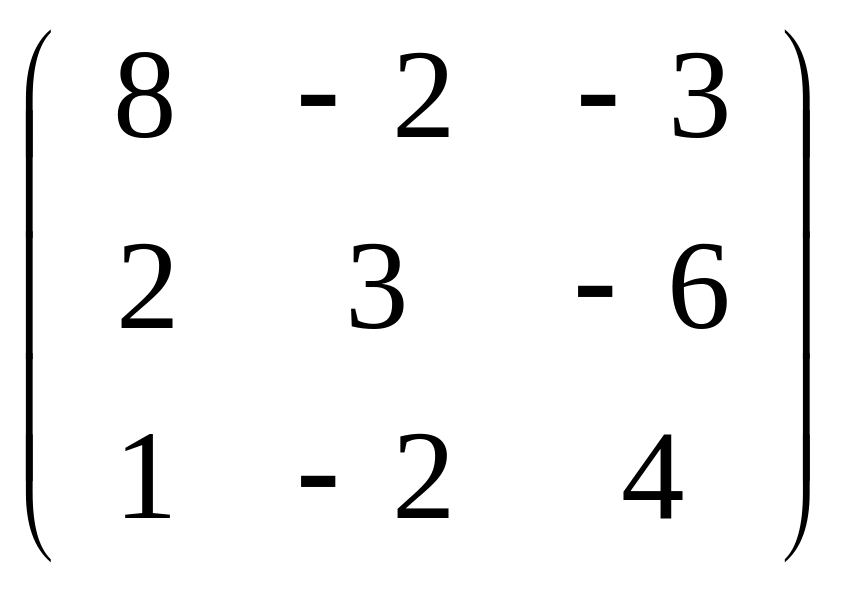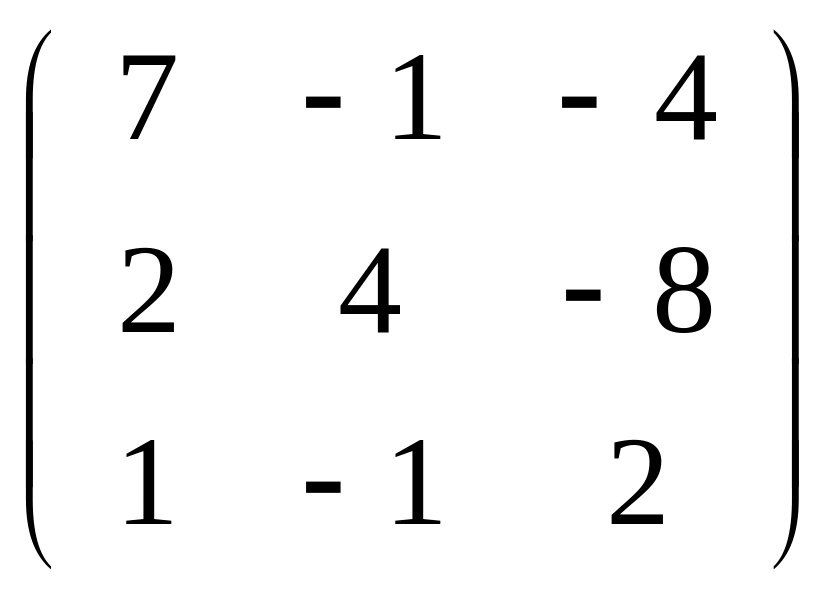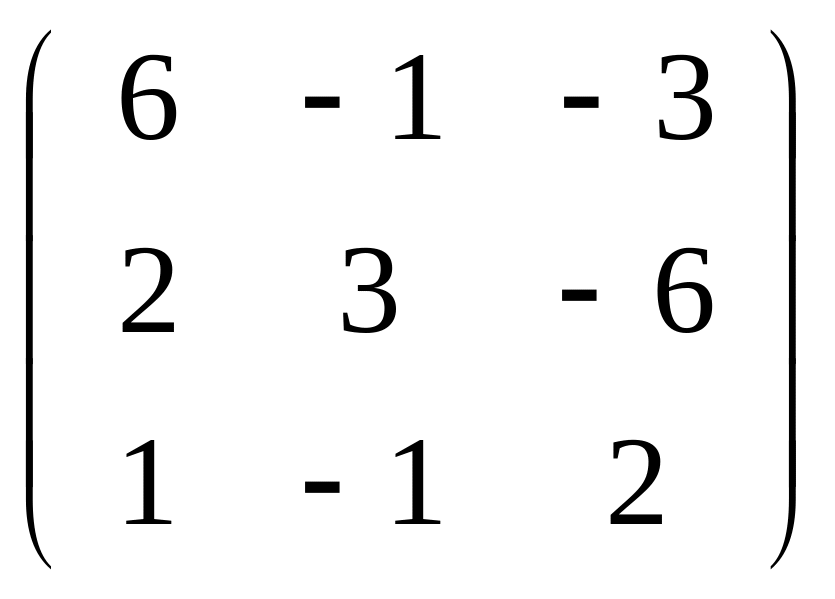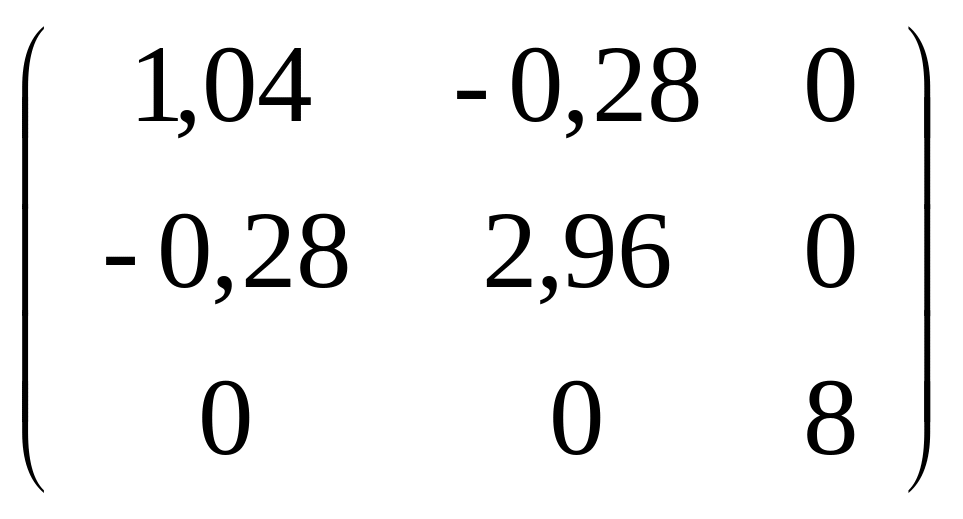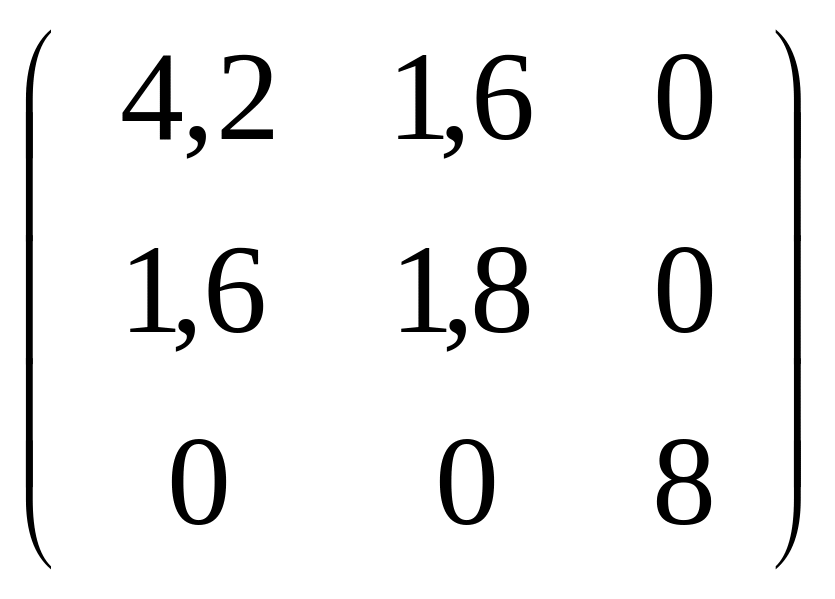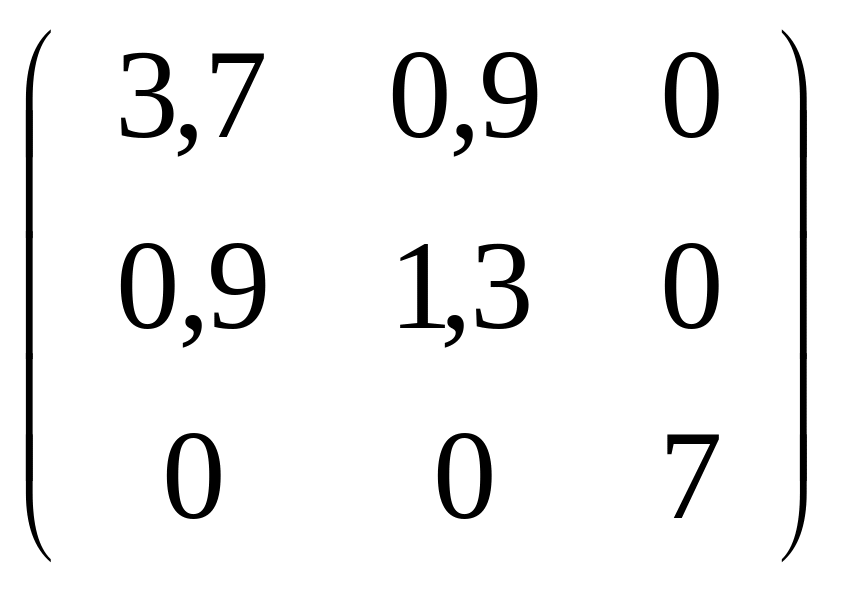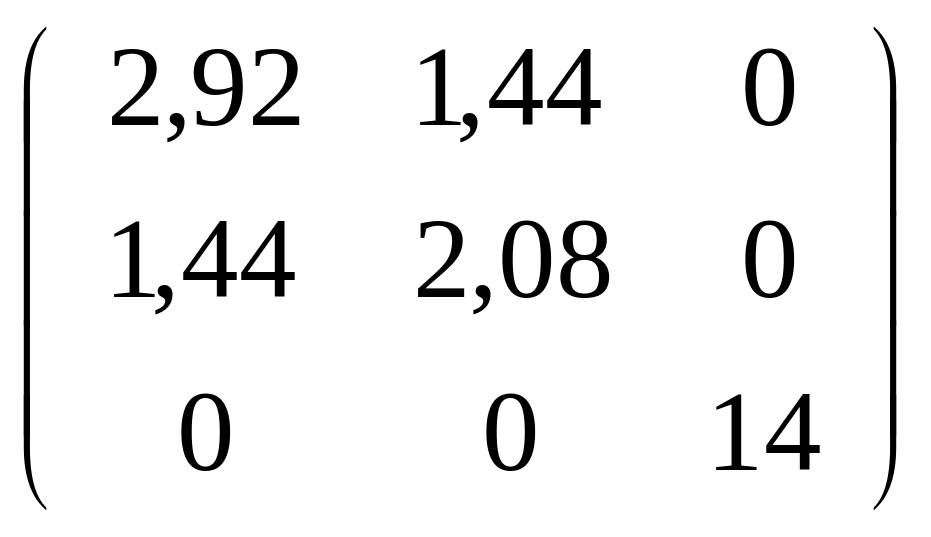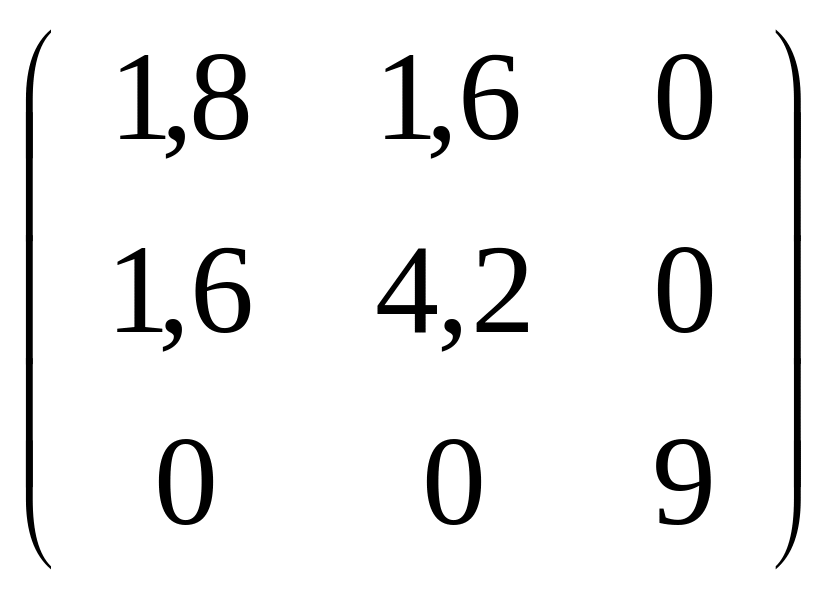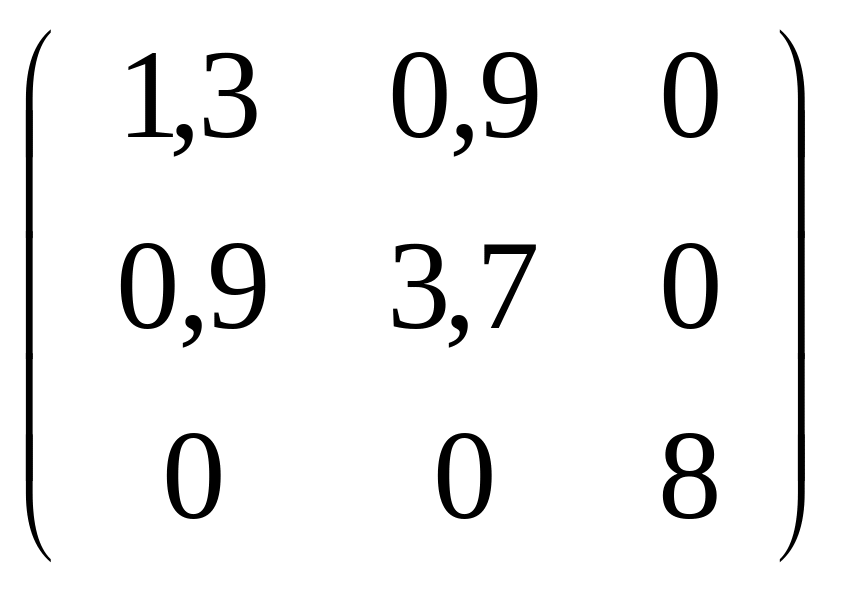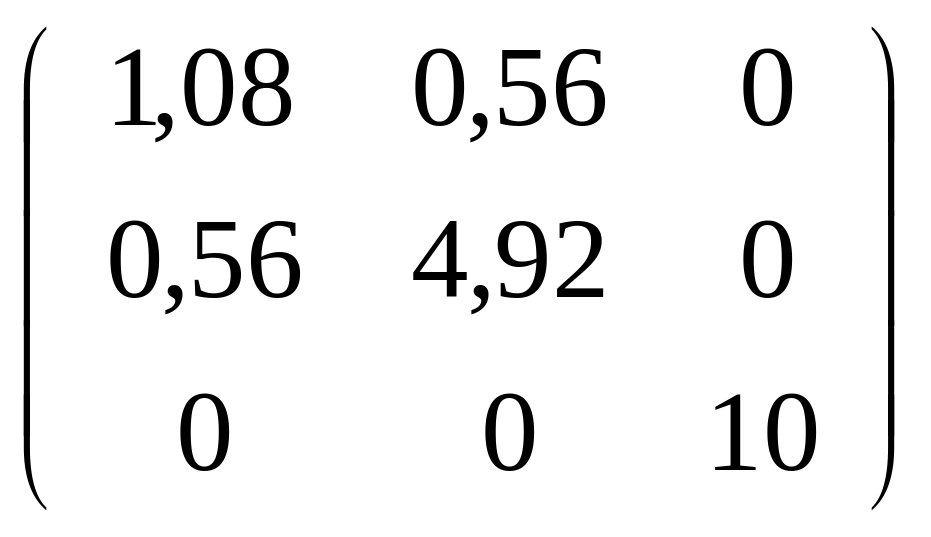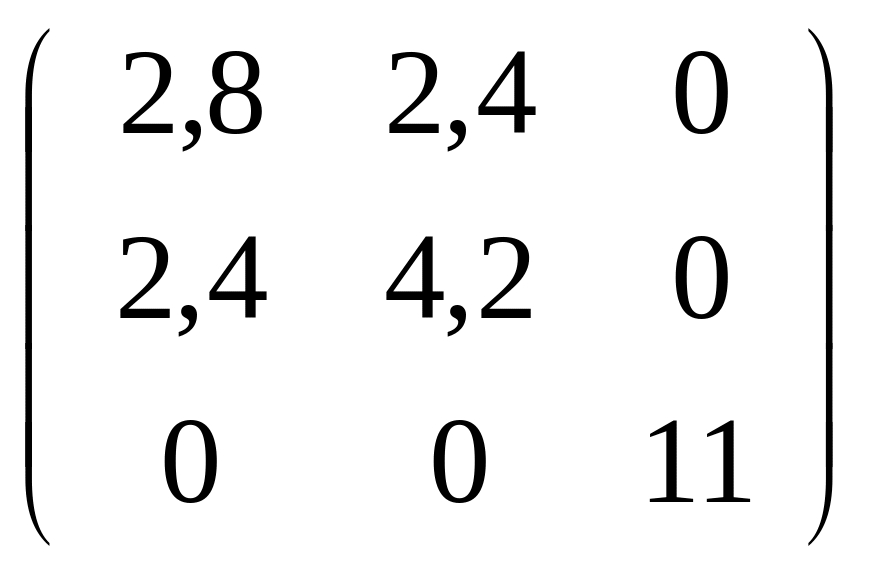<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.11.2019290.82 Кб38Глава 9.DOC
#
20.12.201836.68 Кб23Глазунов 1-2 атт.docx
#
17.02.201677.31 Кб4ГМУ-4 курс.doc
#
28.10.201882.94 Кб2ГМУ-учебно-ознакомит.практика.doc
#
15.09.201976.29 Кб3ГМУ__11.doc
#
18.11.20193.3 Mб6Гнатюк. Линйная алгебра. РУП (ЭПО, МЭ, НН).doc
#
14.11.201923.17 Кб2горбунов%20роман,%20реферат[1].docx
#
15.07.2019765.95 Кб6Гордеев Н.В. Русский оборонительный доспех.doc
#
22.09.201923.66 Кб4ГОС 3.docx
#
17.02.2016787.85 Кб220гос.docx
#
22.09.201928.35 Кб6ГОСС.docx

11.	а)	,	б)	,
	в)	,	г)	.
12.	а)	,	б)	,
	в)	,	г)	.
13.	а)	,	б)	,
	в)	,	г)	.
14.	а)	,	б)	,
	в)	,	г)	.
15.	а)	,	б)	,
	в)	,	г)	.
16.	а)	,	б)	,
	в)	,	г)	.
17.	а)	,	б)	,
	в)	,	г)	.
18.	а)	,	б)	,
	в)	,	г)	.
19.	а)	,	б)	,
	в)	,	г)	.
20.	а)	,	б)	,
	в)	,	г)	.

31.	,	,	,	.
32.	,	,	,	.
33.	,	,	,	.
34.	,	,	,	.
35.	,	,	,	.
36.	,	,	,	.
37.	,	,	,	.
38.	,	,	,	.
39.	,	,	,	.
40.	,	,	,	.

41.	,	,	.
42.	,	,	.
43.	,	,	.
44.	,	,	.
45.	,	,	.
46.	,	,	.
47.	,	,	.
48.	,	,	.
49.	,	,	.
50.	,	,	.

51.	,	,	,	.
52.	,	,	,	.
53.	,	,	,	.
54.	,	,	,	.
55.	,	,	,	.
56.	,	,	,	.
57.	,	,	,	.
58.	,	,	,	.
59.	,	,	,	.
60.	,	,	,	.

61.	,	,	.
62.	,	,	.
63.	,	,	.
64.	,	,	.
65.	,	,	.
66.	,	,	.
67.	,	,	.
68.	,	,	.
69.	,	,	.
70.	,	,	.

71.	, .	72.	, .
73.	, .	74.	, .
75.	, .	76.	, .
77.	, .	78.	, .
79.	, .	80.	, .

81.	, .	82.	, .
83.	, .	84.	, .
85.	, .	86.	, .
87.	, .	88.	, .
89.	, .	90.	, .

11.	а)	,	б)	,
	в)	,	г)	.
12.	а)	,	б)	,
	в)	,	г)	.
13.	а)	,	б)	,
	в)	,	г)	.
14.	а)	,	б)	,
	в)	,	г)	.
15.	а)	,	б)	,
	в)	,	г)	.
16.	а)	,	б)	,
	в)	,	г)	.
17.	а)	,	б)	,
	в)	,	г)	.
18.	а)	,	б)	,
	в)	,	г)	.
19.	а)	,	б)	,
	в)	,	г)	.
20.	а)	,	б)	,
	в)	,	г)	.

31.	,	,	,	.
32.	,	,	,	.
33.	,	,	,	.
34.	,	,	,	.
35.	,	,	,	.
36.	,	,	,	.
37.	,	,	,	.
38.	,	,	,	.
39.	,	,	,	.
40.	,	,	,	.

41.	,	,	.
42.	,	,	.
43.	,	,	.
44.	,	,	.
45.	,	,	.
46.	,	,	.
47.	,	,	.
48.	,	,	.
49.	,	,	.
50.	,	,	.

51.	,	,	,	.
52.	,	,	,	.
53.	,	,	,	.
54.	,	,	,	.
55.	,	,	,	.
56.	,	,	,	.
57.	,	,	,	.
58.	,	,	,	.
59.	,	,	,	.
60.	,	,	,	.

61.	,	,	.
62.	,	,	.
63.	,	,	.
64.	,	,	.
65.	,	,	.
66.	,	,	.
67.	,	,	.
68.	,	,	.
69.	,	,	.
70.	,	,	.

71.	, .	72.	, .
73.	, .	74.	, .
75.	, .	76.	, .
77.	, .	78.	, .
79.	, .	80.	, .

81.	, .	82.	, .
83.	, .	84.	, .
85.	, .	86.	, .
87.	, .	88.	, .
89.	, .	90.	, .

11.	а)	,	б)	,
	в)	,	г)	.
12.	а)	,	б)	,
	в)	,	г)	.
13.	а)	,	б)	,
	в)	,	г)	.
14.	а)	,	б)	,
	в)	,	г)	.
15.	а)	,	б)	,
	в)	,	г)	.
16.	а)	,	б)	,
	в)	,	г)	.
17.	а)	,	б)	,
	в)	,	г)	.
18.	а)	,	б)	,
	в)	,	г)	.
19.	а)	,	б)	,
	в)	,	г)	.
20.	а)	,	б)	,
	в)	,	г)	.

31.	,	,	,	.
32.	,	,	,	.
33.	,	,	,	.
34.	,	,	,	.
35.	,	,	,	.
36.	,	,	,	.
37.	,	,	,	.
38.	,	,	,	.
39.	,	,	,	.
40.	,	,	,	.

41.	,	,	.
42.	,	,	.
43.	,	,	.
44.	,	,	.
45.	,	,	.
46.	,	,	.
47.	,	,	.
48.	,	,	.
49.	,	,	.
50.	,	,	.

51.	,	,	,	.
52.	,	,	,	.
53.	,	,	,	.
54.	,	,	,	.
55.	,	,	,	.
56.	,	,	,	.
57.	,	,	,	.
58.	,	,	,	.
59.	,	,	,	.
60.	,	,	,	.

61.	,	,	.
62.	,	,	.
63.	,	,	.
64.	,	,	.
65.	,	,	.
66.	,	,	.
67.	,	,	.
68.	,	,	.
69.	,	,	.
70.	,	,	.

71.	, .	72.	, .
73.	, .	74.	, .
75.	, .	76.	, .
77.	, .	78.	, .
79.	, .	80.	, .

81.	, .	82.	, .
83.	, .	84.	, .
85.	, .	86.	, .
87.	, .	88.	, .
89.	, .	90.	, .