I реалізація
Випадкові коефіцієнти Vν (ν=4..10):
ν |
ξ1 |
ξ2 |
k |
Ckν |
C(k+1)ν |
Vν |
4 |
0,08 |
0,30 |
1 |
-5,28 |
-3,25 |
-4,6794 |
5 |
0,08 |
0,50 |
1 |
-5,72 |
-2,15 |
-3,9225 |
6 |
0,37 |
0,75 |
2 |
-3,58 |
-0,61 |
-1,3596 |
7 |
0,23 |
0,14 |
2 |
-2,33 |
-0,53 |
-2,0811 |
8 |
0,96 |
0,56 |
5 |
2,21 |
7,24 |
5,0017 |
9 |
0,07 |
0,18 |
1 |
-7,37 |
-2,64 |
-6,4959 |
10 |
0,78 |
0,57 |
4 |
1,55 |
2,54 |
2,1120 |
3-кратне перетворення математичного чекання:
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
m(1)(i) |
22,7652 |
23,8895 |
24,1324 |
25,8871 |
24,9109 |
24,8792 |
24,8760 |
23,6447 |
23,9047 |
23,7351 |
m(2)(i) |
22,7652 |
20,4046 |
22,6896 |
26,3296 |
23,7957 |
24,2414 |
25,3500 |
23,6028 |
23,6747 |
23,8849 |
m(3)(i) |
22,7652 |
20,4046 |
28,9492 |
26,7365 |
25,2855 |
23,3776 |
23,6223 |
22,3572 |
22,4541 |
24,0539 |
Перша реалізація апостеріорного
випадкового процесу
:
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
x(3)(i) |
22,7652 |
20,4046 |
28,9492 |
22,0571 |
21,9807 |
21,9709 |
23,1946 |
27,0977 |
17,1675 |
25,5244 |
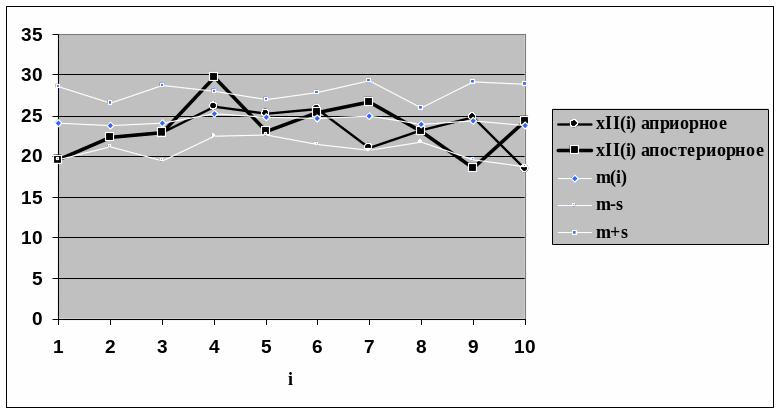
Перша реалізація апріорного і апостеріорного випадкових процесів + довірчий інтервал (графік):
II реалізація
Випадкові коефіцієнти Vν (ν=4..10):
ν |
ξ1 |
ξ2 |
k |
Ckν |
C(k+1)ν |
Vν |
4 |
0,66 |
0,72 |
4 |
1,27 |
2,78 |
2,3592 |
5 |
0,23 |
0,63 |
2 |
-2,15 |
-0,48 |
-1,1052 |
6 |
0,51 |
0,37 |
3 |
-0,61 |
0,96 |
-0,0295 |
7 |
0,70 |
0,50 |
4 |
0,99 |
2,62 |
1,8038 |
8 |
0,52 |
0,38 |
3 |
-0,73 |
1,12 |
-0,0251 |
9 |
0,17 |
0,59 |
1 |
-7,37 |
-2,64 |
-4,5627 |
10 |
0,50 |
0,25 |
3 |
-0,75 |
1,55 |
-0,1748 |
3-кратне перетворення математичного чекання:
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
m(1)(i) |
19,5395 |
23,9088 |
24,2227 |
27,2709 |
25,1818 |
25,3953 |
24,4631 |
22,9382 |
22,8306 |
23,4996 |
m(2)(i) |
19,5395 |
22,4203 |
23,6064 |
27,4599 |
24,7055 |
25,1229 |
24,6656 |
22,9204 |
22,7323 |
23,5636 |
m(3)(i) |
19,5395 |
22,4203 |
22,8905 |
27,4134 |
24,5351 |
25,2217 |
24,8632 |
23,0628 |
22,8719 |
23,5443 |
Друга реалізація апостеріорного
випадкового процесу
:
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
x(3)(i) |
19,5395 |
22,4203 |
22,8905 |
29,7726 |
23,1184 |
25,3885 |
26,7942 |
23,1571 |
18,6007 |
24,3390 |
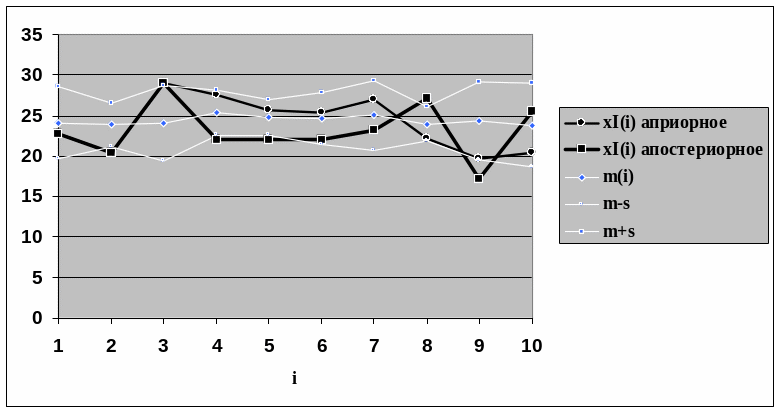
Д
руга
реалізація апріорного і апостеріорного
випадкових процесів + довірчий інтервал
(графік):
