Висновок
У результаті виконання завдання №3 я навчився обчислювати елементи канонічного зображення апріорного випадкового процесу.
в
)
Завдання №4.
Отримання елементів канонічного зображення апостеріорного випадкового процесу.
Індивідуальне прогнозування надійності
Загальні теоретичні положення
Отримання елементів канонічного зображення апостеріорного випадкового процесу
Обробка статистичних даних і одержання математичного опису випадкового процесу X(t) складають зміст першого етапу розв'язання задачі прогнозу. Він реалізується до проведення контролю (до досліду), тому всю інформацію, що використовується на цьому етапі, вважають апріорною. Згідно з цим і процес X(t), який вивчають на цьому етапі, називають апріорним.
Наявність математичного опису апріорного випадкового процесу дозволяє перейти до другого етапу розв'язання задачі прогцозу. На цьому етапі одержують математичний опис апостеріорного випадкового процесу X(t), що враховує результати контролю.
Канонічне зображення апостеріорного випадкового процесу для k моментів контролю:
Математичне чекання апостеріорного випадкового процесу при k моментах контролю:
Згідно з цим на першому етапі відбувається k-кратне перетворення математичного чекання, а потім знаходження елементів канонічного зображення апостеріорного випадкового процесу для k моментів контролю.
У цій курсовій роботі кількість моментів контролю параметра при апостеріорному прогнозі k=3.
Апостеріорний процес на ділянці i<k вироджується в детермінований. Для k<і<І можна відмітити значно менший розбіг апостеріорного випадкового процесу порівняно з апріорним.
Дисперсія апостеріорного випадкового процесу може бути оцінена так:
.
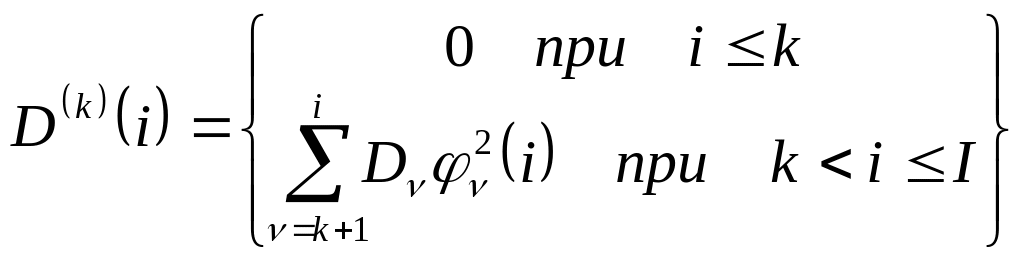В області прогнозу i>k справедлива умова:
D(k)(i)≤D(i), k<i≤I.
Дисперсія апостеріорного процесу буде одночасно мірою точності передбачення майбутнього технічного стану об'єкта, оскільки вона в цьому випадку визначає можливе розсіювання справжніх траекторій процесу відносно передбаченого значення. З цієї точки зору наведена вище нерівність може бути використована для оцінки ефективності прогнозу. Якщо апостеріорна дисперсія менше апріорної, то прогноз досить ефективний.
Прогнозування надійності
Оцінку спрогнозованої надійності контрольованого об'єкта можна проводити методом Монте-Карло.
Кожне обчислене значення x(k)(i), k+1≤i≤I для кожної реалізації порівнюється із границями допуску [a,b]. Якщо при деякому і значення реалізації вийшло за межі допуску, то фіксується відмова об'єкта й додається одиниця до лічильника кількості відмов qi, k+1≤i≤I.
Після того, як будуть проконтрольовані всі N=3 реалізації, прогнозована надійність обчислюється по формулі:
,
k+1≤i≤I.
Вихідні дані
В якості вихідних даних для цього завдання використати дані завдання №3.
Рішення завдання
Розрахункові формули:
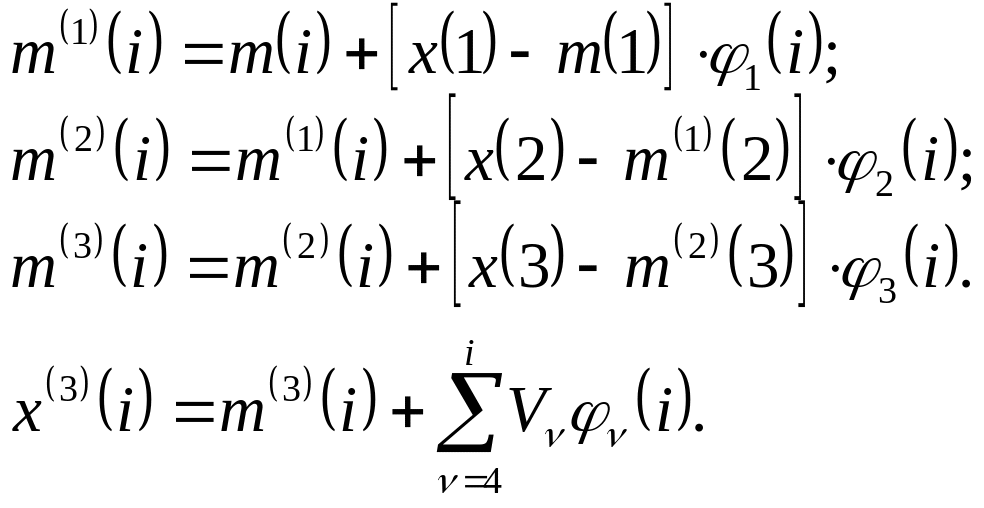
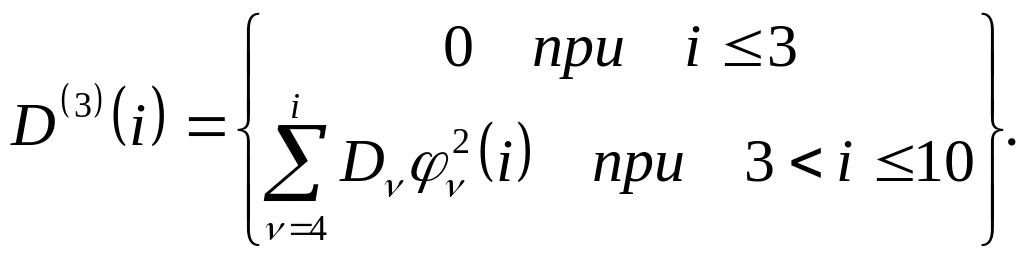
Всі розрахунки у цьому завданні проводяться на ЕОМ в програмі Microsof Excel із пакета Microsoft Office. (Для генерування випадкових чисел ξ1 і ξ2 використовується функція СЛЧИС().) Тому результати розрахунків дуже зручно оформлювати у вигляді таблиць.