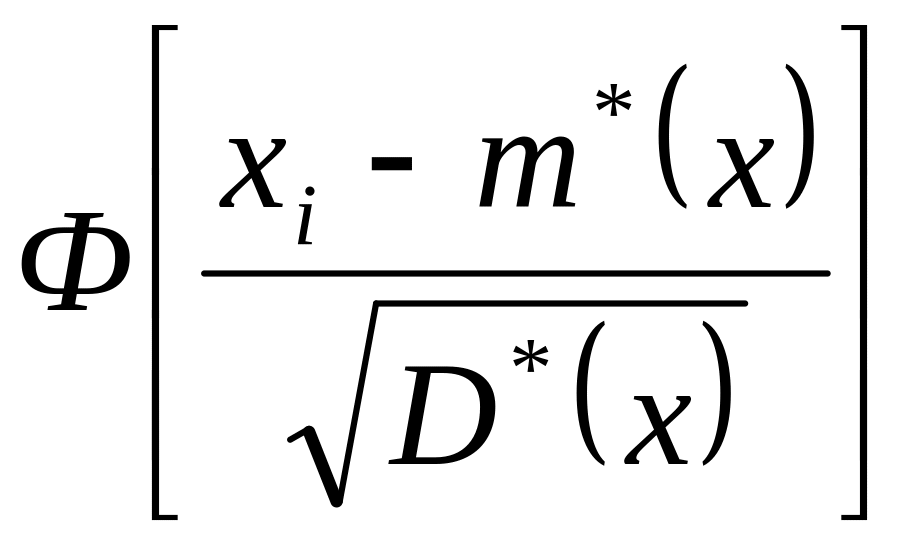Рішення завдання
1) Випадкова величина розташовується в порядку зростання, створюючи варіаційний ряд:
17,83 |
20,05 |
21,27 |
22,38 |
23,3 |
24,27 |
25,41 |
26,29 |
27,4 |
28,97 |
18,47 |
20,12 |
21,28 |
22,51 |
23,3 |
24,35 |
25,42 |
26,33 |
27,44 |
29,06 |
18,51 |
20,13 |
21,33 |
22,52 |
23,34 |
24,43 |
25,45 |
26,34 |
27,44 |
29,18 |
18,52 |
20,15 |
21,34 |
22,53 |
23,34 |
24,47 |
25,47 |
26,41 |
27,45 |
29,2 |
18,55 |
20,19 |
21,34 |
22,56 |
23,51 |
24,5 |
25,48 |
26,45 |
27,55 |
29,22 |
18,62 |
20,22 |
21,42 |
22,59 |
23,53 |
24,54 |
25,51 |
26,46 |
27,66 |
29,29 |
18,65 |
20,24 |
21,45 |
22,6 |
23,59 |
24,6 |
25,54 |
26,5 |
27,69 |
29,4 |
18,69 |
20,24 |
21,46 |
22,6 |
23,76 |
24,61 |
25,55 |
26,5 |
27,74 |
29,41 |
18,71 |
20,24 |
21,49 |
22,69 |
23,77 |
24,62 |
25,58 |
26,52 |
27,8 |
29,51 |
18,72 |
20,3 |
21,49 |
22,77 |
23,78 |
24,65 |
25,58 |
26,62 |
27,88 |
29,58 |
18,87 |
20,35 |
21,61 |
22,78 |
23,82 |
24,65 |
25,62 |
26,63 |
27,91 |
29,68 |
18,9 |
20,37 |
21,75 |
22,8 |
23,9 |
24,75 |
25,62 |
26,66 |
27,93 |
29,76 |
18,94 |
20,43 |
21,83 |
22,8 |
23,92 |
24,93 |
25,66 |
26,66 |
27,99 |
29,78 |
18,97 |
20,57 |
21,83 |
22,8 |
23,95 |
24,99 |
25,67 |
26,68 |
28,09 |
29,79 |
19,07 |
20,6 |
21,84 |
22,89 |
23,95 |
25,04 |
25,72 |
26,73 |
28,29 |
29,83 |
19,16 |
20,76 |
21,87 |
22,9 |
23,98 |
25,06 |
25,73 |
26,74 |
28,35 |
29,84 |
19,22 |
20,89 |
21,89 |
22,95 |
24,02 |
25,08 |
25,79 |
26,77 |
28,4 |
29,93 |
19,29 |
20,93 |
21,94 |
22,98 |
24,02 |
25,08 |
25,81 |
26,81 |
28,41 |
30,07 |
19,42 |
20,98 |
21,95 |
23,01 |
24,05 |
25,1 |
25,82 |
26,82 |
28,41 |
30,17 |
19,43 |
21,03 |
21,97 |
23,02 |
24,05 |
25,11 |
25,83 |
26,84 |
28,44 |
30,23 |
19,45 |
21,05 |
22,03 |
23,03 |
24,08 |
25,13 |
25,85 |
26,91 |
28,45 |
30,49 |
19,66 |
21,09 |
22,07 |
23,08 |
24,11 |
25,13 |
25,87 |
26,95 |
28,56 |
30,52 |
19,68 |
21,16 |
22,13 |
23,1 |
24,12 |
25,14 |
25,93 |
27,03 |
28,58 |
30,67 |
19,69 |
21,17 |
22,13 |
23,11 |
24,17 |
25,22 |
25,94 |
27,03 |
28,58 |
30,77 |
19,77 |
21,2 |
22,19 |
23,13 |
24,19 |
25,22 |
25,96 |
27,17 |
28,65 |
30,83 |
19,8 |
21,22 |
22,21 |
23,18 |
24,24 |
25,26 |
26,02 |
27,21 |
28,82 |
30,86 |
19,82 |
21,22 |
22,25 |
23,19 |
24,25 |
25,35 |
26,08 |
27,22 |
28,84 |
31,05 |
19,84 |
21,23 |
22,26 |
23,27 |
24,25 |
25,35 |
26,13 |
27,24 |
28,84 |
31,07 |
19,85 |
21,25 |
22,28 |
23,28 |
24,26 |
25,36 |
26,24 |
27,32 |
28,86 |
31,15 |
20,02 |
21,27 |
22,3 |
23,3 |
24,26 |
25,36 |
26,28 |
27,34 |
28,89 |
31,52 |
2) Знаходимо розмах варіювання:
3) Розділимо розмах варіювання на f=15 інтервалів і визначимо ширину кожного інтервалу:
,
де i=1..f – номер інтервалу.
Отримуємо наступні інтервали:
номер інтервалу i |
границі інтервалу |
|
1 |
17,83 |
18,7427 |
2 |
18,7427 |
19,6553 |
3 |
19,6553 |
20,568 |
4 |
20,568 |
21,4807 |
5 |
21,4807 |
22,3933 |
6 |
22,3933 |
23,306 |
7 |
23,306 |
24,2187 |
8 |
24,2187 |
25,1313 |
9 |
25,1313 |
26,044 |
10 |
26,044 |
26,9567 |
11 |
26,9567 |
27,8693 |
12 |
27,8693 |
28,782 |
13 |
28,782 |
29,6947 |
14 |
29,6947 |
30,6073 |
15 |
30,6073 |
31,52 |
4) Знаходимо
кількість значень випадкової величини,
що потрапили в кожний i-ий інтервал (fi),
визначаємо статистичну частоту влучення
для кожного інтервалу
й складаємо таблицю:
інтервал i |
|
|
|
1 |
10 |
0,0333 |
0,0365 |
2 |
11 |
0,0367 |
0,0402 |
3 |
22 |
0,0733 |
0,0804 |
4 |
25 |
0,0833 |
0,0913 |
5 |
23 |
0,0767 |
0,084 |
6 |
31 |
0,1033 |
0,1132 |
7 |
23 |
0,0767 |
0,084 |
8 |
27 |
0,09 |
0,0986 |
9 |
34 |
0,1133 |
0,1242 |
10 |
26 |
0,0867 |
0,095 |
11 |
17 |
0,0567 |
0,0621 |
12 |
16 |
0,0533 |
0,0584 |
13 |
16 |
0,0533 |
0,0584 |
14 |
11 |
0,0367 |
0,0402 |
15 |
8 |
0,0267 |
0,0292 |
5
)
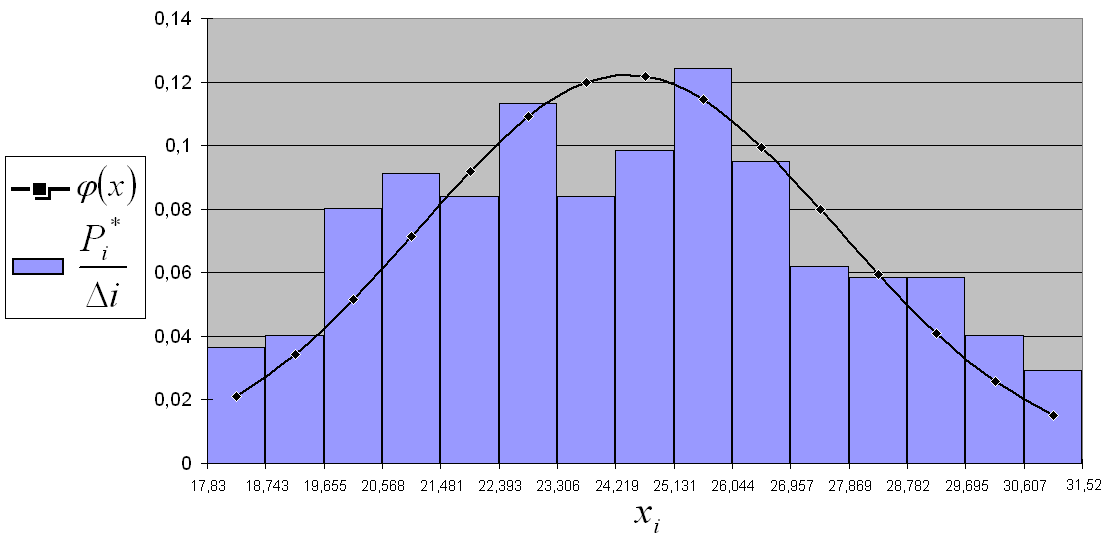
Будуємо гістограму: на
осі абсцис відзначаємо границі інтервалів,
на кожному інтервалі будуємо прямокутник
заввишки
.
Площа кожного прямокутника дорівнює
,
загальна площа всіх прямокутників
гістограми дорівнює 1.
Гістограма:
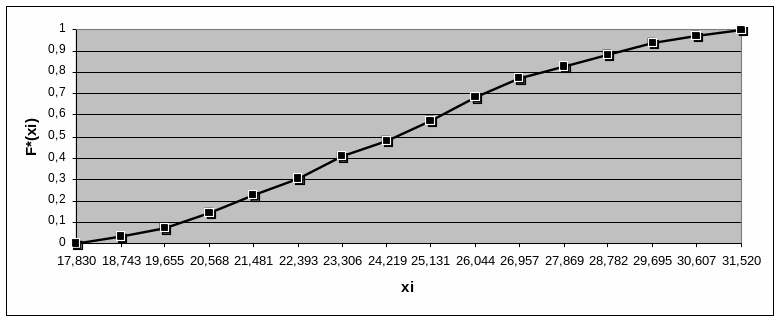
6) Будуємо статистичну функцію розподілу по даним гістограми:
i |
|
|
1 |
17,83 |
0 |
2 |
18,7427 |
0,0333 |
3 |
19,6553 |
0,07 |
4 |
20,568 |
0,1433 |
5 |
21,4807 |
0,2267 |
6 |
22,3933 |
0,3033 |
7 |
23,306 |
0,4067 |
8 |
24,2187 |
0,4833 |
9 |
25,1313 |
0,5733 |
10 |
26,044 |
0,6867 |
11 |
26,9567 |
0,7733 |
12 |
27,8693 |
0,83 |
13 |
28,782 |
0,8833 |
14 |
29,6947 |
0,9367 |
15 |
30,6073 |
0,9733 |
16 |
31,52 |
1 |
Статистична функція розподілу:
7) Для кожного i-ого інтервалу знаходимо теоретичну ймовірність того, що параметр прийме яке-небудь значення з i-ого інтервалу:
де xiв, xiн – верхні й нижні границі інтервалів, математичне чекання m*(x)= 24,4046, дисперсія D*(x)= 10,6532 (див. завдання №1), Ф(x) – функція Лапласа (див. додаток №1);
а також теоретичну функцію розподілу Fi:
і вносимо отримані результати в таблицю разом зі значеннями статистичних частот і статистичної функції розподілу :
i |
|
|
|
|
|
|
|
1 |
17,83 |
-2,0143 |
0,0228 |
0,019 |
0 |
0,0333 |
0 |
2 |
18,7427 |
-1,7347 |
0,0418 |
0,0303 |
0,019 |
0,0367 |
0,0333 |
3 |
19,6553 |
-1,4551 |
0,0721 |
0,0469 |
0,0493 |
0,0733 |
0,07 |
4 |
20,568 |
-1,1755 |
0,119 |
0,0651 |
0,0962 |
0,0833 |
0,1433 |
5 |
21,4807 |
-0,8958 |
0,1841 |
0,0835 |
0,1613 |
0,0767 |
0,2267 |
6 |
22,3933 |
-0,6162 |
0,2676 |
0,0993 |
0,2448 |
0,1033 |
0,3033 |
7 |
23,306 |
-0,3366 |
0,3669 |
0,1092 |
0,3441 |
0,0767 |
0,4067 |
8 |
24,2187 |
-0,057 |
0,4761 |
0,111 |
0,4533 |
0,09 |
0,4833 |
9 |
25,1313 |
0,2226 |
0,5871 |
0,1044 |
0,5643 |
0,1133 |
0,5733 |
10 |
26,044 |
0,5023 |
0,6915 |
0,0908 |
0,6687 |
0,0867 |
0,6867 |
11 |
26,9567 |
0,7819 |
0,7823 |
0,0731 |
0,7595 |
0,0567 |
0,7733 |
12 |
27,8693 |
1,0615 |
0,8554 |
0,0545 |
0,8326 |
0,0533 |
0,83 |
13 |
28,782 |
1,3411 |
0,9099 |
0,0375 |
0,8871 |
0,0533 |
0,8833 |
14 |
29,6947 |
1,6208 |
0,9474 |
0,0239 |
0,9246 |
0,0367 |
0,9367 |
15 |
30,6073 |
1,9004 |
0,9713 |
0,0148 |
0,9485 |
0,0267 |
0,9733 |
16 |
31,52 |
2,18 |
0,9861 |
|
0,9633 |
|
1 |
8) На одному графіку зображуємо статистичну F*(x) і теоретичну F(x) функції розподілу:
i |
xi |
F*(xi) |
F(xi) |
1 |
17,83 |
0 |
0 |
2 |
18,7427 |
0,0333 |
0,019 |
3 |
19,6553 |
0,07 |
0,0493 |
4 |
20,568 |
0,1433 |
0,0962 |
5 |
21,4807 |
0,2267 |
0,1613 |
6 |
22,3933 |
0,3033 |
0,2448 |
7 |
23,306 |
0,4067 |
0,3441 |
8 |
24,2187 |
0,4833 |
0,4533 |
9 |
25,1313 |
0,5733 |
0,5643 |
10 |
26,044 |
0,6867 |
0,6687 |
11 |
26,9567 |
0,7733 |
0,7595 |
12 |
27,8693 |
0,83 |
0,8326 |
13 |
28,782 |
0,8833 |
0,8871 |
14 |
29,6947 |
0,9367 |
0,9246 |
15 |
30,6073 |
0,9733 |
0,9485 |
16 |
31,52 |
1 |
0,9633 |
С
татистична
+ теоретична функції розподілу:
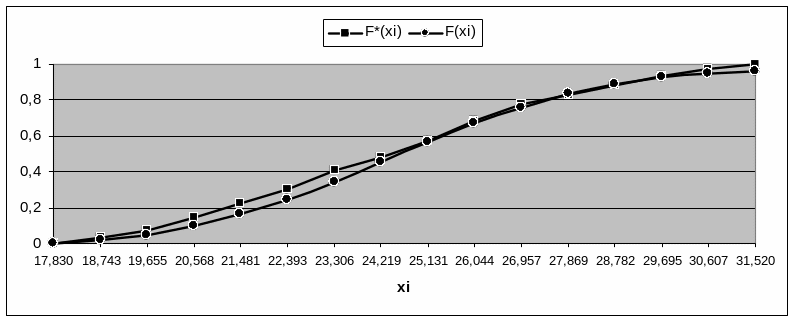
9) Визначаємо максимальну величину модуля різниці між F*(x) і F(x):
Rmax = max | F*(x) - F(x)| = | F*(21,4807) - F(21,4807) | = | 0,2267 - 0,1613 | = 0,0654.
10) Знаходимо допоміжну величину λ:
За таблицею критерію Колмогорова
(див. додаток №2) визначаємо ймовірність
P(λ)
того, що випадково максимальна розбіжність
між F*(x)
і F(x), помножена в
раз, може перевершити фіксоване λ:
P(λ) = P(1,1328) ≈ 0,16 > 0,1.
Отже, розподіл є нормальним: F*(x) не суперечить F(x).
11) Для згладжування гістограми будується теоретична функція щільності розподілу, у якості її аргументів візьмемо середини інтервалів:
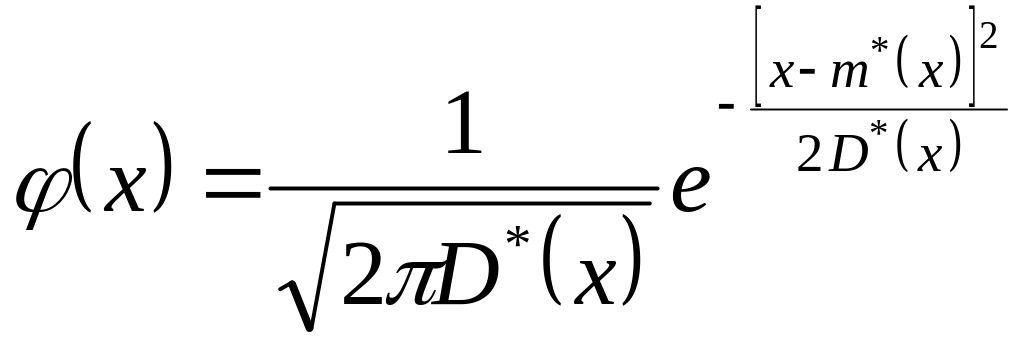
j |
xj |
φ(xj) |
1 |
18,2864 |
0,0211 |
2 |
19,199 |
0,0343 |
3 |
20,1117 |
0,0515 |
4 |
21,0244 |
0,0715 |
5 |
21,937 |
0,0918 |
6 |
22,8497 |
0,1091 |
7 |
23,7624 |
0,1199 |
8 |
24,675 |
0,1218 |
9 |
25,5877 |
0,1145 |
10 |
26,5004 |
0,0995 |
11 |
27,413 |
0,0799 |
12 |
28,3257 |
0,0594 |
13 |
29,2384 |
0,0408 |
14 |
30,151 |
0,0259 |
15 |
31,0637 |
0,0153 |
Гістограма + згладжуючий графік теоретичної функції щільності розподілу:
