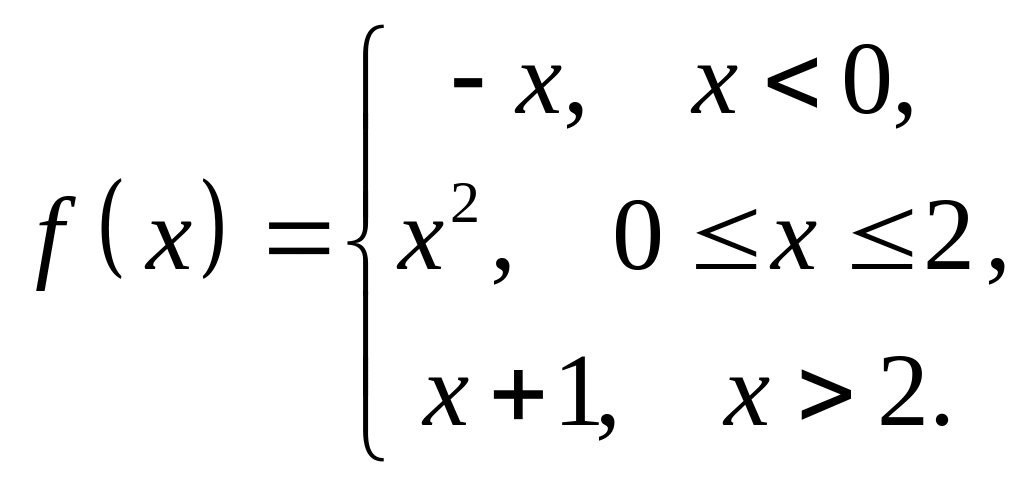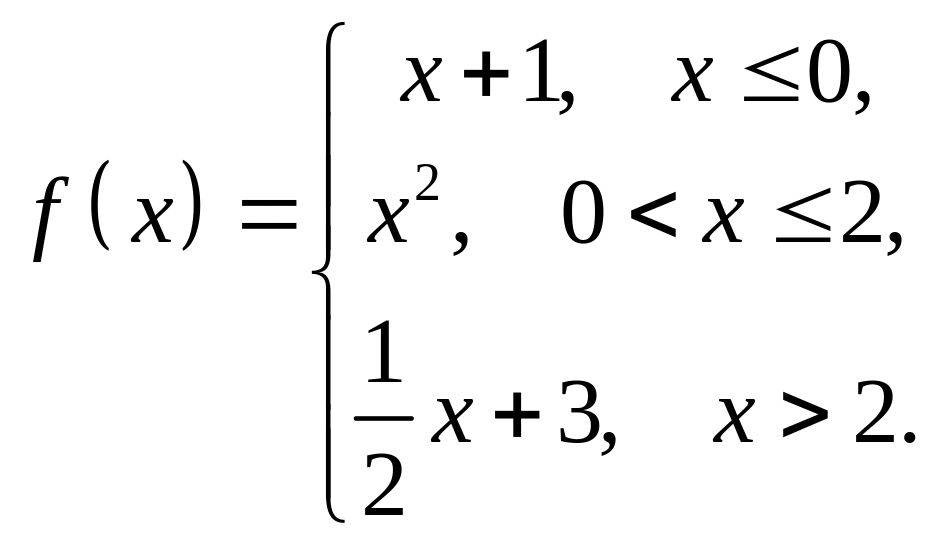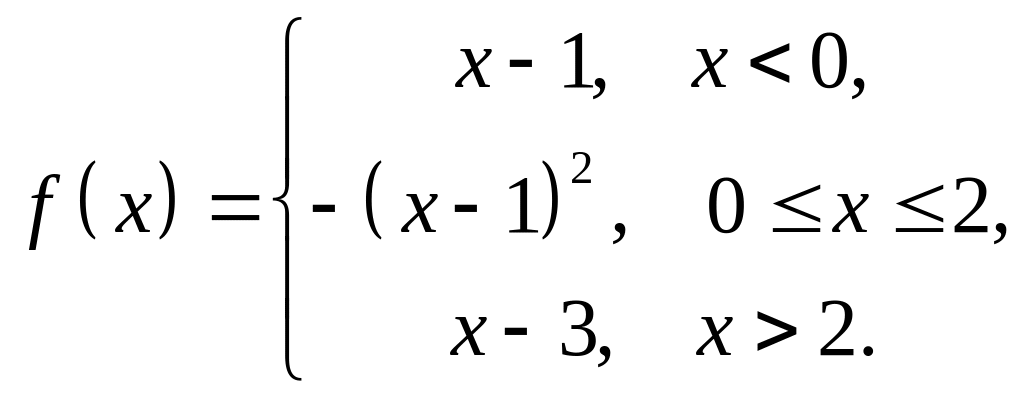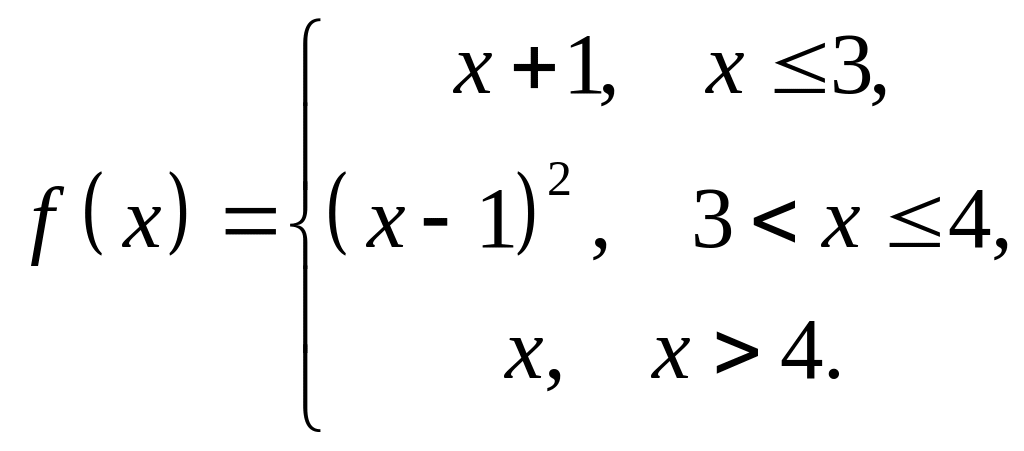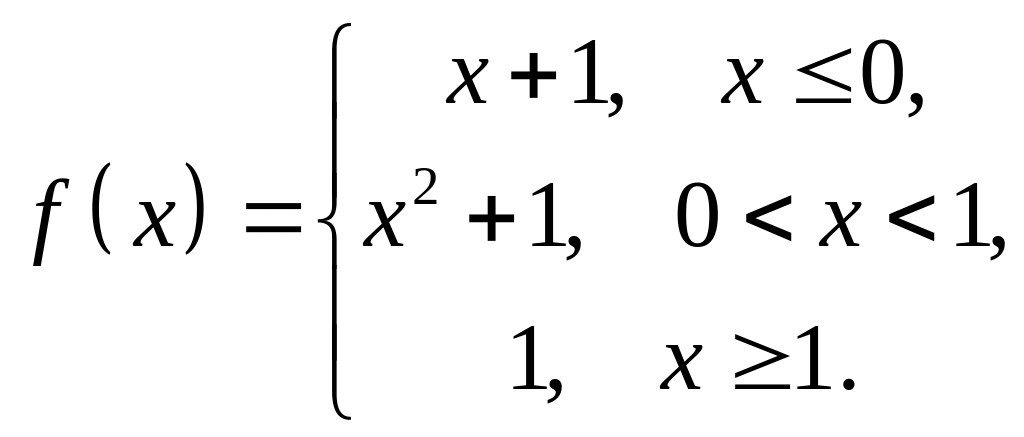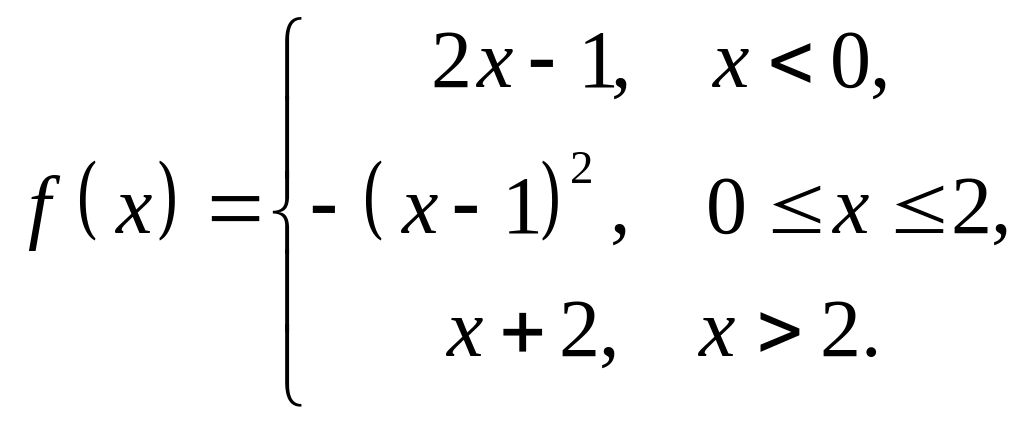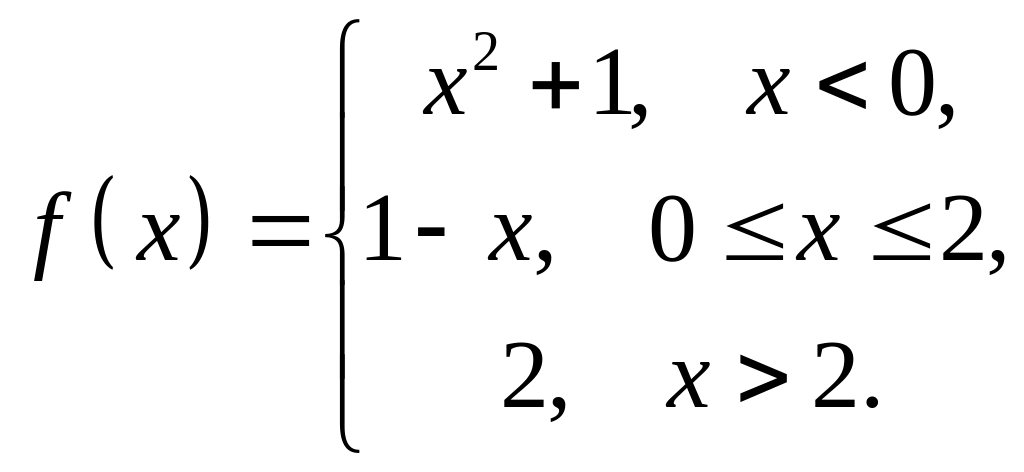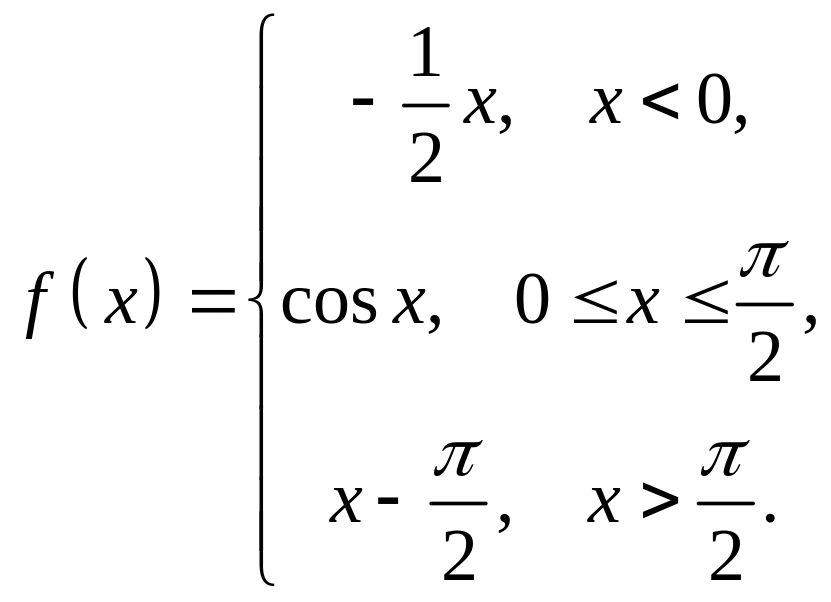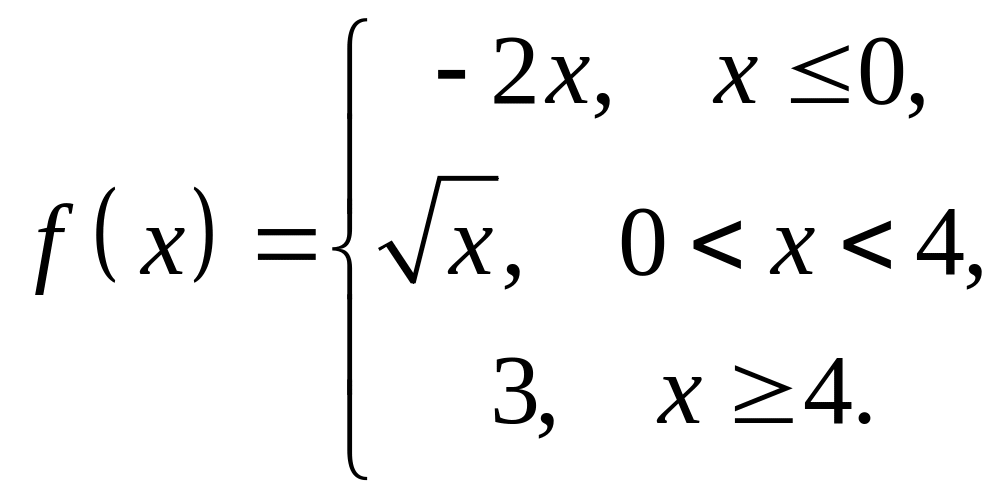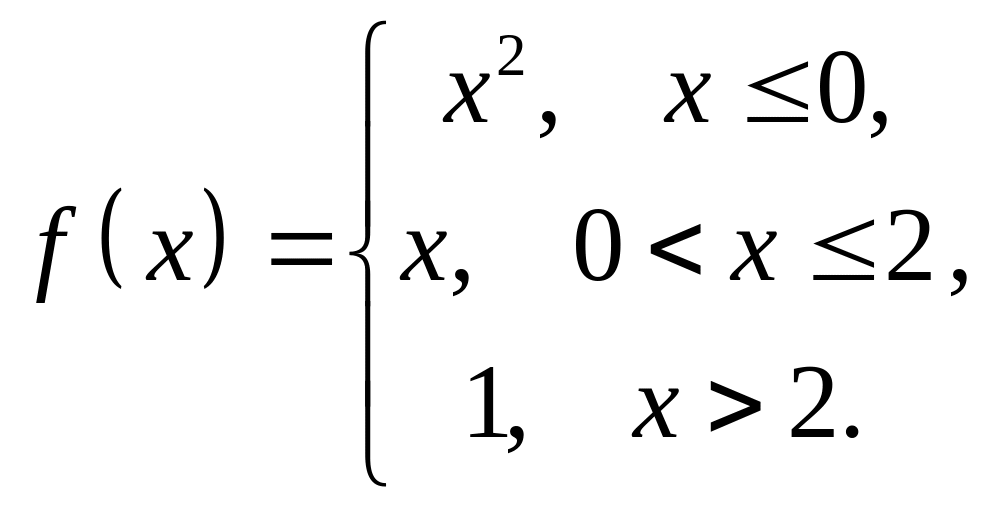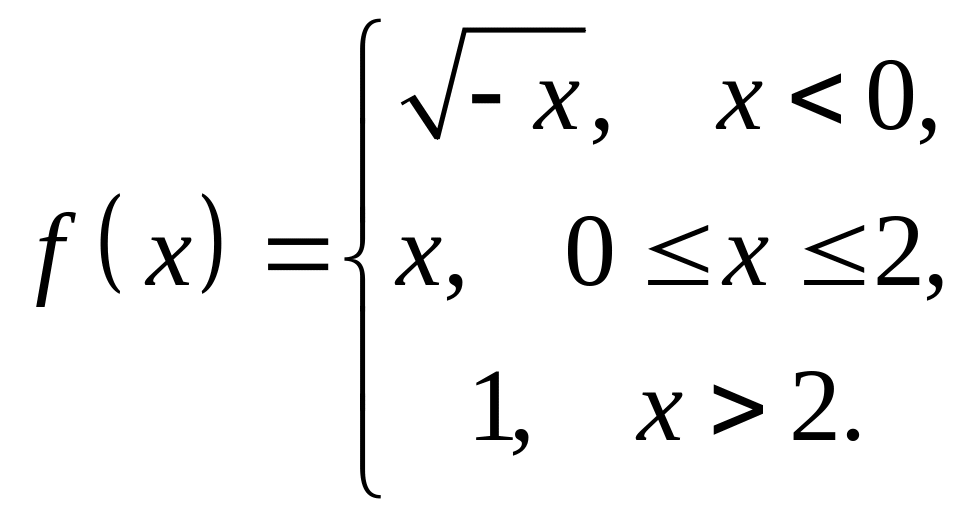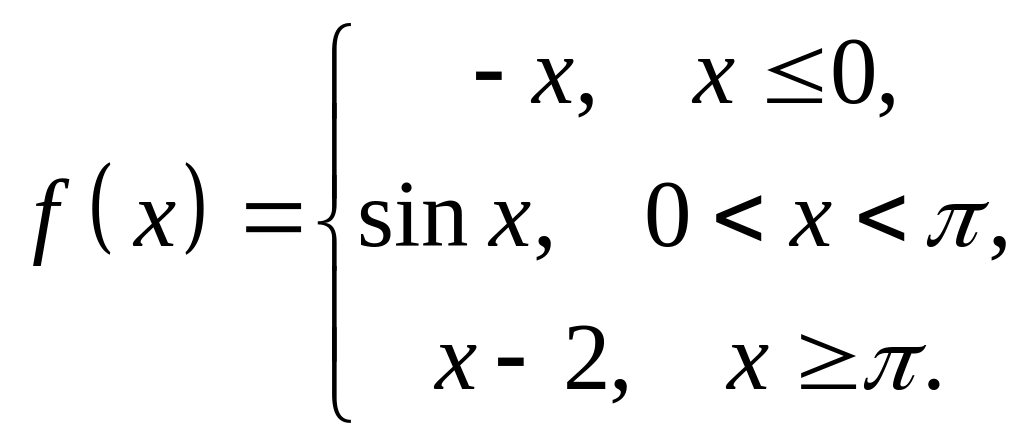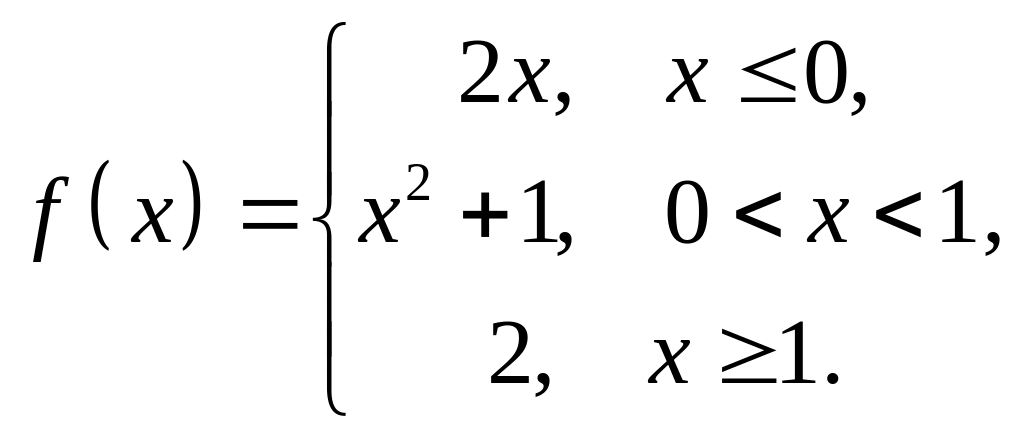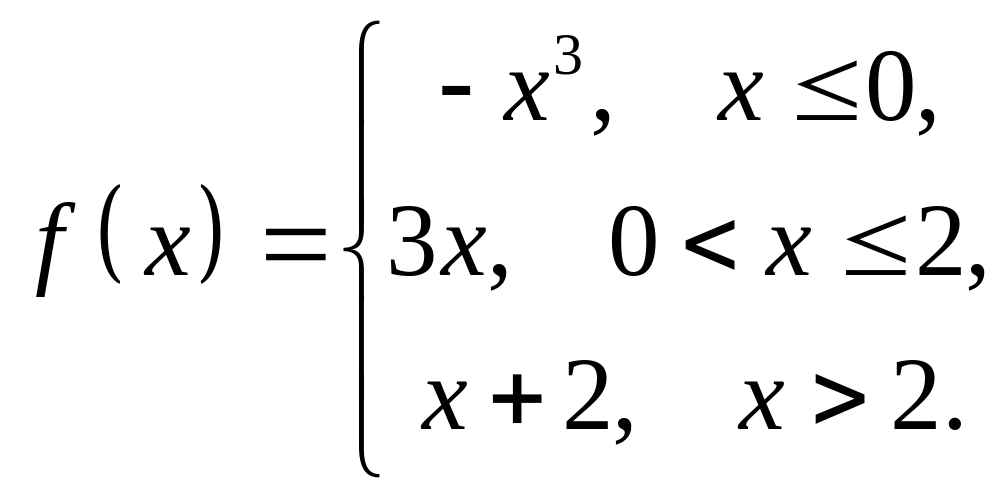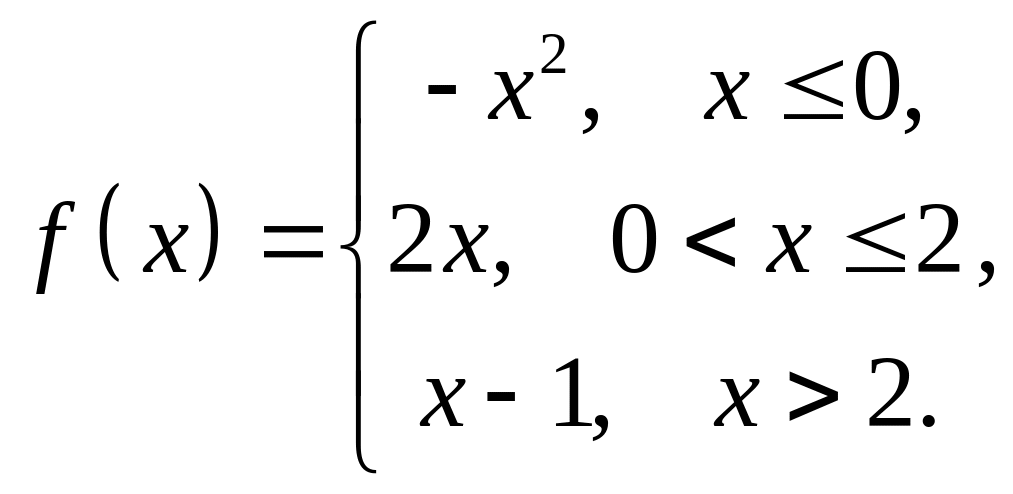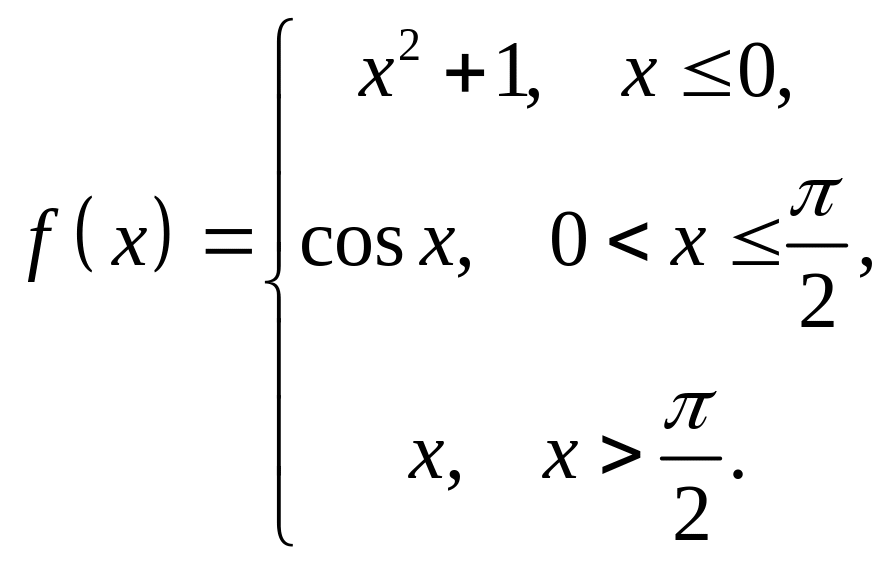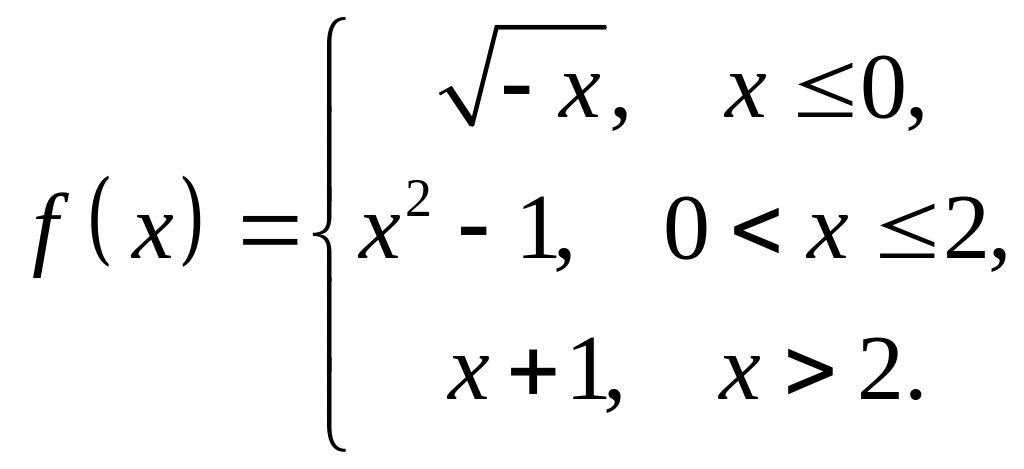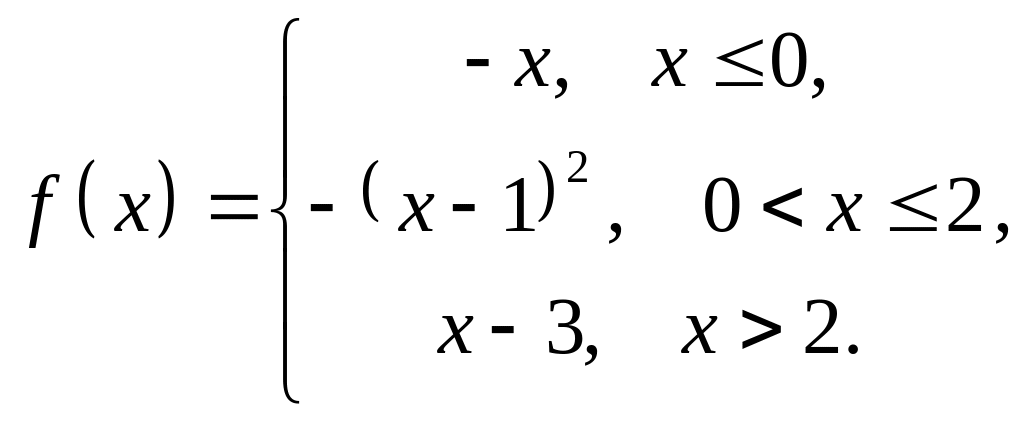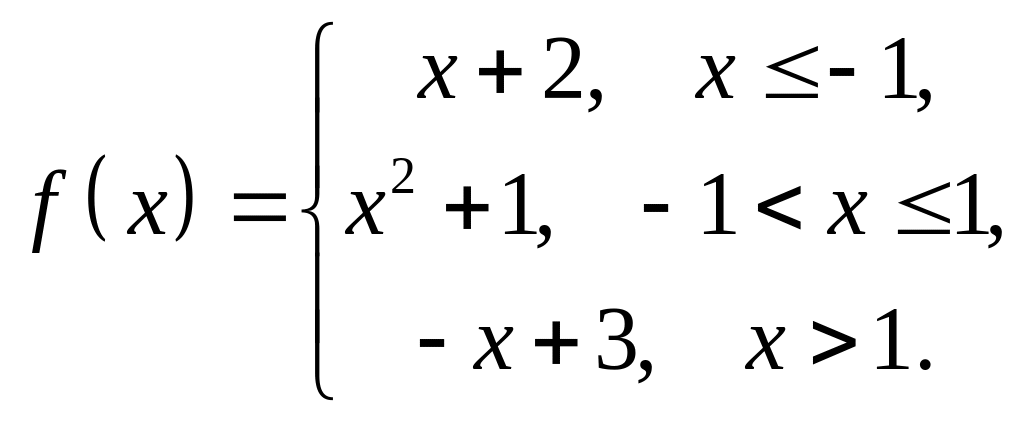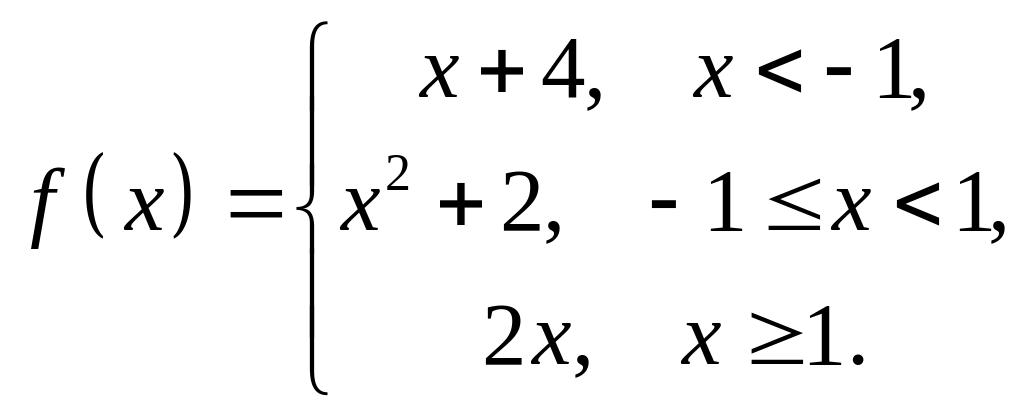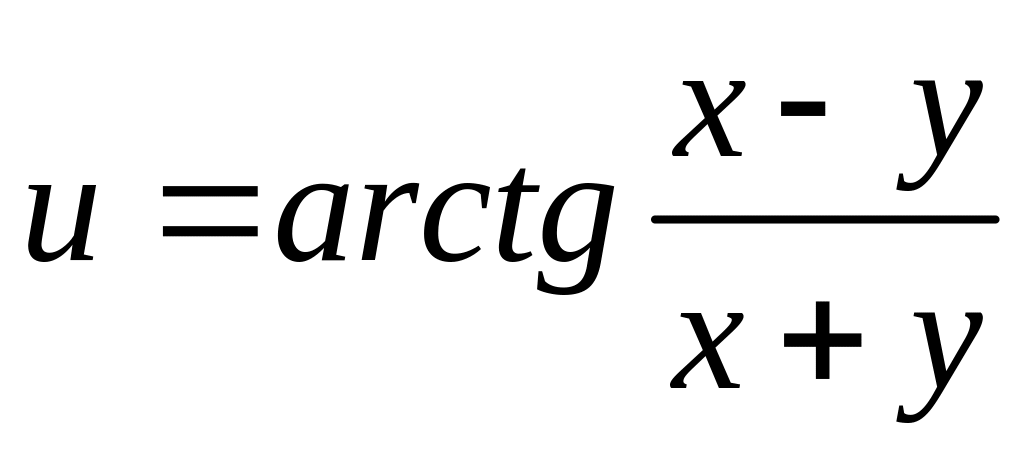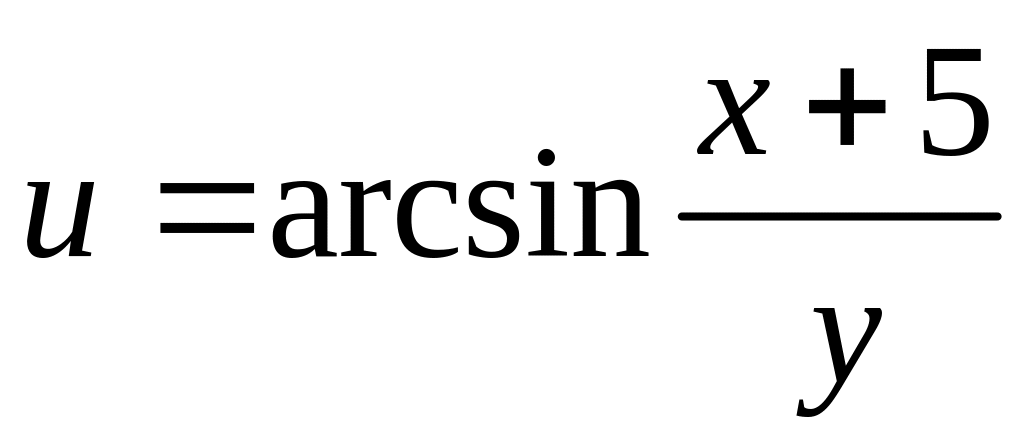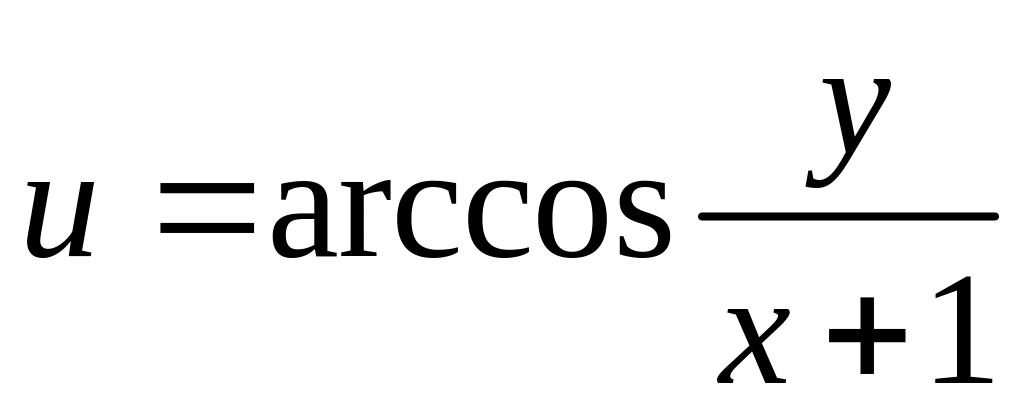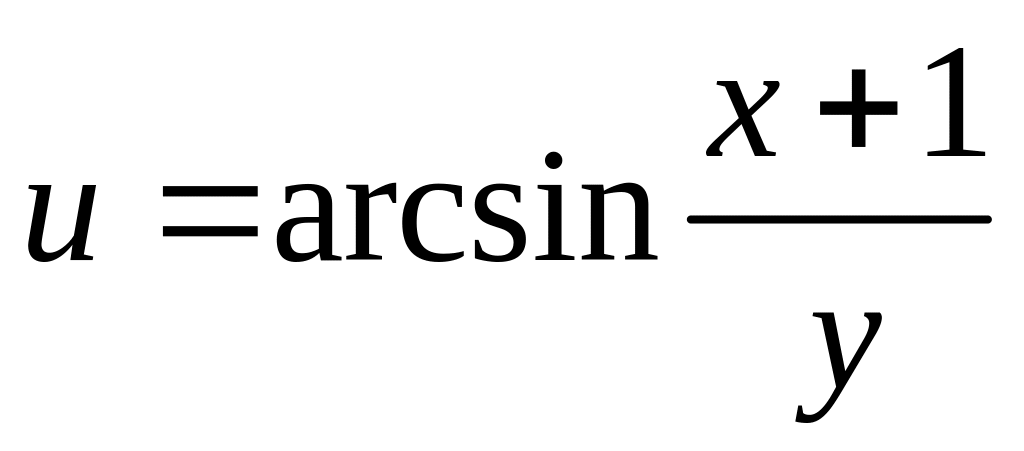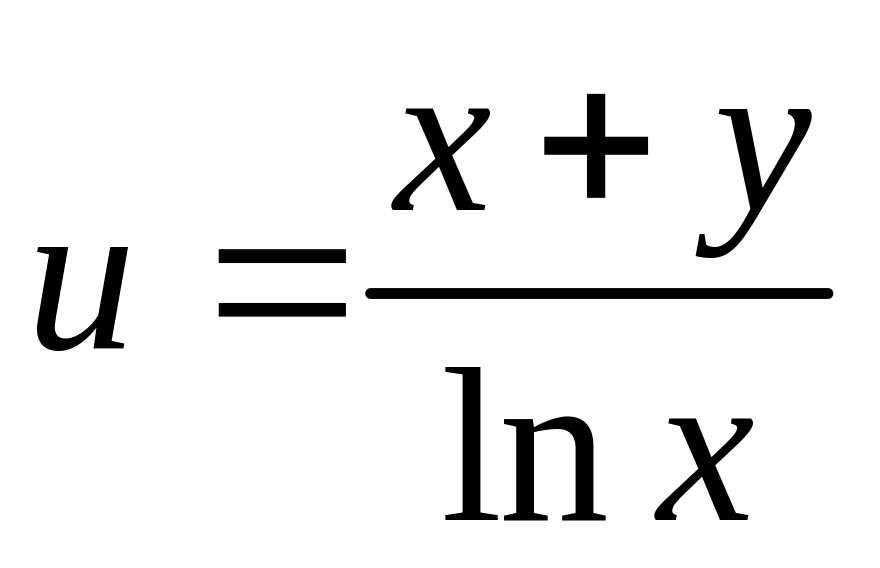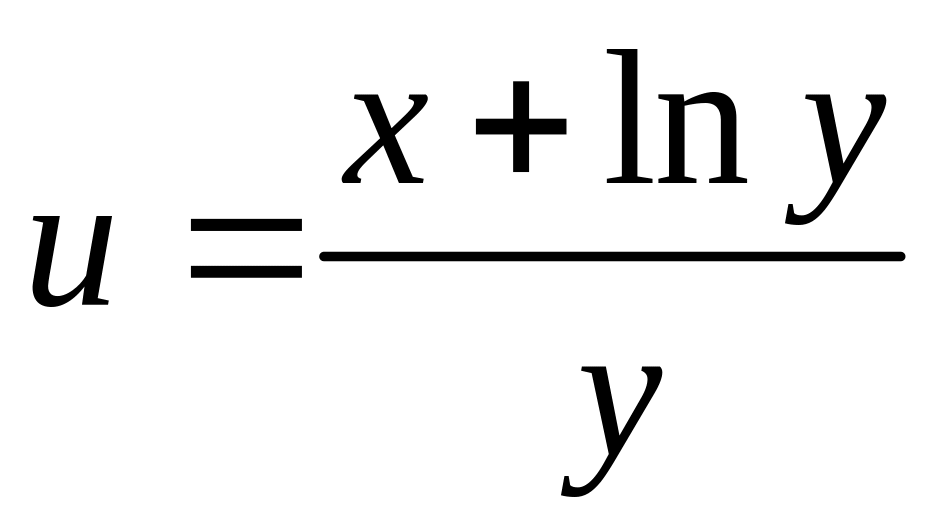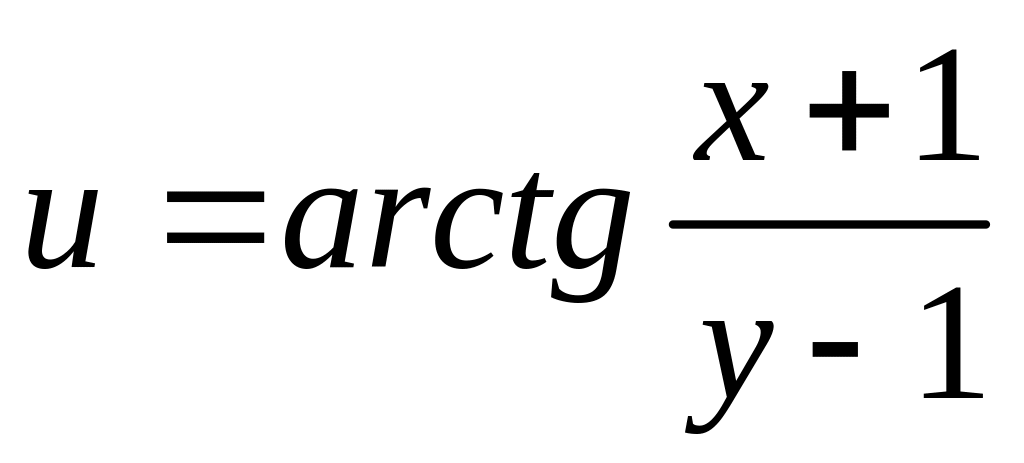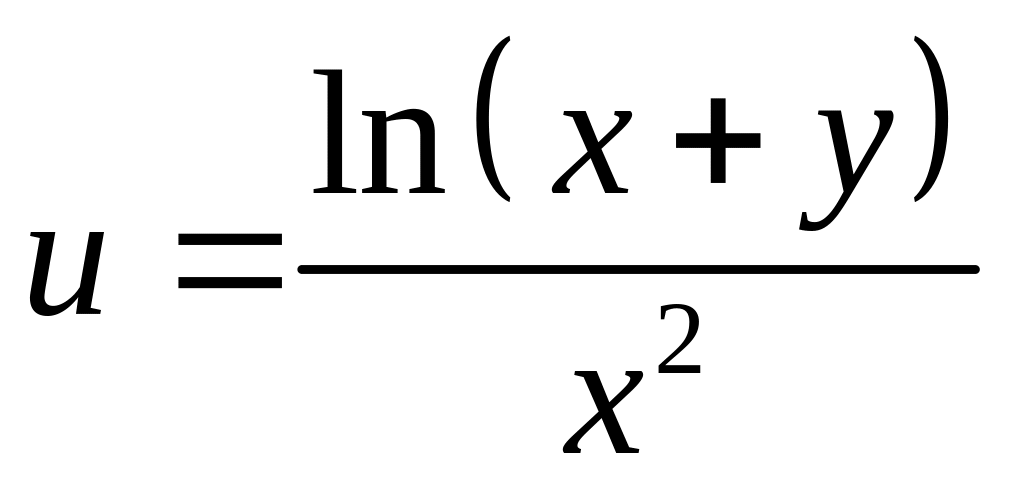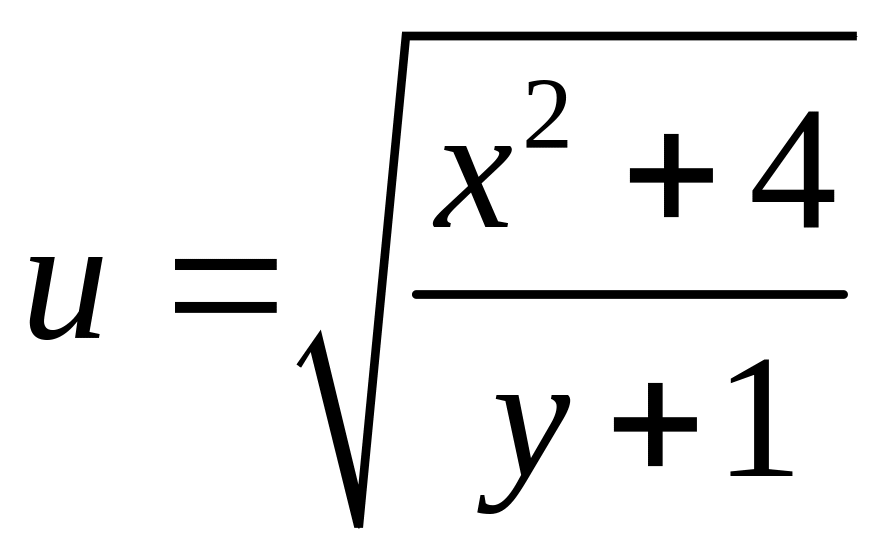- •« Могилевский государственный университет продовольствия»
- •Высшая математика
- •Рассмотрены и рекомендованы к изданию на заседании кафедры высшей математики
- •Требования к выполнению и оформлению контрольных работ
- •I Элементы линейной и векторной алгебры, аналитической геометрии
- •II Введение в математический анализ
- •III Дифференциальное исчисление функции одной переменной
- •Iy Функции нескольких переменных
- •Литература
- •Высшая математика
- •212027, Могилев, пр-т Шмидта, 3.
Министерство образования Республики Беларусь
Учреждение образования
« Могилевский государственный университет продовольствия»
Кафедра высшей математики
Высшая математика
Методические указания и задания
к контрольной работе № 1
для студентов-заочников технологических
специальностей
Могилев 2010
УДК 519.21 517
Рассмотрены и рекомендованы к изданию на заседании кафедры высшей математики
Протокол № 7 от 05. 02. 2010 г.
УМК по химико-технологическому
профилю специальностей
Протокол № 3 от 15. 02. 2010 г.
Составитель
канд.ф.-м. н., доцент В.К. Лапковский
Рецензент
канд.ф.-м. н., доцент А.М. Гальмак
Методические указания и контрольные задания соответствуют учебной программе «Высшая математика» для студентов-заочников технологических специальностей.
Они посвящены изучению тем: «Элементы линейной и векторной алгебры и аналитической геометрии», «Введение в математический анализ», «Дифференциальное исчисление функции одной переменной», «Применение дифференциального исчисления», «Функции нескольких переменных».
Методические указания содержат правила выполнения и оформления контрольных работ, задания контрольной работы № 1, примеры решения задач, вопросы для подготовки к экзамену и перечень рекомендуемой литературы.
УДК 519.21 517
© Учреждение образования
«Могилевский государственный
университет продовольствия», 2010
Требования к выполнению и оформлению контрольных работ
При оформлении контрольных работ надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для исправлений.
Контрольную работу следует выполнять в тетради, отдельной для каждой работы, чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента. Контрольная работа должна быть выполнена в рукописном виде.
На обложке тетради должны быть ясно написаны: фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы, номер варианта, название дисциплины; здесь же следует указать дату отсылки работы в университет и домашний адрес студента (в соответствии с образцом оформления титульного листа). Выполненные задания должны завершаться списком используемой литературы, проставленной датой её выполнения и подписью.
В работу должны быть включены решения всех задач, соответствующих варианту. Контрольные работы, не содержащие решения всех задач, а также содержащие решения задач не своего варианта, не зачитываются.
Решения задач надо располагать в порядке нумерации, указанной в задании.
Перед решением каждой задачи надо выписать полностью ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, соответствующими своему варианту.
Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя основные действия по ходу решения и делая необходимые чертежи.
При получении прорецензированной работы, как незачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все его рекомендации.
Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в кратчайшее время.
На повторную проверку обязательно представляется также и ранее прорецензированная работа с рецензией на нее. Вносить исправления в сам текст работы после рецензирования недопустимо.
ЗАДАНИЕ 1. Дана система линейных уравнений:
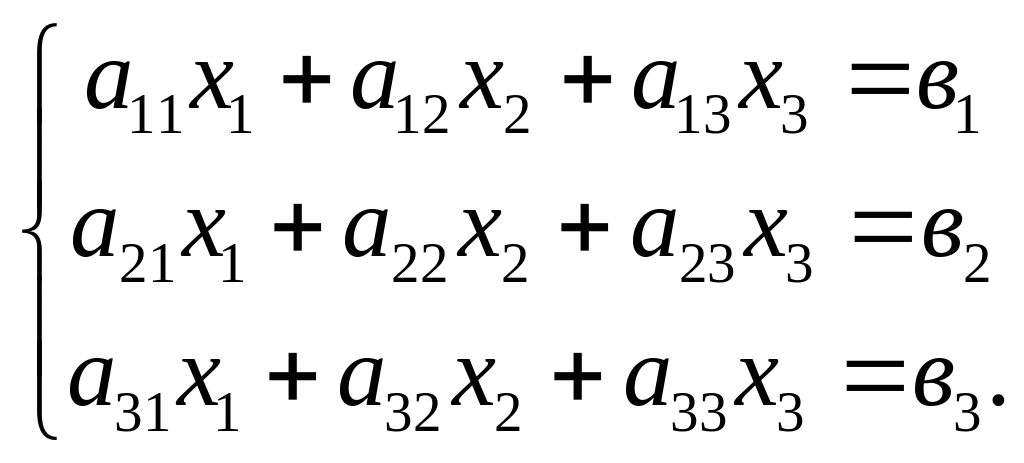
Доказать совместность этой системы и решить ее двумя способами:
1) по формулам Крамера;
2) матричным методом (с помощью обратной матрицы) и проверить
выполнение
условия
![]() .
.
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
|
ЗАДАНИЕ
2. В пространстве заданы четыре точки
своими координатами
![]()
![]()
![]() и
и
![]()
Необходимо найти:
косинус угла
 (cos
(cos
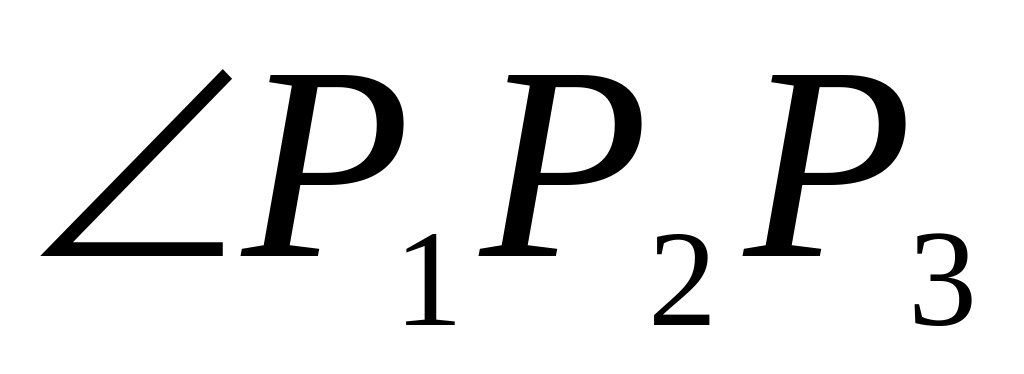 )
с помощью скалярного произведения
векторов;
)
с помощью скалярного произведения
векторов;площадь треугольника (
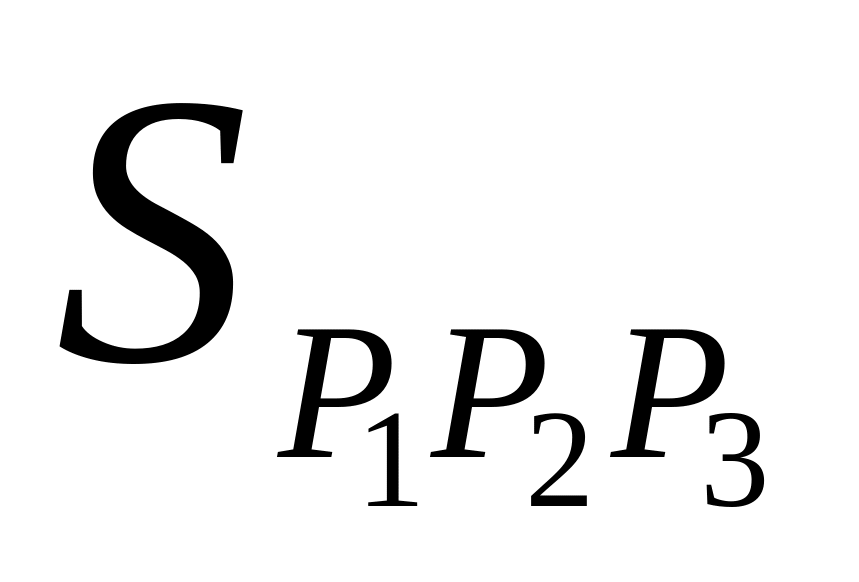 )
с помощью векторного произведения
векторов;
)
с помощью векторного произведения
векторов;объем V пирамиды
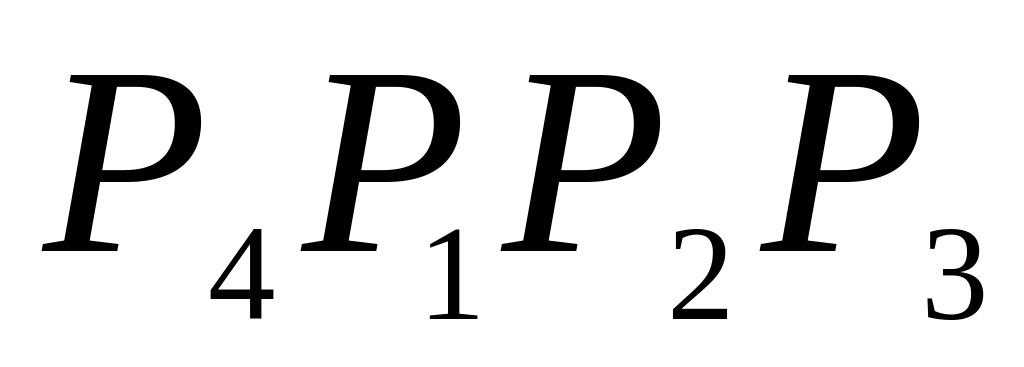 с помощью смешанного произведения
векторов;
с помощью смешанного произведения
векторов;координаты проекции точки
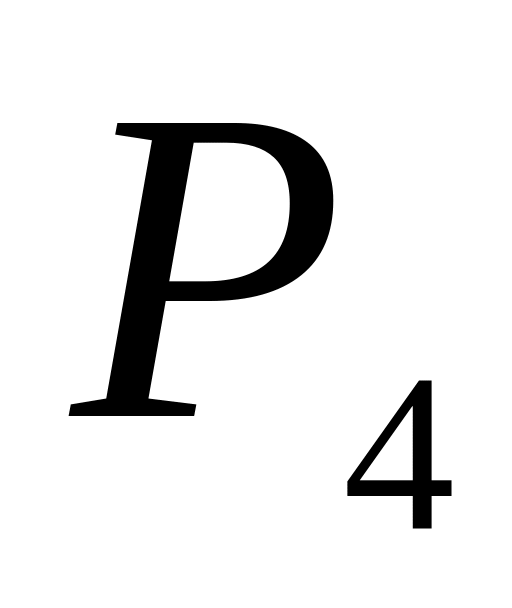
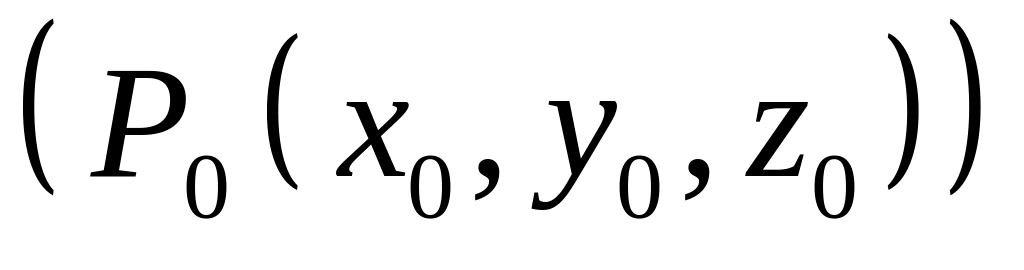 на плоскость основания
на плоскость основания
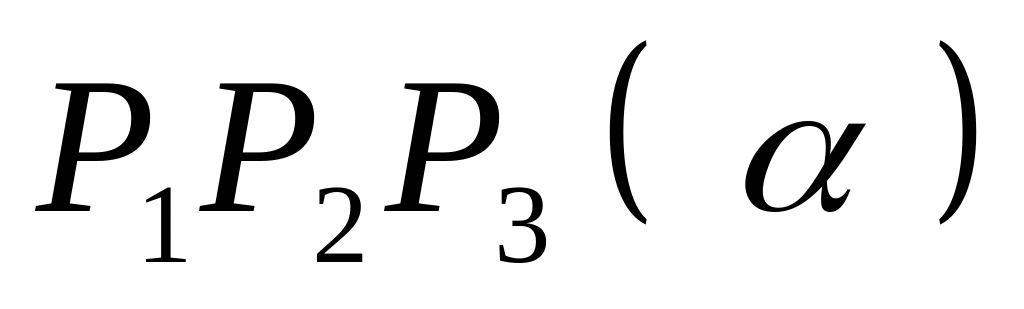 .
.
N варианта |
|
|
|
|
1 |
(0; 1; 0) |
(1; 0; 1) |
(2; 1; 4) |
(3; 0; -1) |
2 |
(0; 1; 4) |
(1; 0; 5) |
(2; 1; 8) |
(-7; -3; 4) |
3 |
(1; -1; 0) |
(1; 2; 3) |
(2; 1; 4) |
(-5; -4; 3) |
4 |
(-1; 2; 3) |
(-2; 2; 1) |
(1; -1; 4) |
(5; 3; -2) |
5 |
(-1; 1; -2) |
(0; 2; 1) |
(-2; 2; -3) |
(7; 2; -3) |
6 |
(1; 1; 6) |
(1; 2; 7) |
(0; 2; 5) |
(-5; -2; 3) |
7 |
(-1; 2; -1) |
(0; 1; 0) |
(-2; 2; -3) |
(-3; -3; 2) |
8 |
(1; 0; 5) |
(0; 2; 5) |
(1; -1; 4) |
(3; 2; -1) |
9 |
(2; 1; 4) |
(0; 2; 1) |
(1; 2; 3) |
(5; 1; -2) |
10 |
(-1; 2; 3) |
(0; 1; 4) |
(-1; 1; 2) |
(-3; -1; 2) |
11 |
(0; 2; 1) |
(1; 1; 2) |
(1; -1; 0) |
(-1; -2; 1) |
12 |
(2; 1; 8) |
(-2; 2; 1) |
(1; 1; 6) |
(1; 1; 0) |
13 |
(-1; 1; -2) |
(-2; 2; -3) |
(-1; 2; -1) |
(5; 1; -2) |
14 |
(1; 2; 7) |
(-1; 1; 2) |
(0; 1; 4) |
(-5; -2; 3) |
15 |
(1; 0; 1) |
(1; 2; 3) |
(0; 2; 1) |
(-5; -4; 3) |
16 |
(1; 0; 5) |
(2; 1; 8) |
(1; 1; 6) |
(3; 2; -1) |
17 |
(0; 1; 0) |
(1; 1; 2) |
(-2; 2; -3) |
(-3; -3; 2) |
18 |
(-1; 1; 2) |
(1; -1; 4) |
(0; 2; 5) |
(5; 3; -2) |
19 |
(1; 0; 1) |
(2; 1; 4) |
(0; 2; 1) |
(7; 2; -3) |
20 |
(-2; 2; 1) |
(1; 2; 7) |
(1; -1; 4) |
(-3; -1; 2) |
21 |
(1; 1; 2) |
(-1; 2; -1) |
(1; 2; 3) |
(3; 0; -1) |
22 |
(2; 1; 8) |
(0; 1; 4) |
(1; 2; 7) |
(1; 1; 0) |
23 |
(-1; 1; -2) |
(-2; 2; -3) |
(2; 1; 4) |
(-1; -2; 1) |
24 |
(-1; 2; 3) |
(1; 0; 5) |
(-2; 2; 1) |
(-7; -3; 4) |
25 |
(0; 1; 0) |
(-1; 2; -1) |
(0; 2; 1) |
(-1; -2; 1) |
ЗАДАНИЕ 3. Вычислить пределы. В заданиях а), б), в) – непосредственно, г) с помощью замены эквивалентными бесконечно малыми, д) применяя правило Лопиталя.
а)
![]()
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
|
|
б)
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
|
|
в)![]()
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
|
|
г)
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
|
|
д)
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
|
|
ЗАДАНИЕ
4. Исследовать
на непрерывность функцию
![]() и
построить схематический график.
и
построить схематический график.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
|
|
ЗАДАНИЕ
5. Методами
дифференциального исчисления исследовать
функцию
![]() и построить ее график.
и построить ее график.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
|
|
ЗАДАНИЕ
6. Найти
полный дифференциал
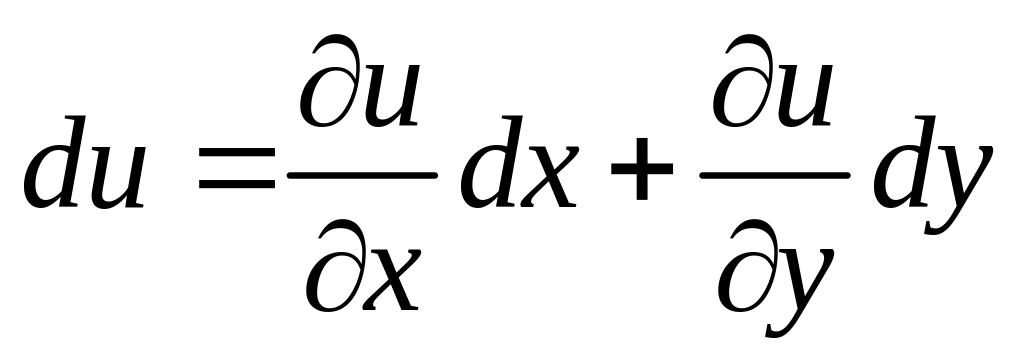 функции
функции
![]()
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
|
|
Образец выполнения контрольной работы
Пример 1. Дана система линейных уравнений
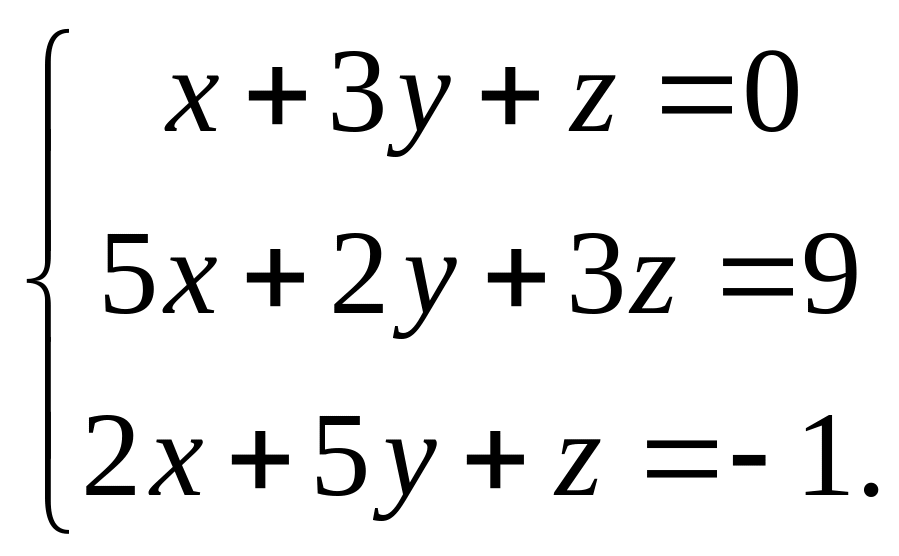
Доказать совместность этой системы и решить ее двумя способами:
1) по формулам Крамера;
2) матричным методом (с помощью обратной матрицы) и проверить
выполнение условия .
Решение
Совместность данной системы докажем, используя теорему Крамера, а именно: если главный определитель системы отличен от нуля, то система имеет единственное решение.
Вычислим главный определитель системы, пользуясь правилом треугольников:
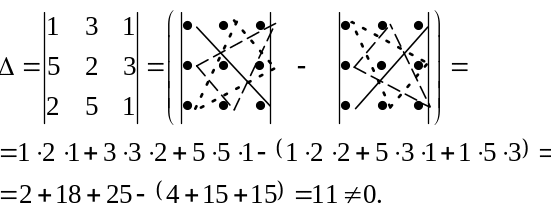
Так как главный определитель системы отличен от нуля, то система совместна и имеет единственное решение.
Решим систему уравнений по формулам Крамера:
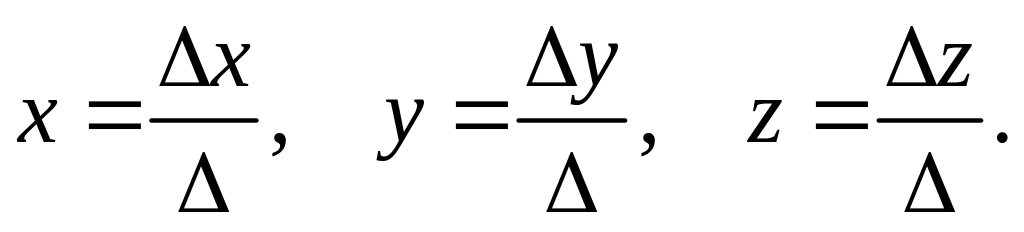
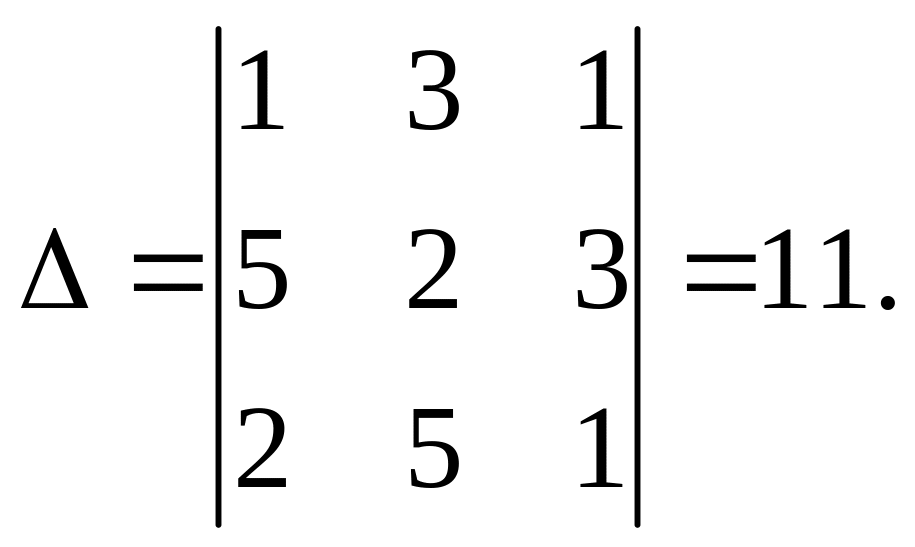
Вычислим
вспомогательные определители
![]() , для чего у главного определителя
заменим соответствующий столбец столбцом
свободных членов:
, для чего у главного определителя
заменим соответствующий столбец столбцом
свободных членов:
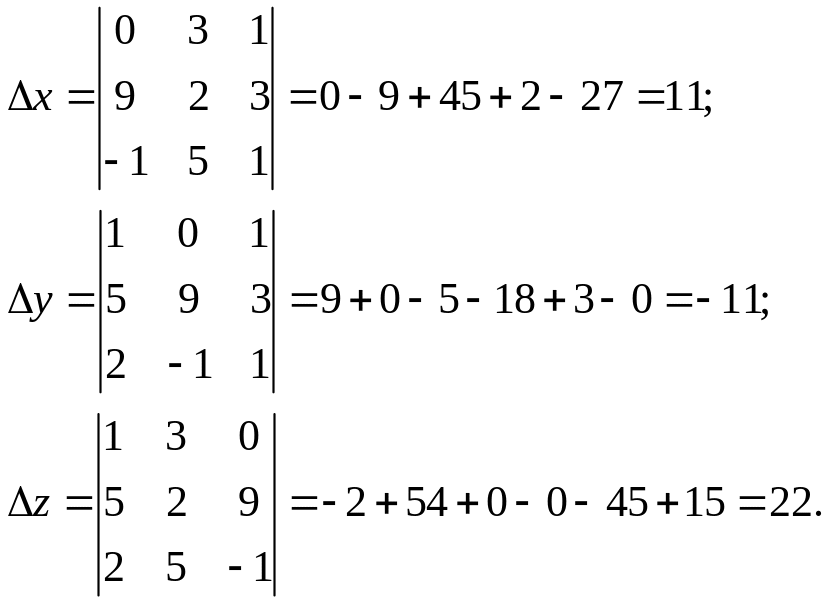
По формулам Крамера получаем:
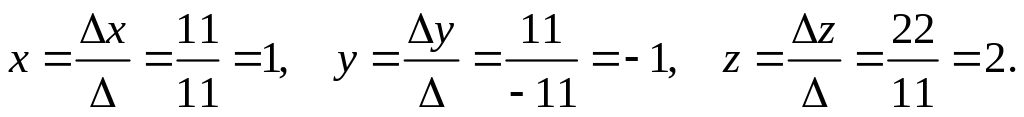
Ответ:
![]()
Замечание: Определитель также удобно вычислять путем разложения по элементам первой стоки по формуле:
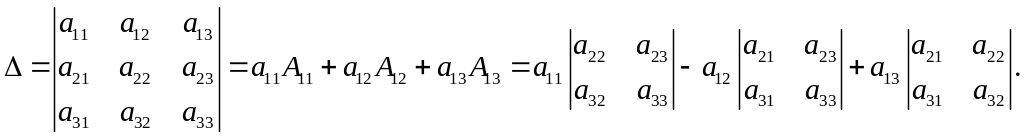
Решим систему линейных уравнений матричным методом.
Обозначим
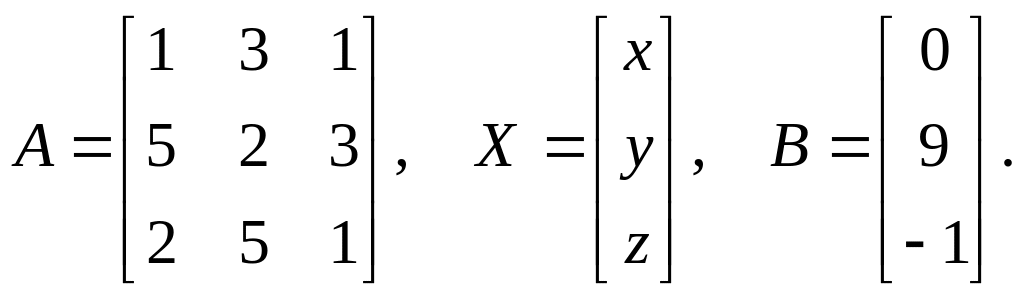
Тогда
данную систему можно записать в виде:
![]() .
.
Если
матрица А
невырожденная,
то есть
![]() (
(![]() ̶ определитель матрицы А),
то
̶ определитель матрицы А),
то
![]() где
где
![]() ̶ матрица, обратная матрице А.
Обратная матрица
определяется по формуле
̶ матрица, обратная матрице А.
Обратная матрица
определяется по формуле
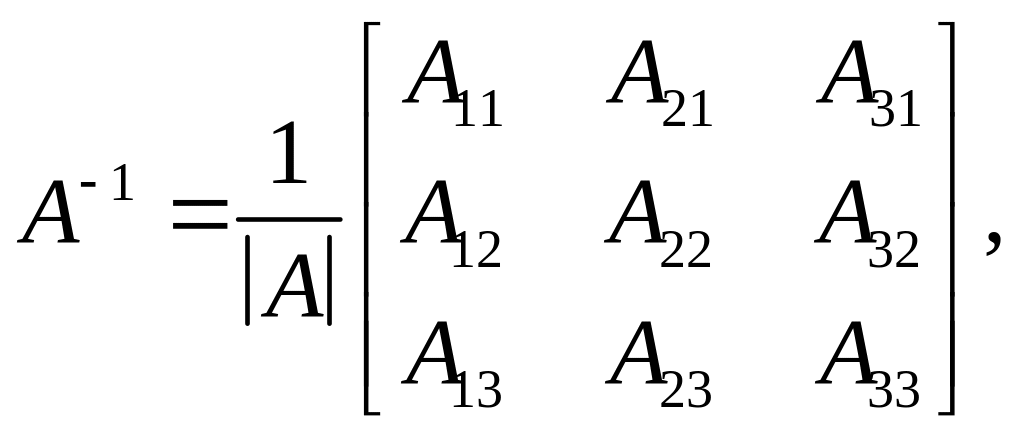
где
![]() ̶ алгебраические дополнения элементов
̶ алгебраические дополнения элементов
![]() в определителе
в определителе
![]() (
(![]() ̶ миноры, соответствующие элементам
̶ миноры, соответствующие элементам
![]() определителя
,
которые являются определителями второго
порядка, получаемые из определителя
путем вычеркивания строки i
и
столбца
j).
определителя
,
которые являются определителями второго
порядка, получаемые из определителя
путем вычеркивания строки i
и
столбца
j).
Для
нашего случая имеем
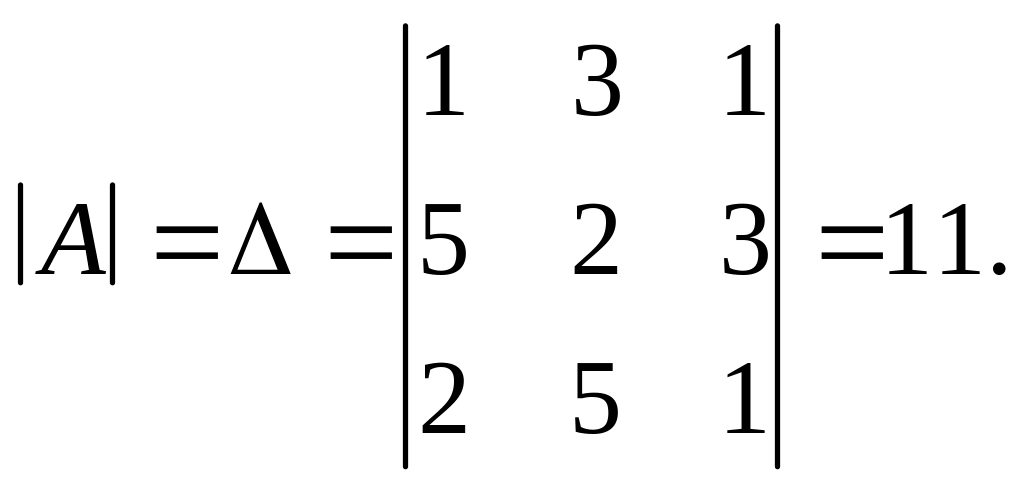
Так как , то существует обратная матрица .
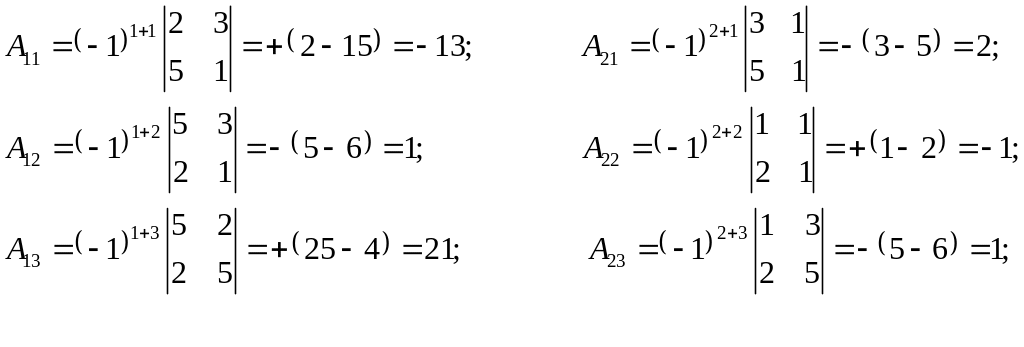
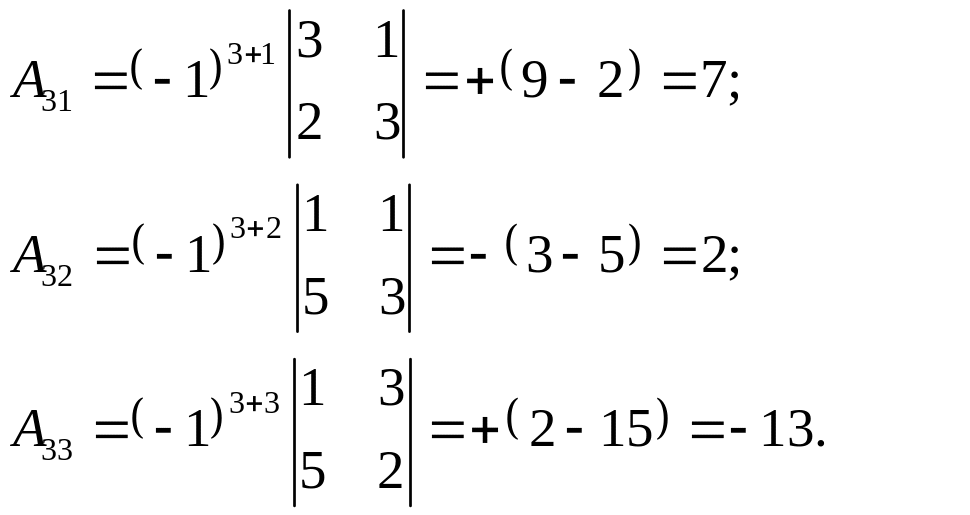
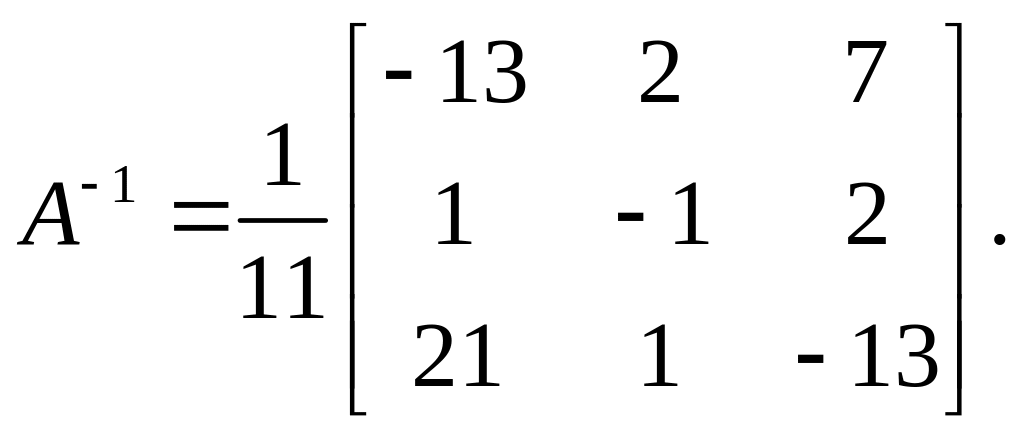
Итак,
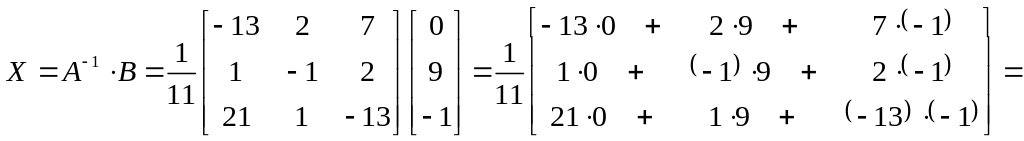
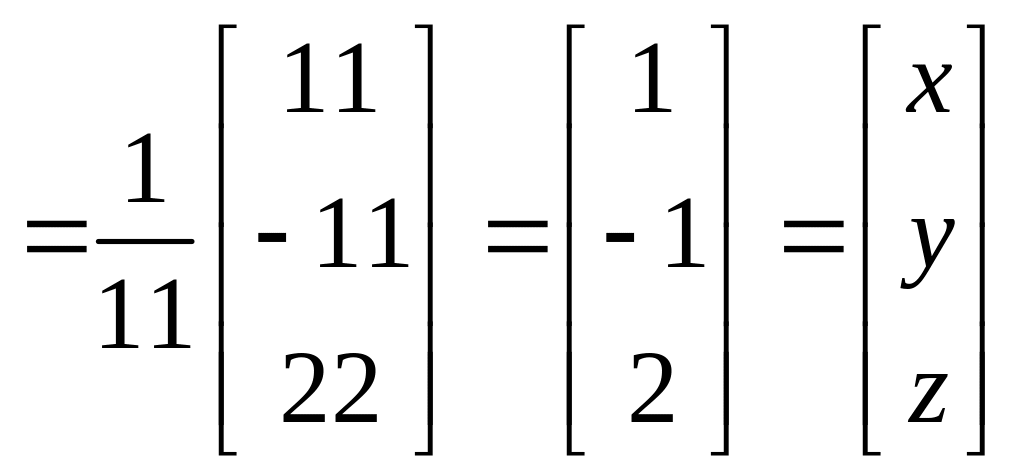 .
.
Проверим
выполнение условия
![]()

Ответ:
Пример
2.
В пространстве заданы четыре точки
своими координатами
![]()
![]()
![]() и
и
![]()
Необходимо найти:
косинус угла (cos ) с помощью скалярного произведения векторов;
площадь треугольника (
 )
с помощью векторного произведения
векторов;
)
с помощью векторного произведения
векторов;объем V пирамиды с помощью смешанного произведения векторов;
координаты проекции вершины
 на плоскость основания
на плоскость основания
 .
.
Решение
Известно, что косинус угла
 между векторами
между векторами
 и
и
![]() определяется
по формуле
определяется
по формуле
 где скалярное произведение векторов
и
определяется по формуле
где скалярное произведение векторов
и
определяется по формуле
![]() ,
а длины векторов
,
а длины векторов
![]() и
и
![]() равны
равны
![]() и
и
![]()
Угол
̶ это угол между векторами
![]() и
и![]() .
Найдем координаты этих векторов,
используя формулу
.
Найдем координаты этих векторов,
используя формулу
![]() ,
где
,
где
![]() и
и
![]() .
.
![]()
![]()
Следовательно,
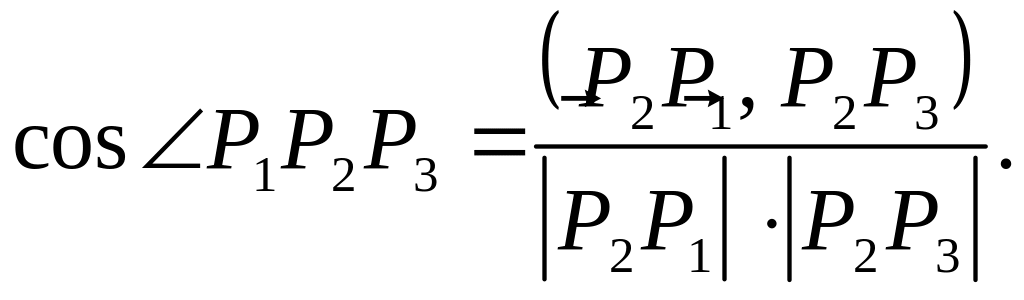
![]()
![]()
![]()
Итак
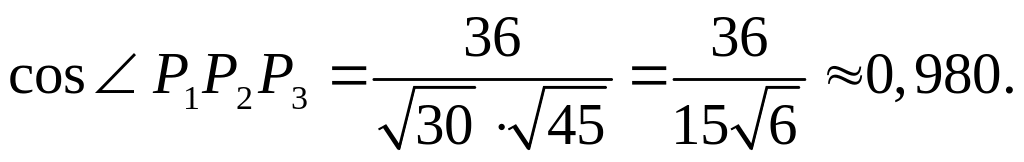
Известно, что площадь S треугольника, построенного на векторах
 и
и
 как на сторонах, вычисляется по формуле
как на сторонах, вычисляется по формуле
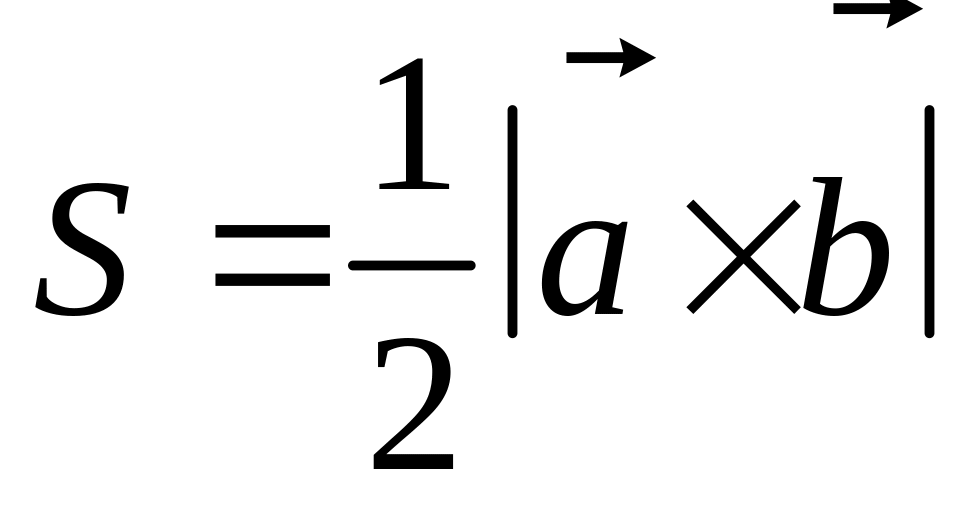 ,
где
,
где
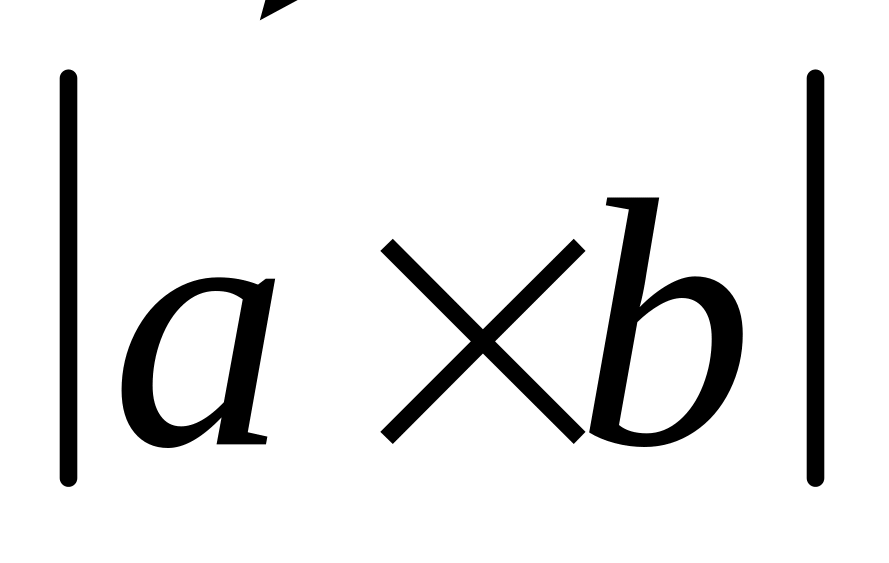 ̶ модуль векторного произведения
векторов
и
.
Векторное произведение векторов
и
вычисляем по формуле
̶ модуль векторного произведения
векторов
и
.
Векторное произведение векторов
и
вычисляем по формуле
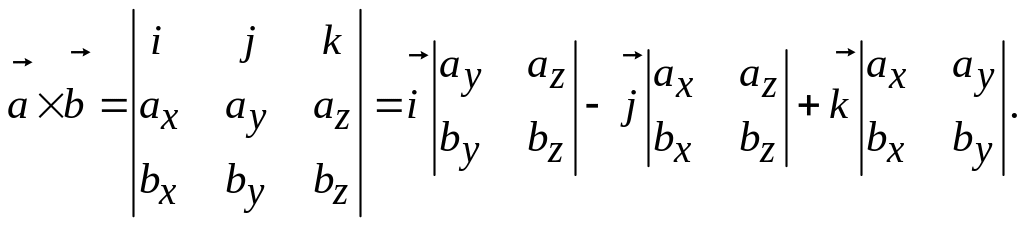
Для нашего случая имеем
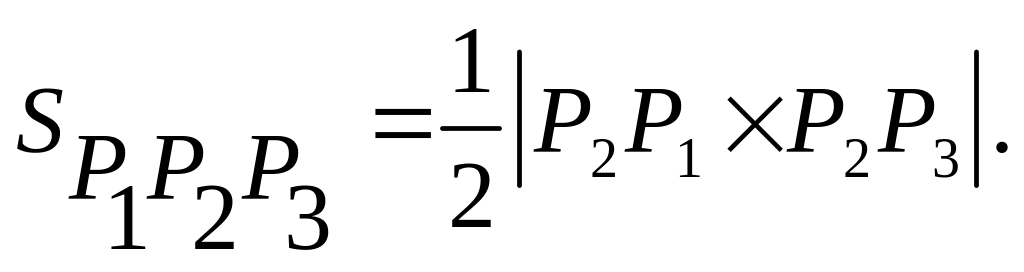
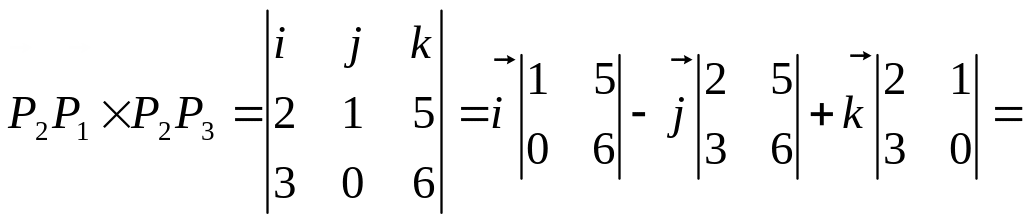
![]()
![]()
Тогда
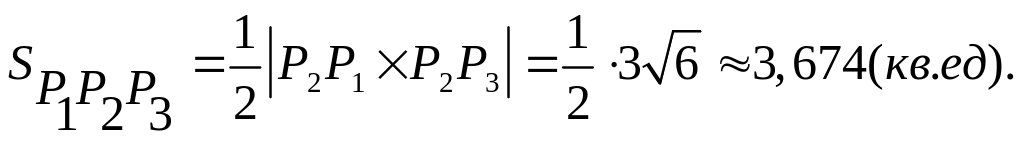
Пирамиду можно рассматривать как пирамиду, построенную на векторах , и
 .
Тогда
.
Тогда
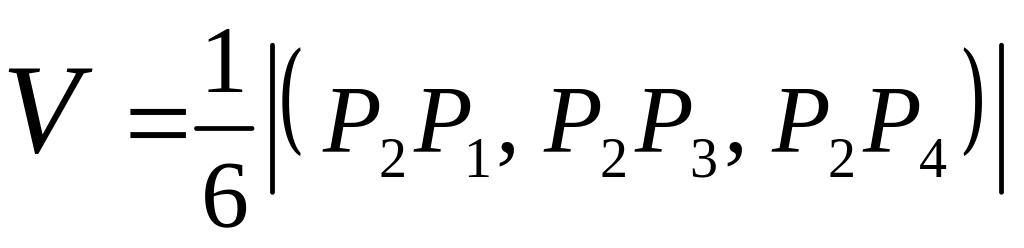 ,
где
,
где
![]() ̶ смешанное
произведение векторов, определяемое
по формуле
̶ смешанное
произведение векторов, определяемое
по формуле
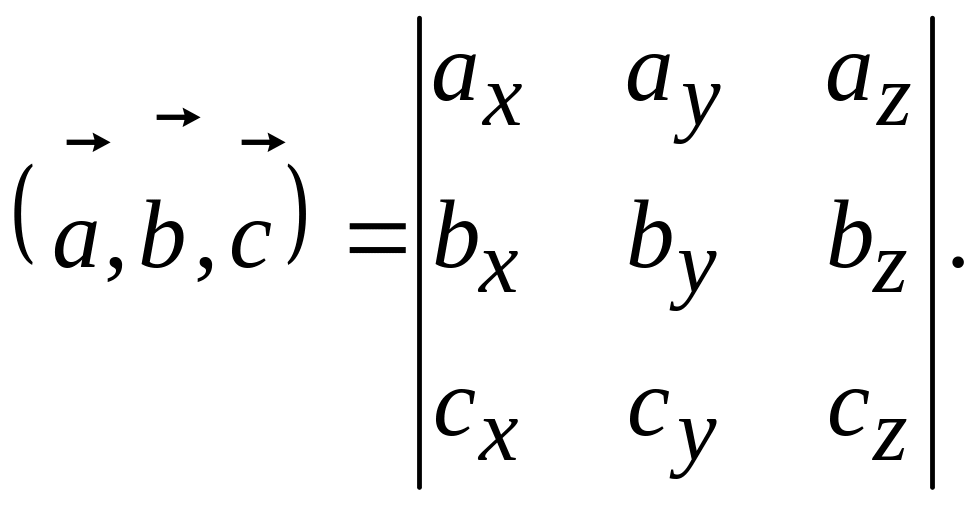
Найдем
координаты вектора
![]()
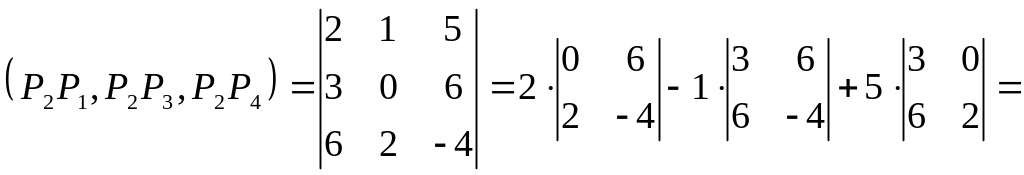
![]()

Найти координаты проекции вершины
 на
плоскость основания
на
плоскость основания
 , это значит надо найти координаты точки
пересечения прямой l,
проходящей через вершину
перпендикулярно плоскости основания
(т.е. плоскости
,
проходящей через вершины
).
, это значит надо найти координаты точки
пересечения прямой l,
проходящей через вершину
перпендикулярно плоскости основания
(т.е. плоскости
,
проходящей через вершины
).
Сначала найдем уравнение плоскости . Воспользуемся уравнением плоскости, проходящей через три точки и :
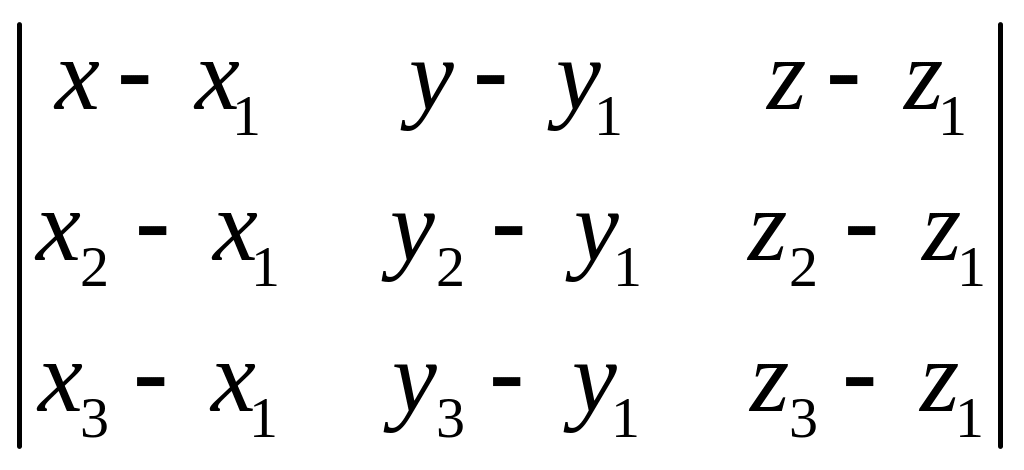 =
0.
=
0.
Для нашей задачи имеем
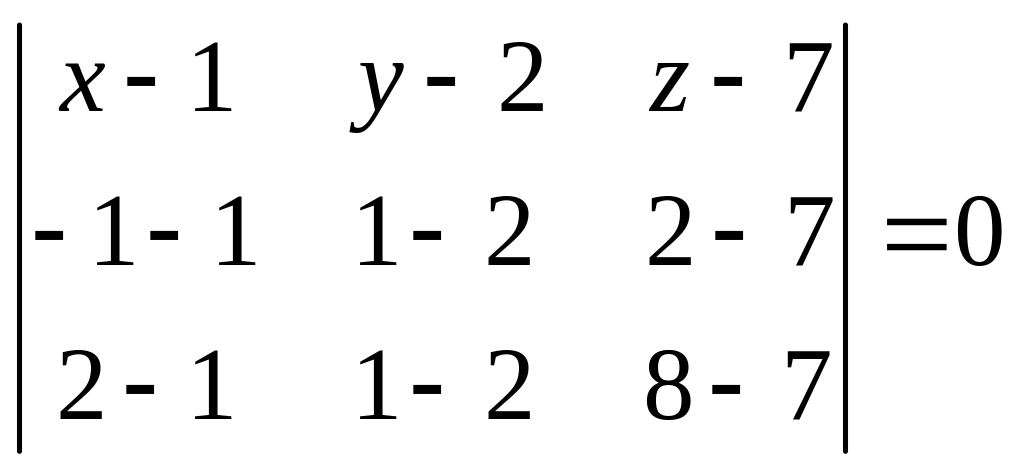 или
или
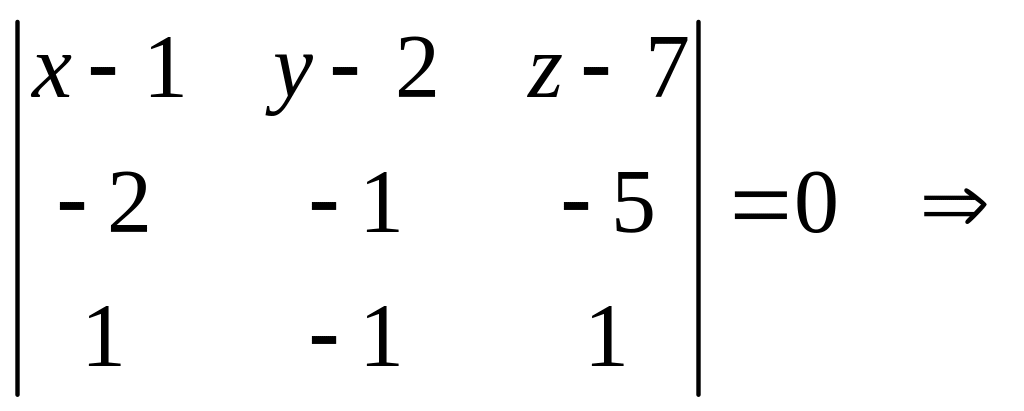
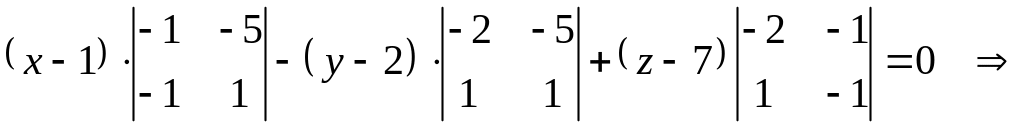
![]()
![]() уравнение
плоскости основания
уравнение
плоскости основания
![]() .
.
Найдем
канонические уравнения прямой, проходящей
через вершину
перпендикулярно плоскости основания
.Известно,
что канонические уравнения прямой,
проходящей через точку
![]() перпендикулярно плоскости
перпендикулярно плоскости
![]() , имеют вид:
, имеют вид:
 .
.
В нашем случае имеем
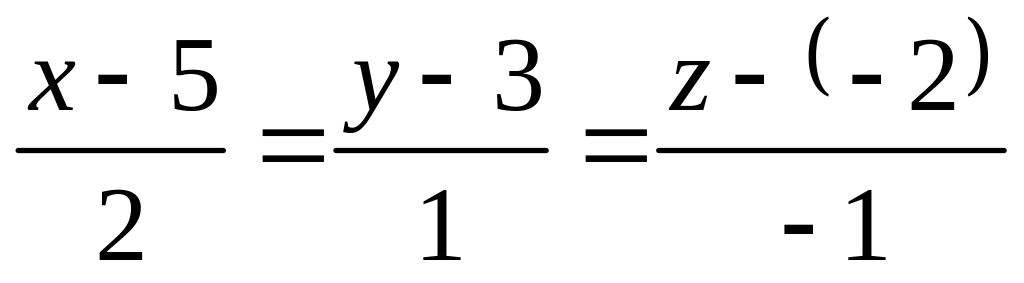 или
или
 .
.
Перейдем к параметрическим уравнениям прямой l:
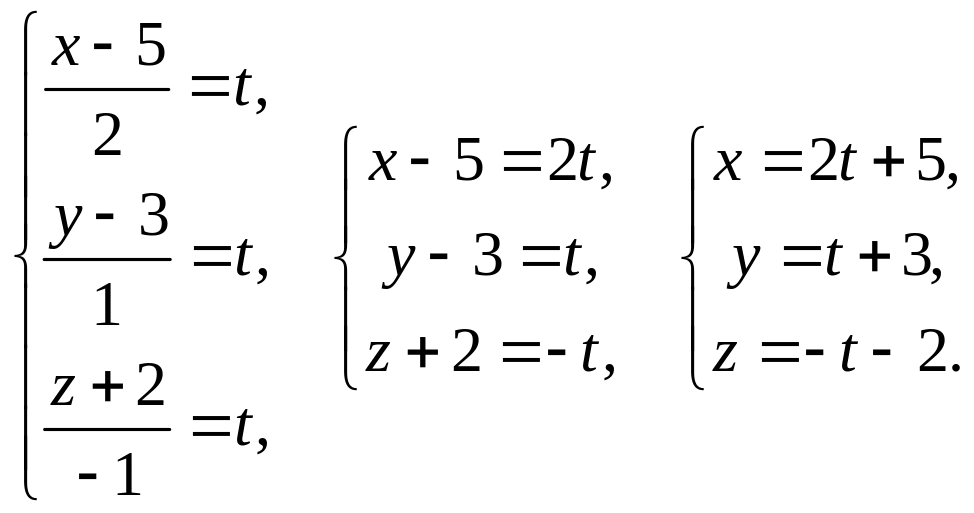
Подставим
выражения x,
y,
z
через t
в
уравнение плоскости
![]() :
:
![]()
![]()
![]()
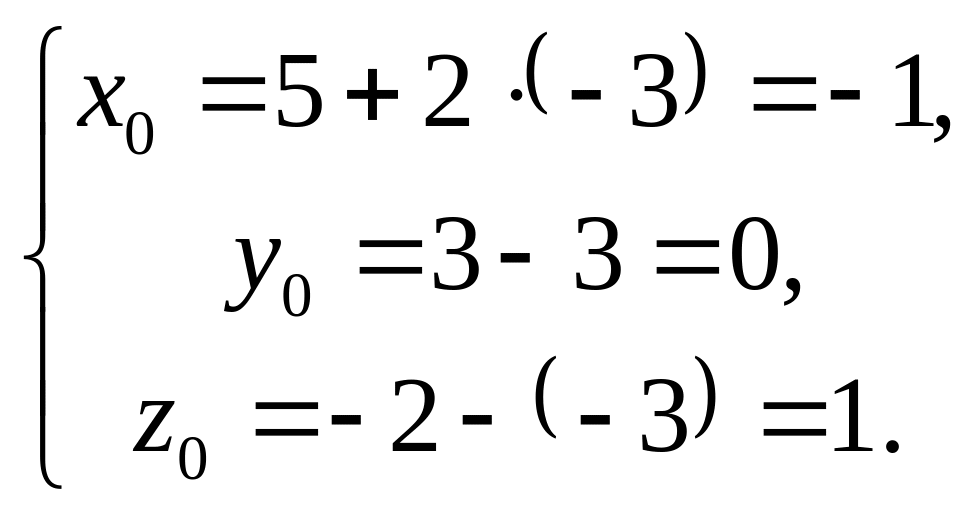
![]() .
.
Ответ:
1)
![]() 2)
2)
![]() 3)
3)![]()
4) .
Пример 3. Найти пределы. В заданиях а), б), в) – непосредственно, г) с помощью замены эквивалентными бесконечно малыми, д) применяя правило Лопиталя.
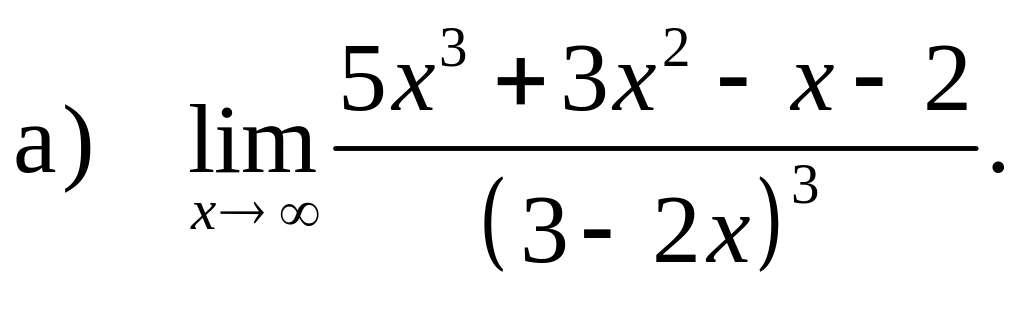
Решение
Так
как
![]() и
и
![]() ,
то имеем неопределенность вида
,
то имеем неопределенность вида
![]() .
Для раскрытия этой неопределенности
преобразуем дробь:
.
Для раскрытия этой неопределенности
преобразуем дробь:
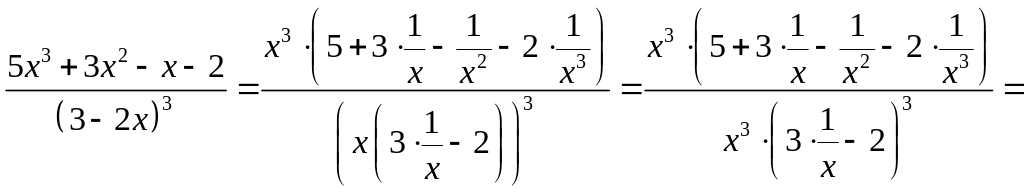
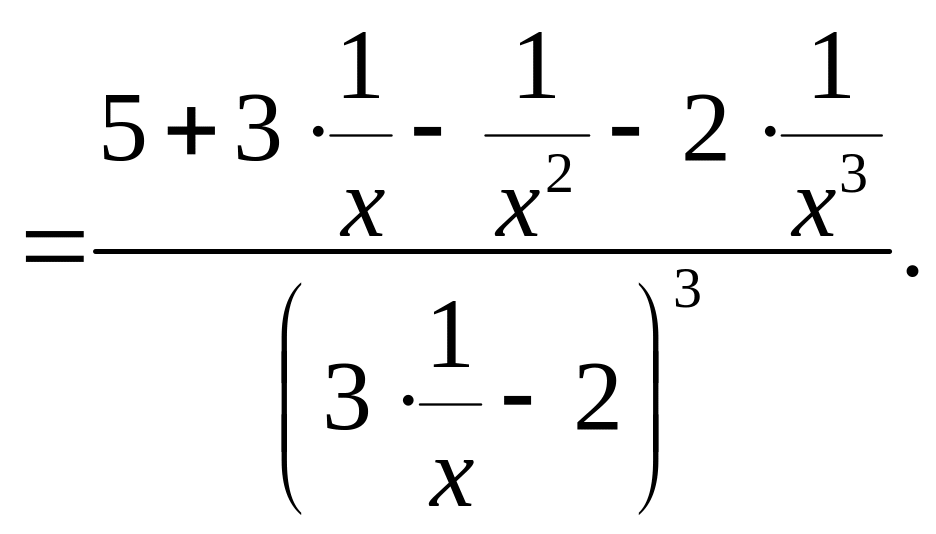
Но так как
 ,
то имеем
,
то имеем

б)
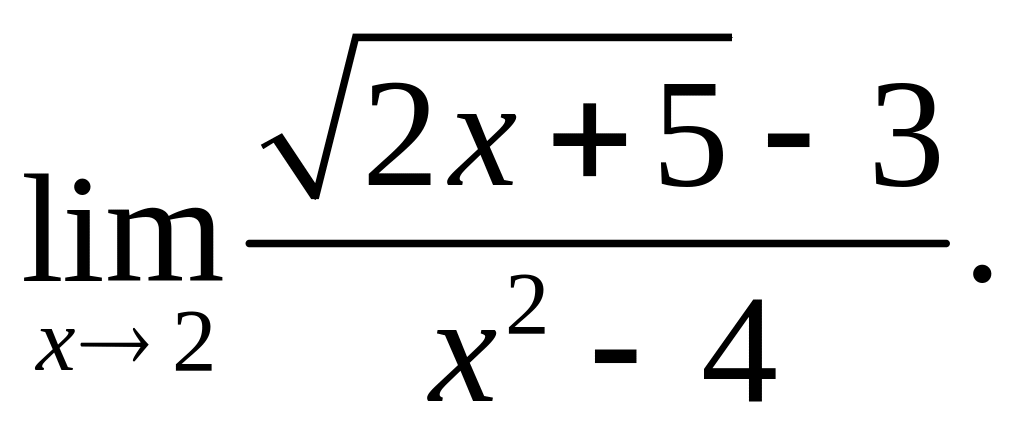
Решение
Так
как
![]() и
и
![]() ,
то имеем неопределенность вида
,
то имеем неопределенность вида
![]() ,
которую можем раскрыть, умножив числитель
и знаменатель дроби на выражение,
сопряженные числителю, т.е. на
,
которую можем раскрыть, умножив числитель
и знаменатель дроби на выражение,
сопряженные числителю, т.е. на
![]() (так как
(так как
![]()
Итак,
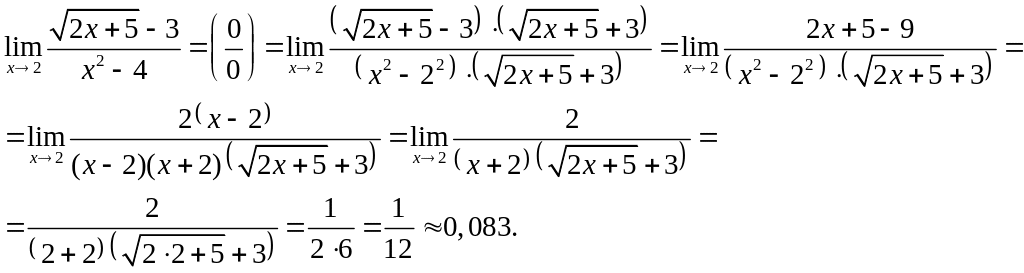 в)
в)
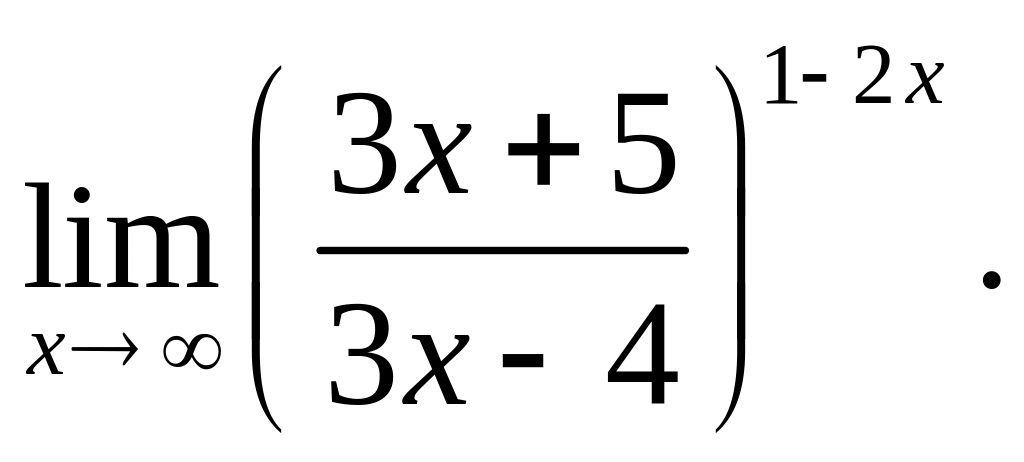
Решение
Так как
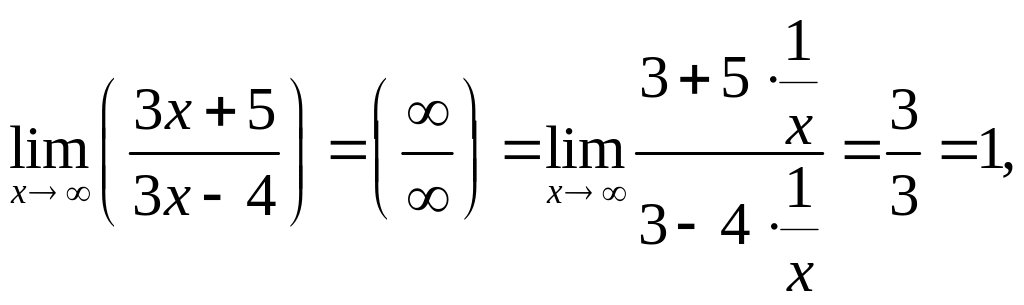
![]()
то
мы имеем неопределенность вида
![]() .
Для раскрытия этой неопределенности
надо воспользоваться вторым замечательным
пределом. Известно, что
.
Для раскрытия этой неопределенности
надо воспользоваться вторым замечательным
пределом. Известно, что
 Поэтому представим основание степени
в виде
Поэтому представим основание степени
в виде
![]() ,
а в показателе степени выделяем множитель
,
а в показателе степени выделяем множитель
![]() :
:
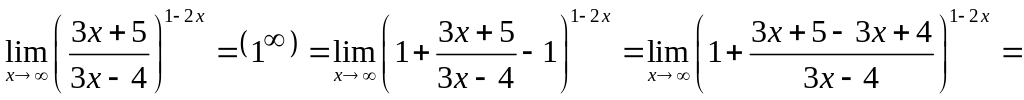
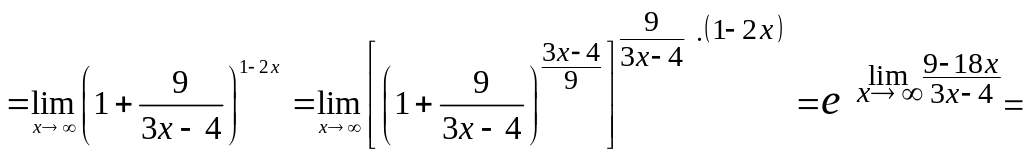
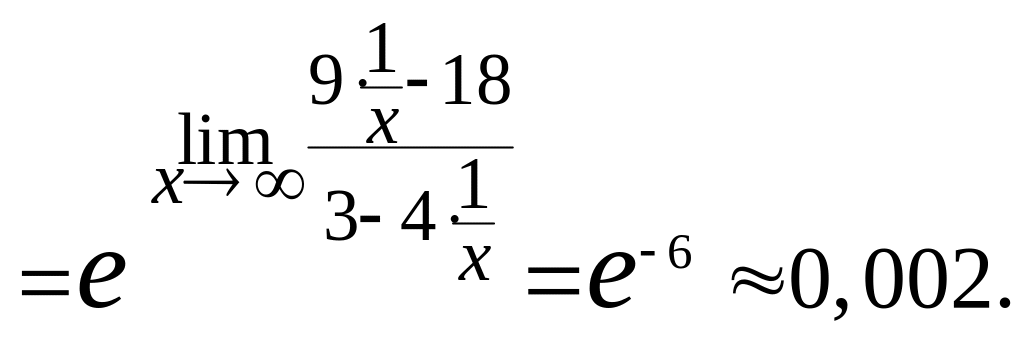
Здесь
![]() так как
так как
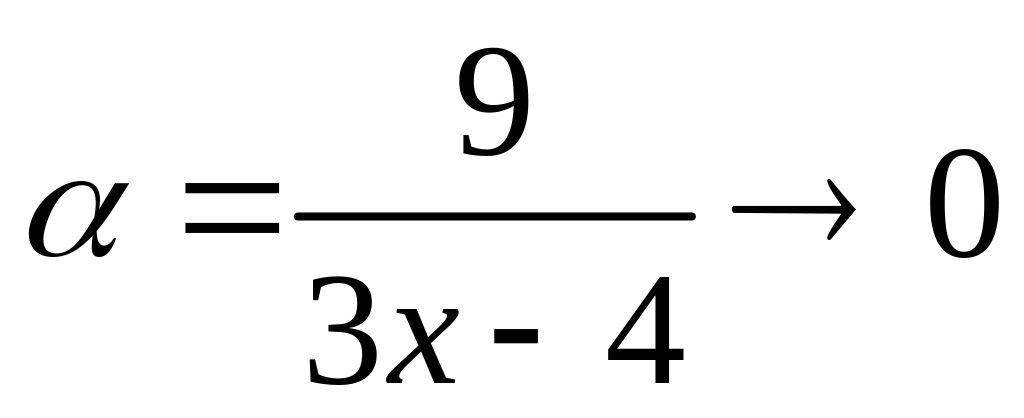 при
при
![]() ,
то
,
то
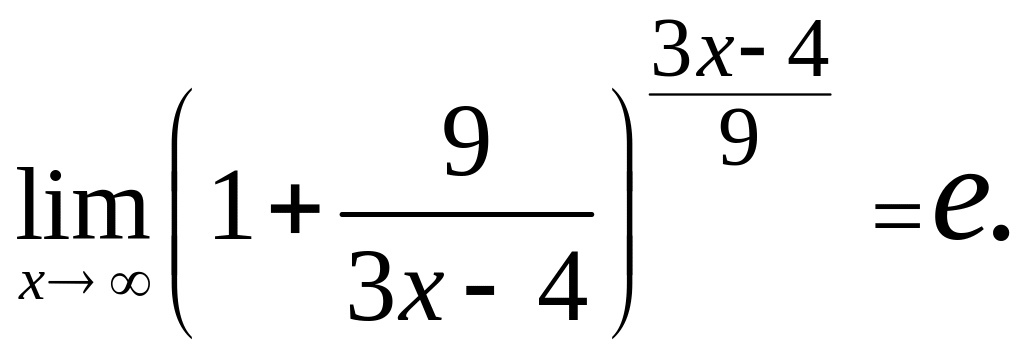
г)
 .
.
Решение
При
![]()
![]() и
и
![]() ,
а так как при нахождении предела отношения
двух бесконечно малых каждую из них или
только одну можно заменить эквивалентными,
то имеем
,
а так как при нахождении предела отношения
двух бесконечно малых каждую из них или
только одну можно заменить эквивалентными,
то имеем
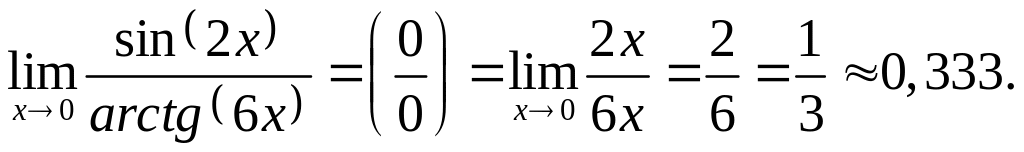
д)
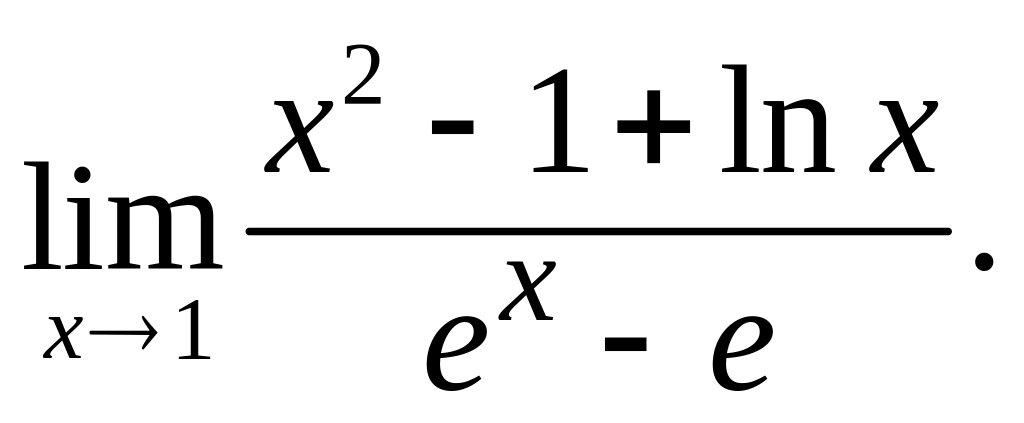
Решение
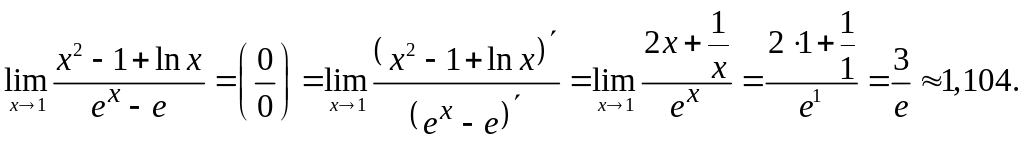
Ответ:
a)![]() б)
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
д)
;
д)![]() .
.
Пример 4. Исследовать на непрерывность функцию
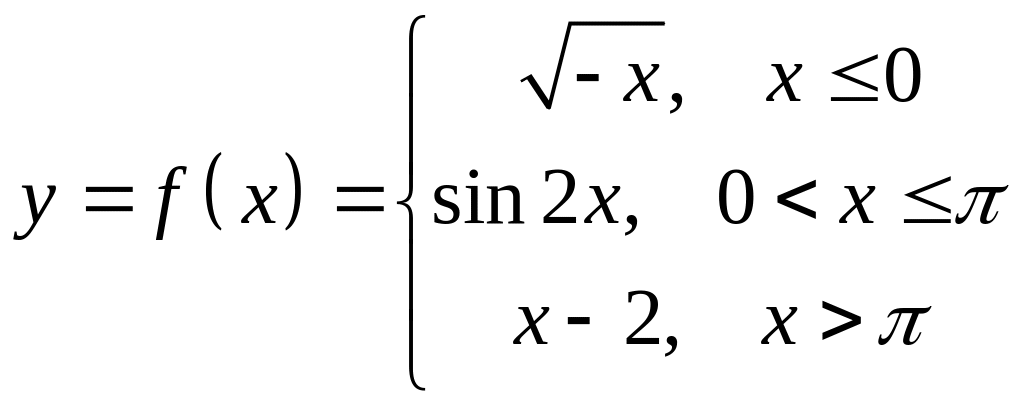 и
построить схематический график.
и
построить схематический график.
Решение
Данная
функция определена для всех значений
![]() и на каждом из участков задания
и на каждом из участков задания
![]() ,
,
![]() и
и
![]() является элементарной и, следовательно,
непрерывной. Непрерывность функции
может нарушиться лишь в точках, где
изменяется её аналитическое задание,
то есть в точках
является элементарной и, следовательно,
непрерывной. Непрерывность функции
может нарушиться лишь в точках, где
изменяется её аналитическое задание,
то есть в точках
![]() и
и
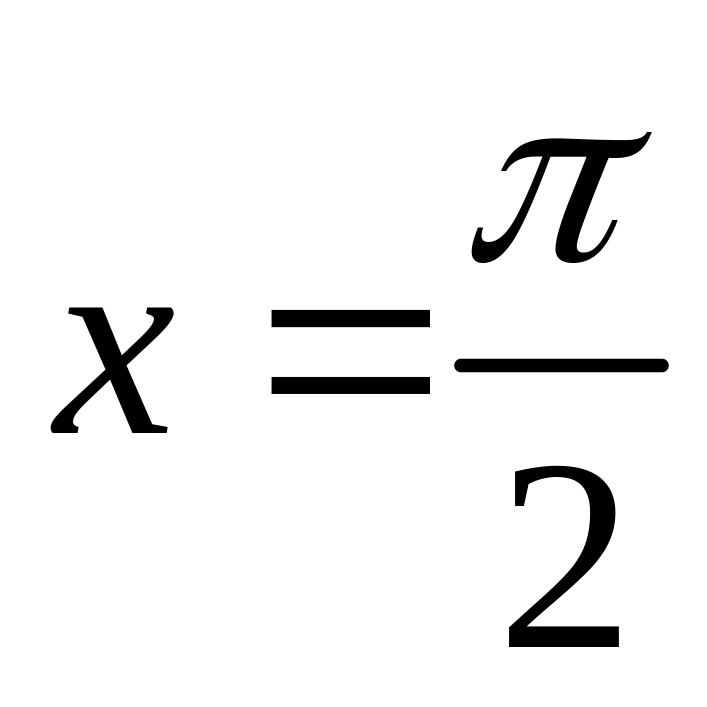 .
Исследуем эти точки на непрерывность,
находя односторонние пределы:
.
Исследуем эти точки на непрерывность,
находя односторонние пределы:
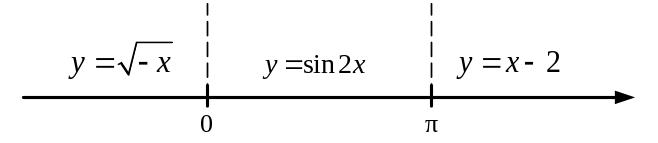
.
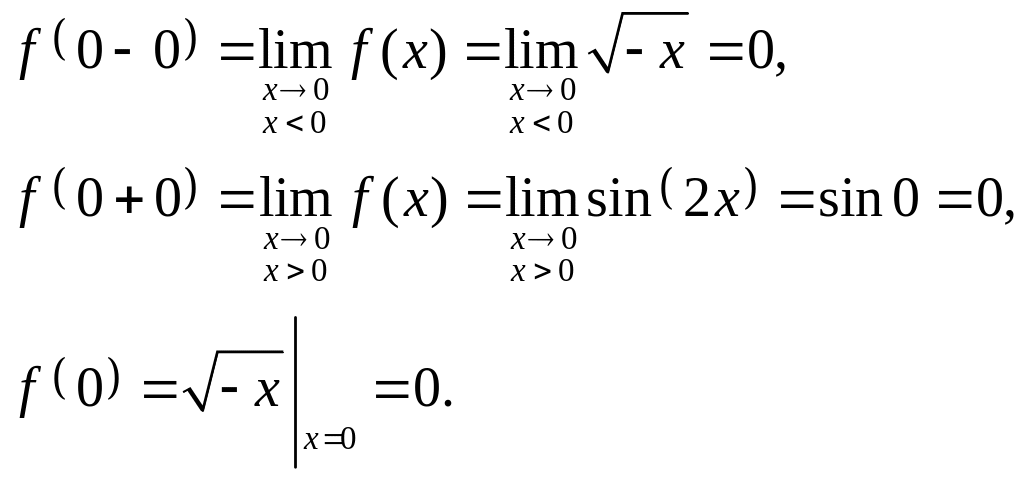
Так
как
![]() ,
то
является точкой непрерывности функции.
,
то
является точкой непрерывности функции.
![]() .
.
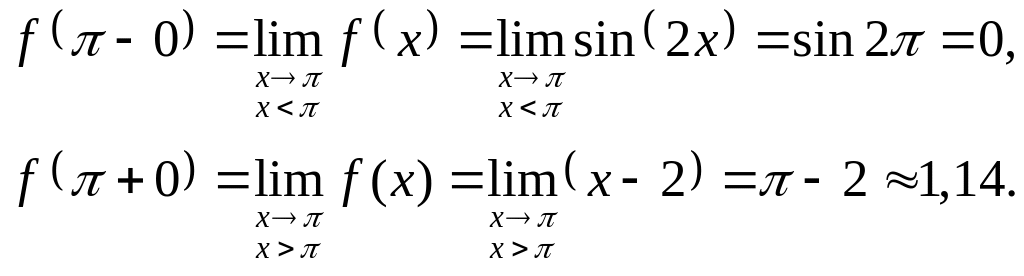
Так как в точке односторонние пределы ̶ конечные числа, но не равны между собой, то ̶ точка разрыва 1-го рода (скачок). Построим схематический график (рисунок 1).
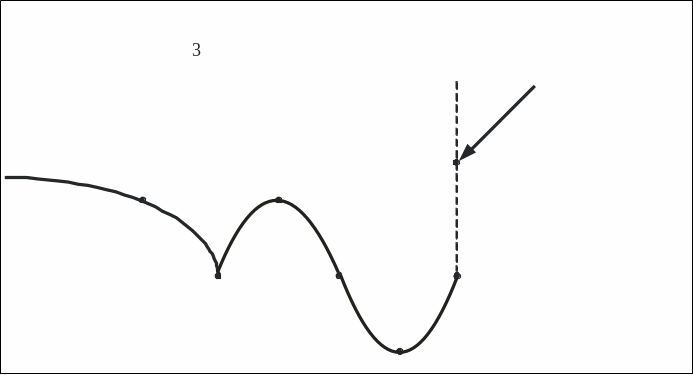
Рисунок 1 – График функции
Пример
5.
Методами дифференциального исчисления
исследовать функцию
![]() и
построить ее график.
и
построить ее график.
Решение
Исследование функции будем проводить согласно следующей схеме:
Область определения функции
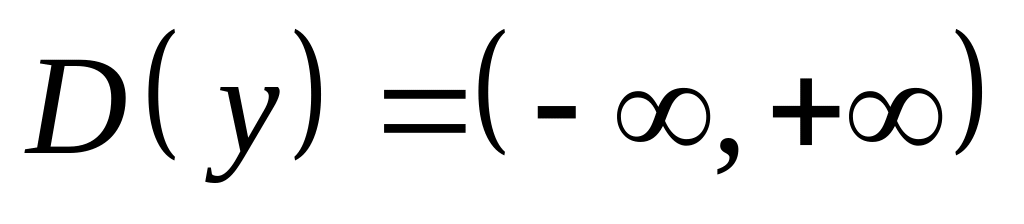 .
.Четность функции, периодичность.
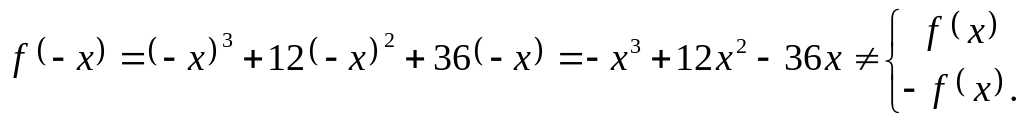
Функция не является ни четной, ни нечетной. Функция не является периодической.
Поведение функции на концах области определения.
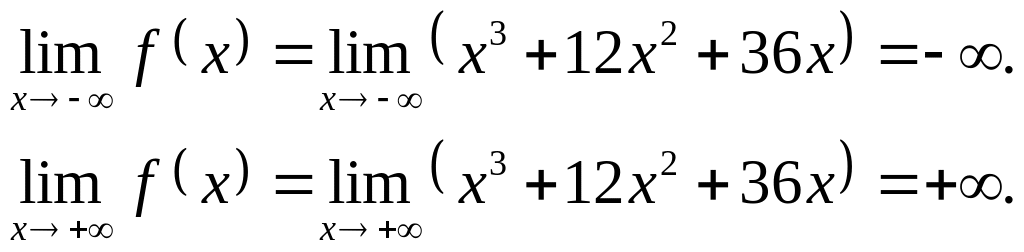
Точки пересечения с осями координат.
a)![]()
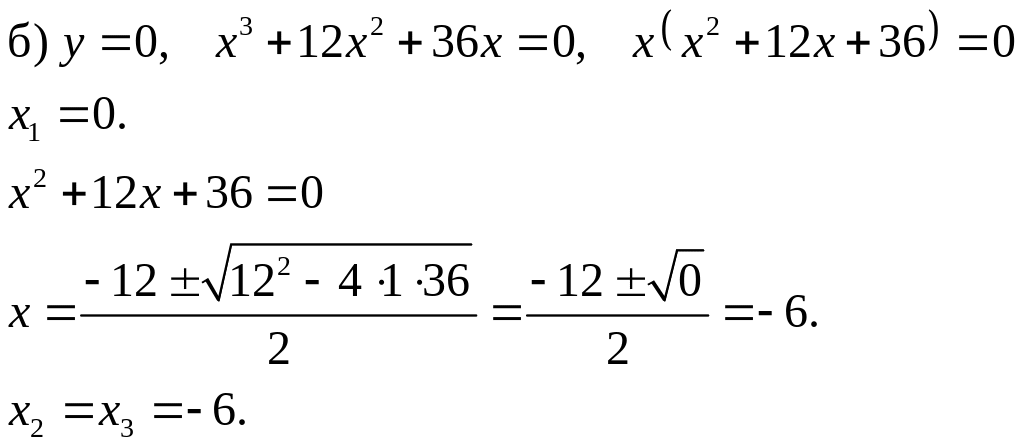
Итак, график функции пересекает оси координат в точках 0 (0,0), A (-6,0).
Исследование асимптот графика функции.
Вертикальных
асимптот нет, так как функция определена
для всех значений аргумента. Для наклонных
асимптот
![]() найдем k.
найдем k.
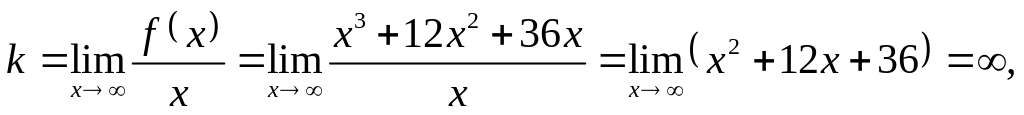 следовательно,
и наклонных асимптот нет.
следовательно,
и наклонных асимптот нет.
Исследования с помощью первой производной.
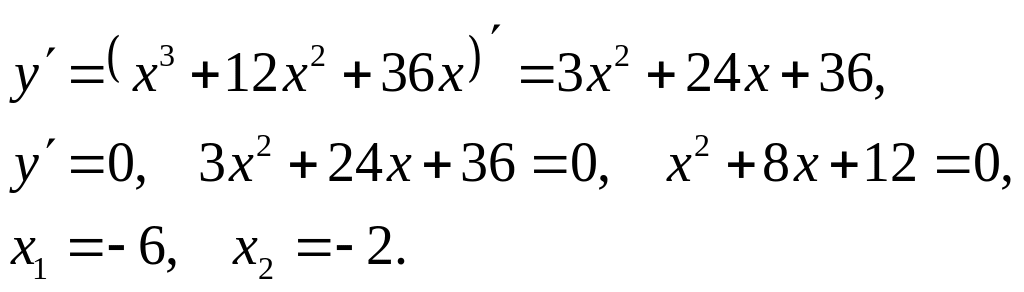
Для исследования с помощью первой производной составим таблицу 1:
Таблица 1
х |
|
-6 |
|
-2 |
|
y' |
+ |
0 |
- |
0 |
+ |
y |
|
0 |
|
-32 |
|
|
возрастает |
max |
убывает |
min |
возрастает |
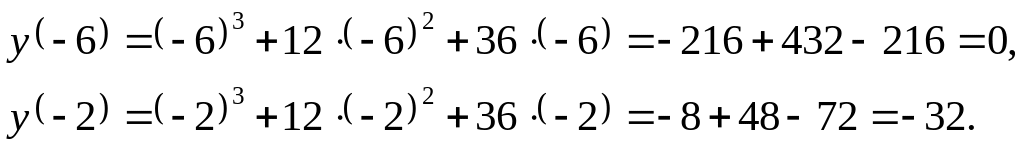
Исследования с помощью второй производной.
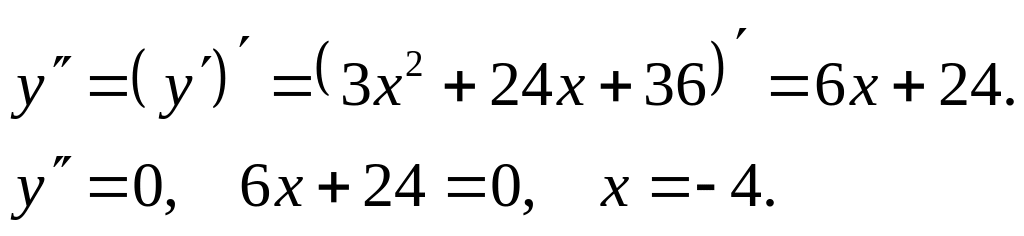
Таблица 2
х |
|
-4 |
|
y" |
- |
0 |
+ |
y |
|
-16 |
|
|
выпуклая |
точка перегиба |
вогнутая |
![]()
По результатам исследования строим график функции.

Рисунок 2 – График функции
Пример
6.
Найти полный дифференциал
функции
![]() .
.
Решение
Частные производные функции нескольких переменных определяются как производные этой функции по одному из них при условии, что остальные переменные считаются постоянными.
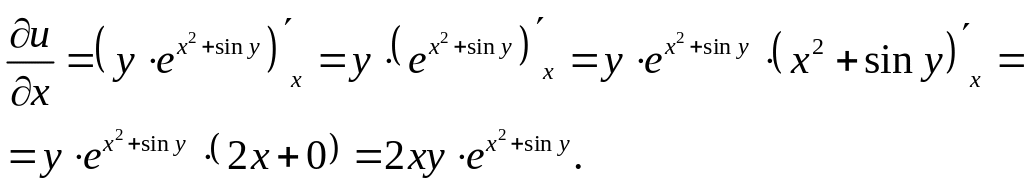
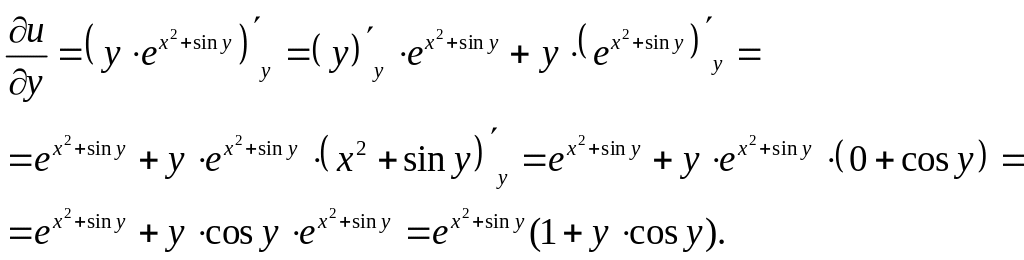
Здесь
учитывается, что
![]()
Следовательно,
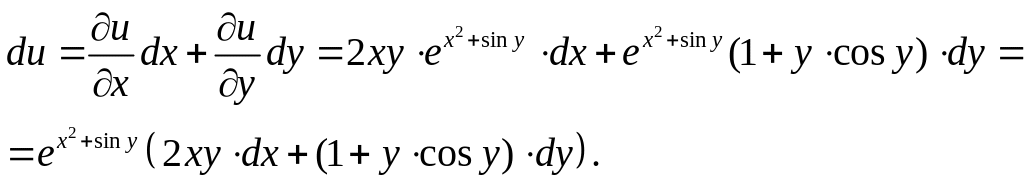
Вопросы для подготовки к экзамену

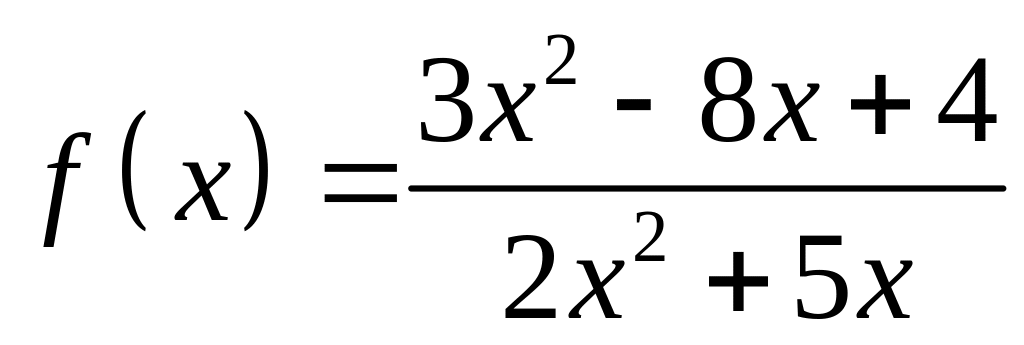
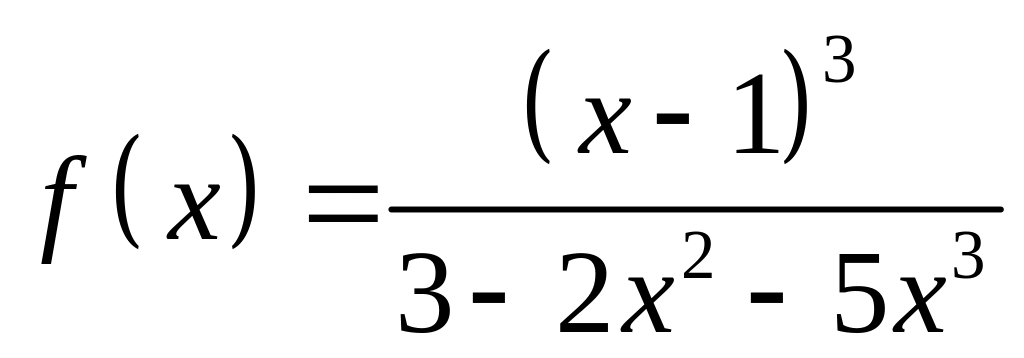
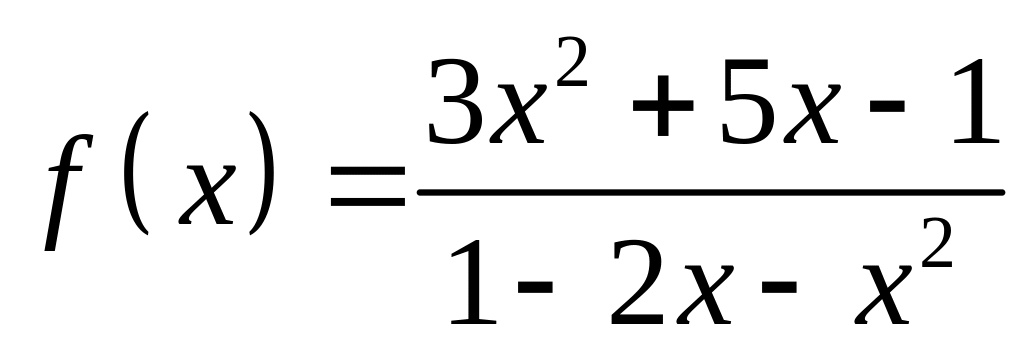
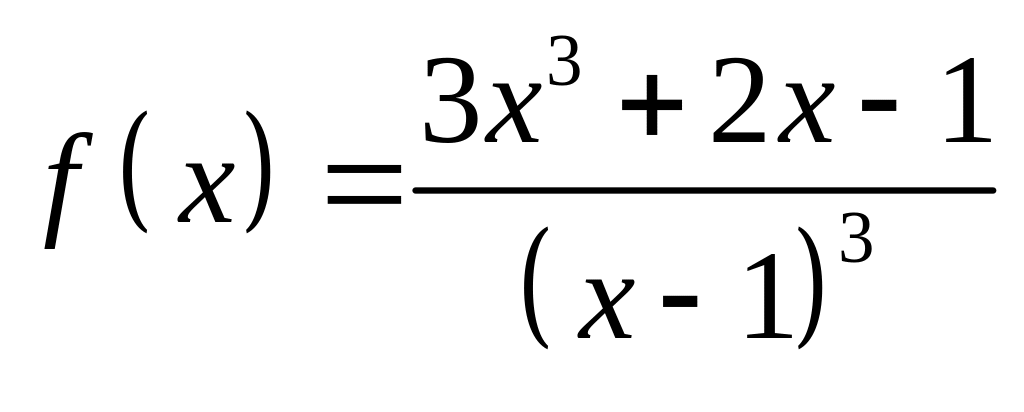
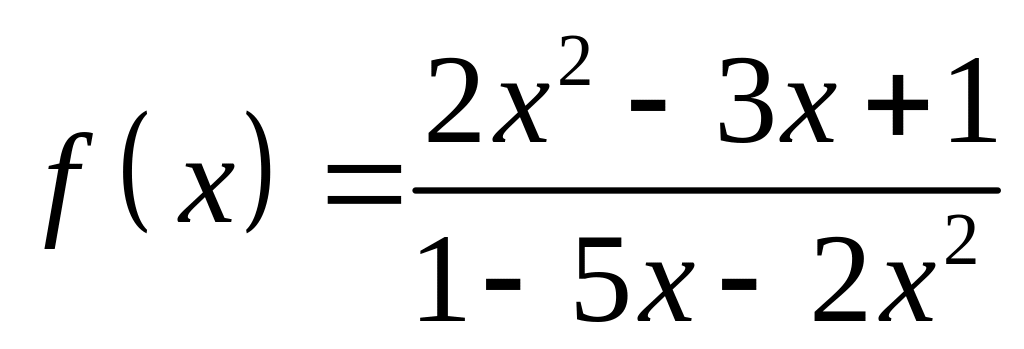
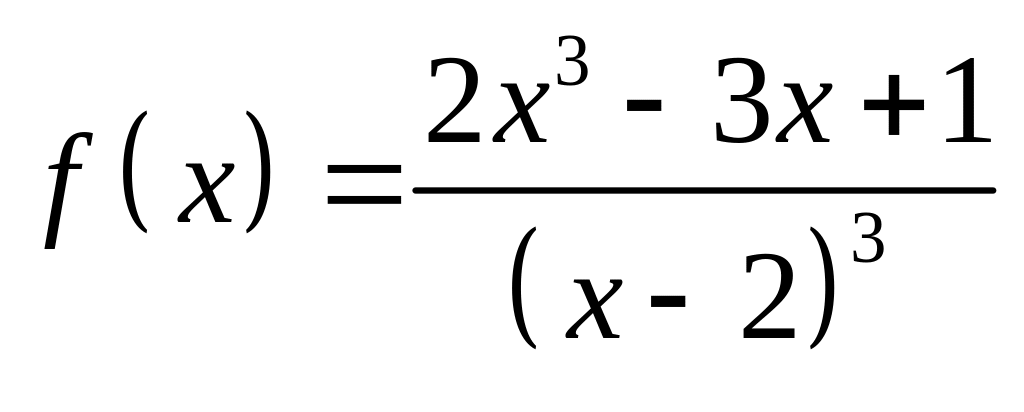
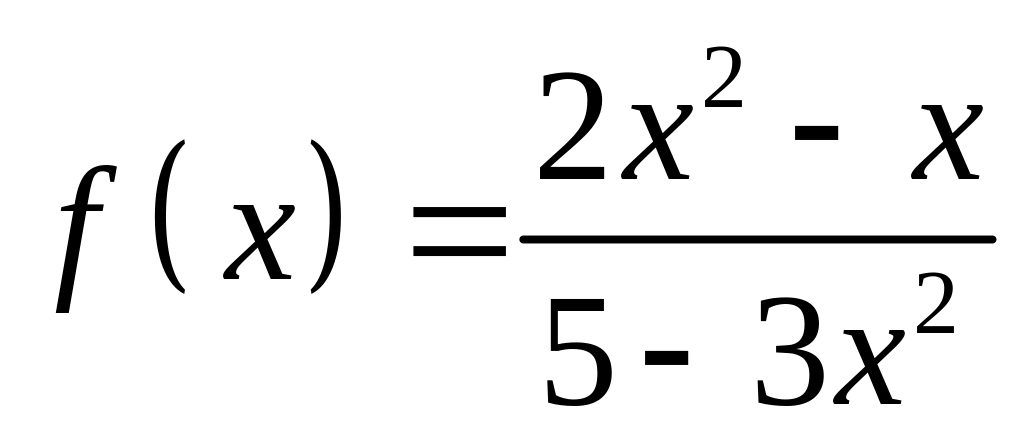
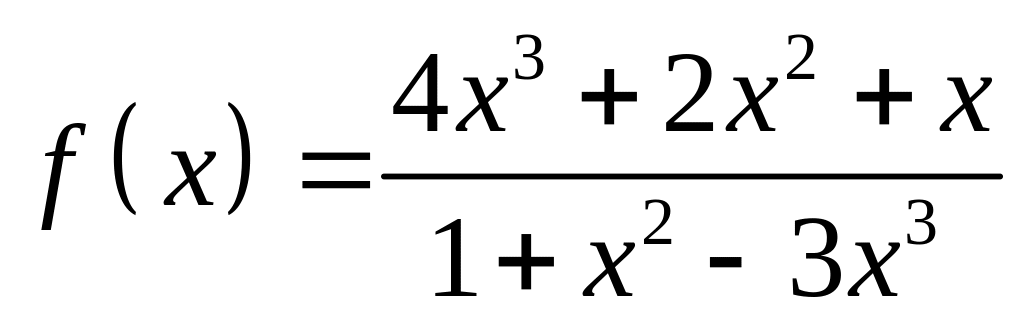
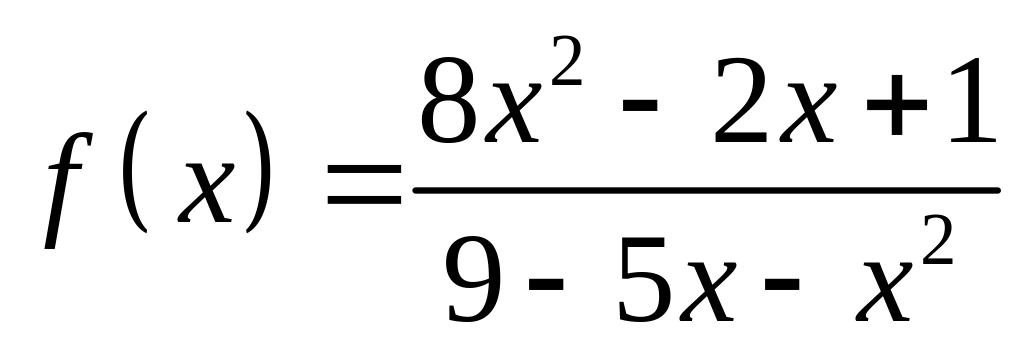
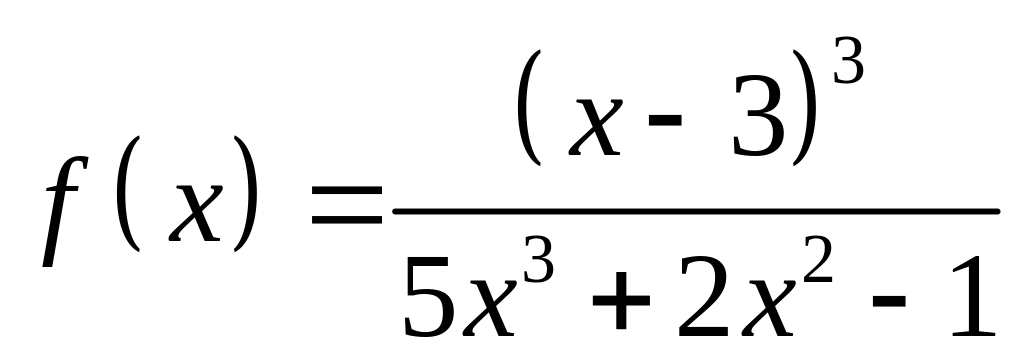
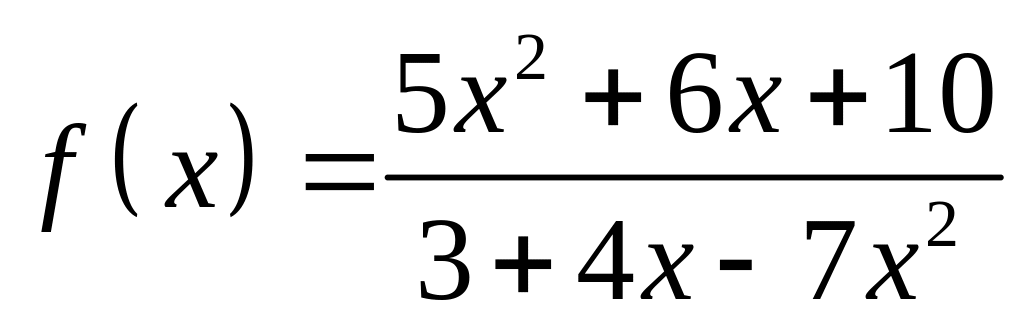
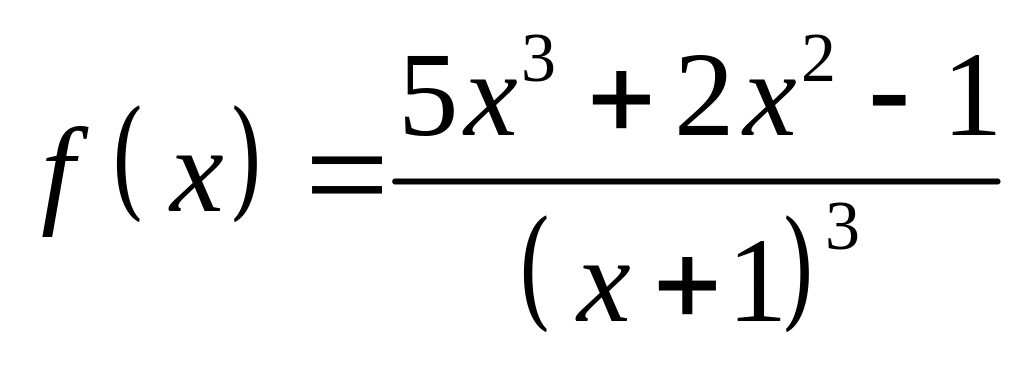
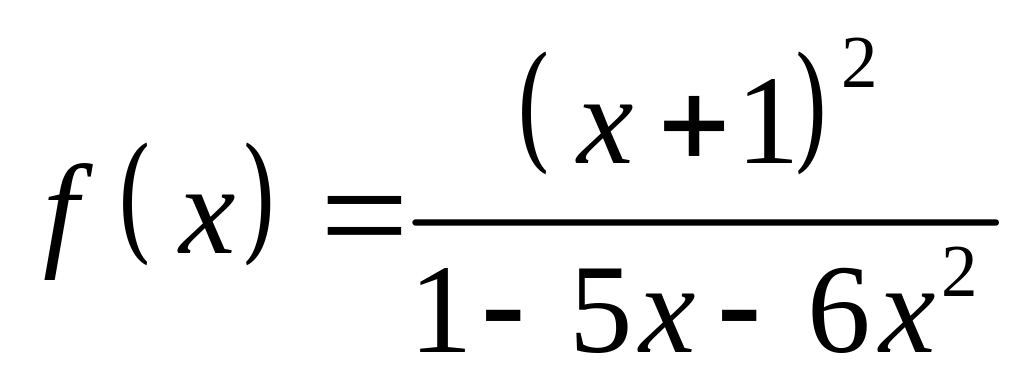
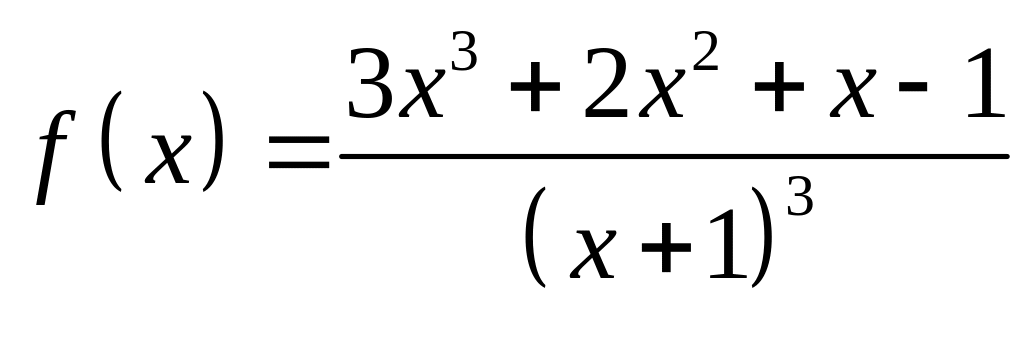
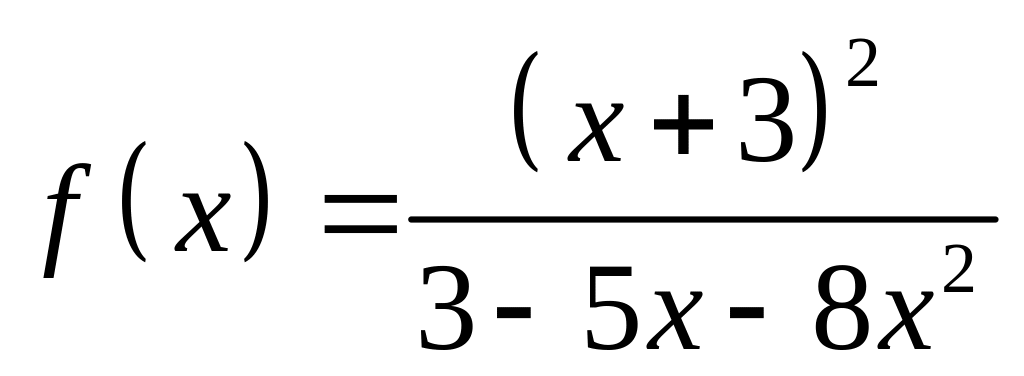
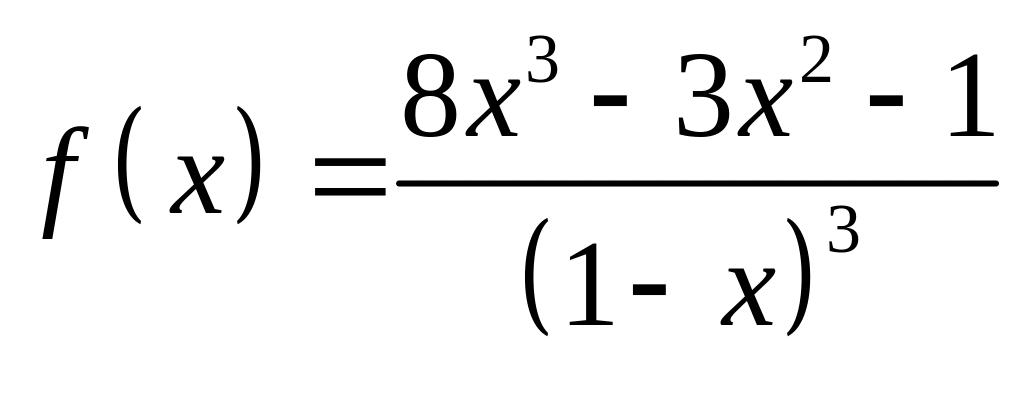
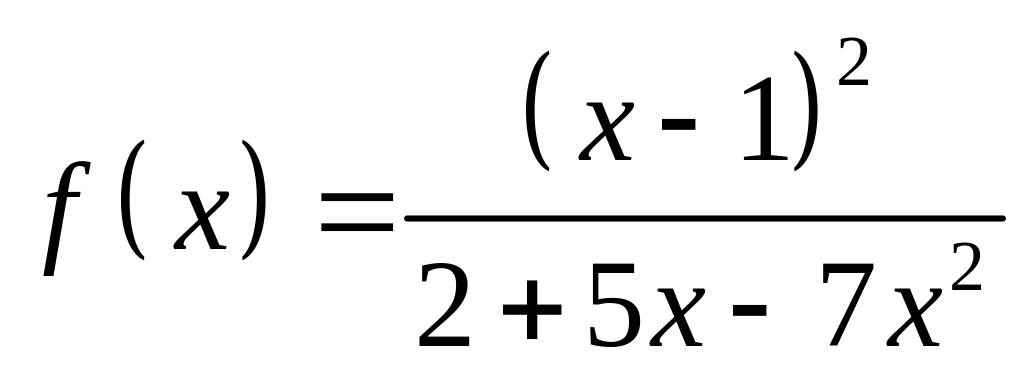
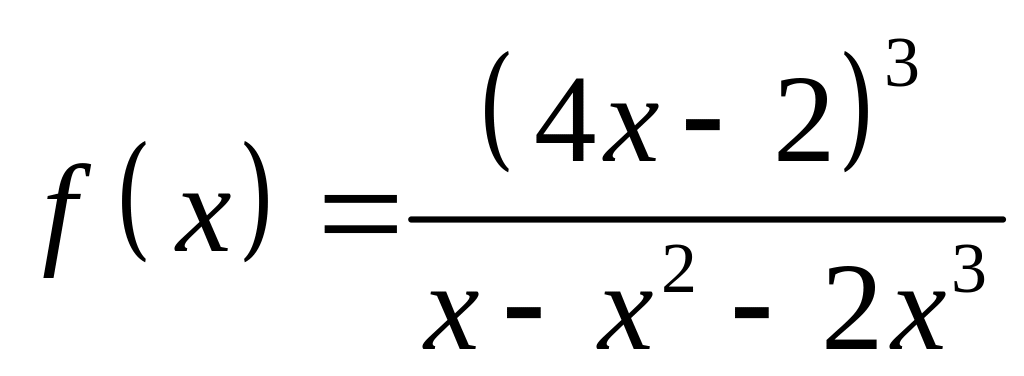
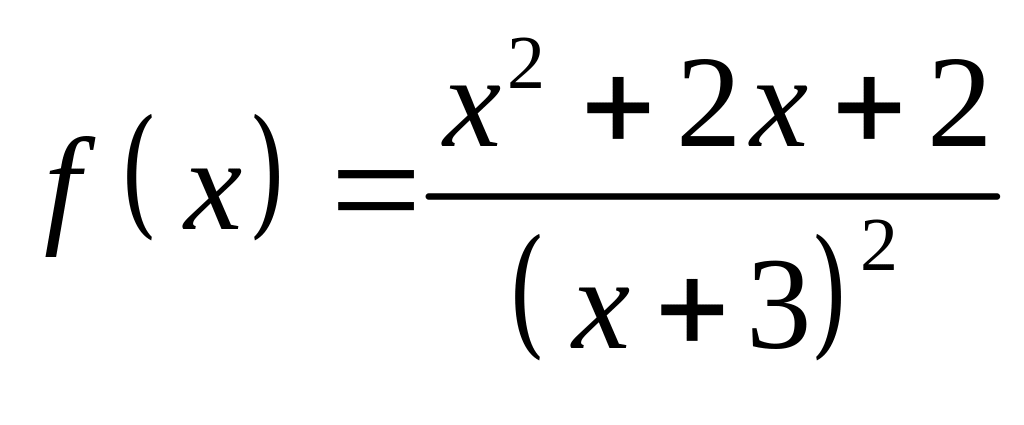
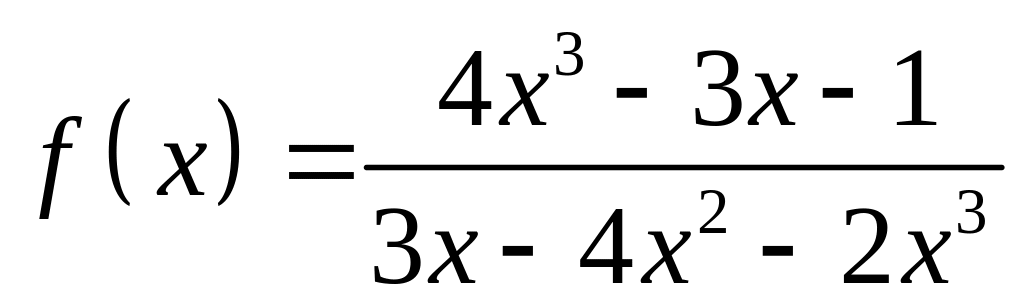
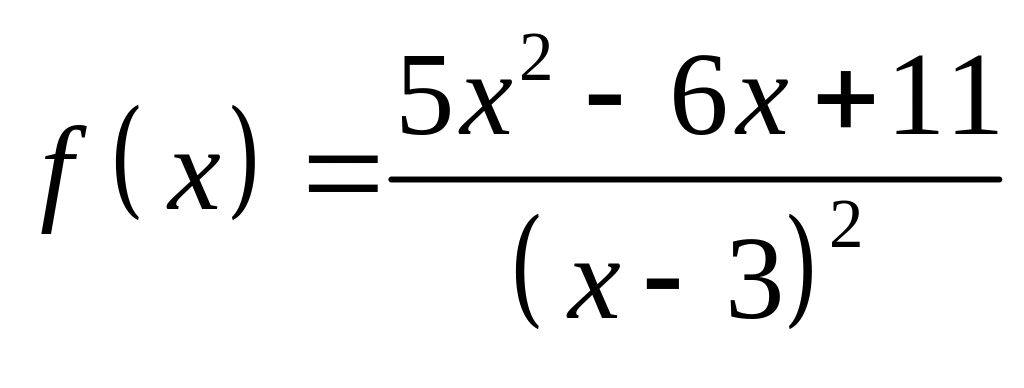
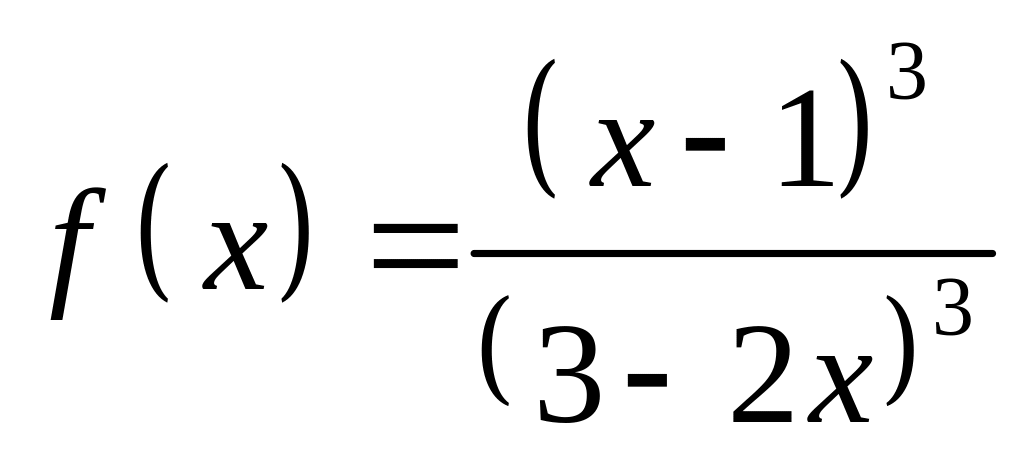
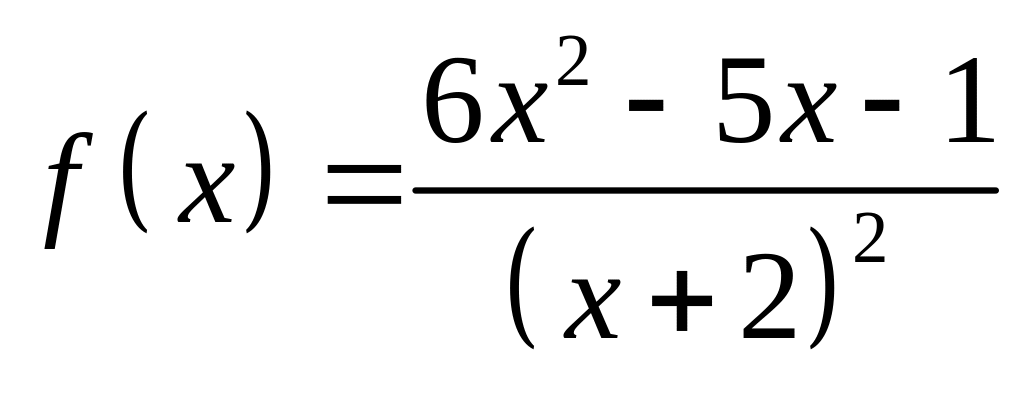
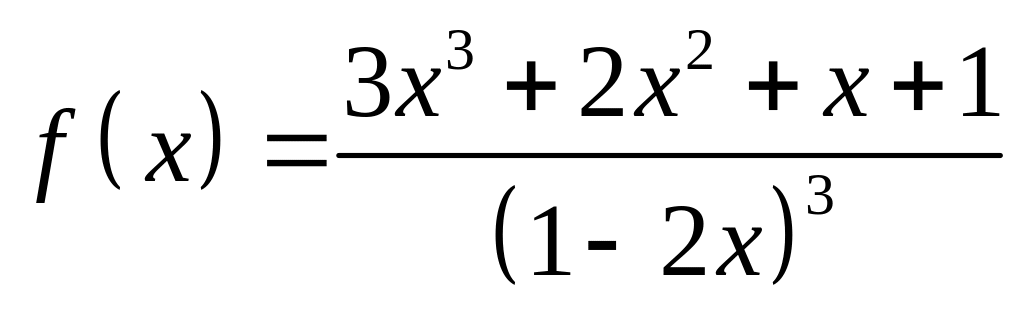
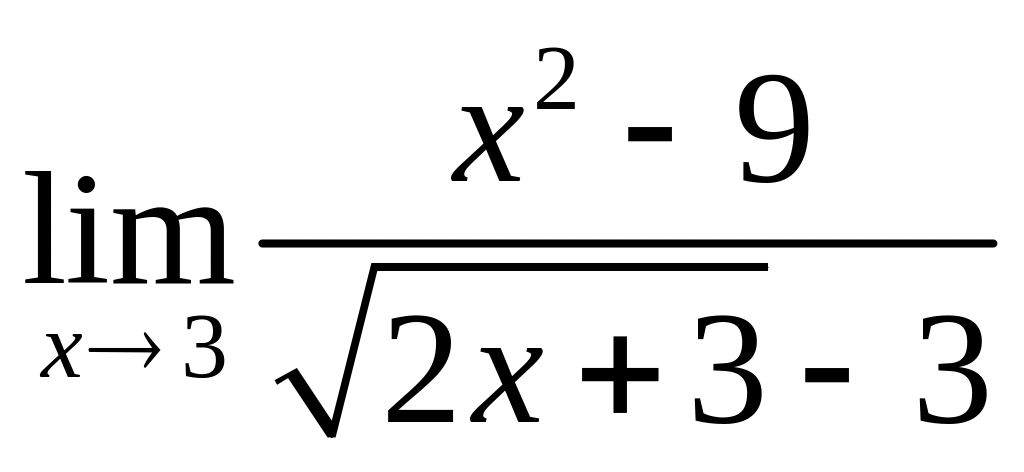
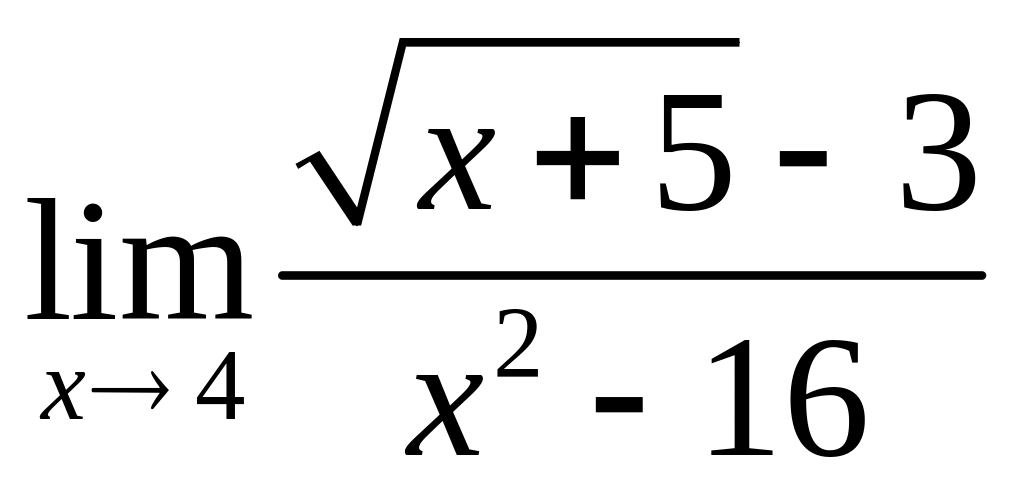

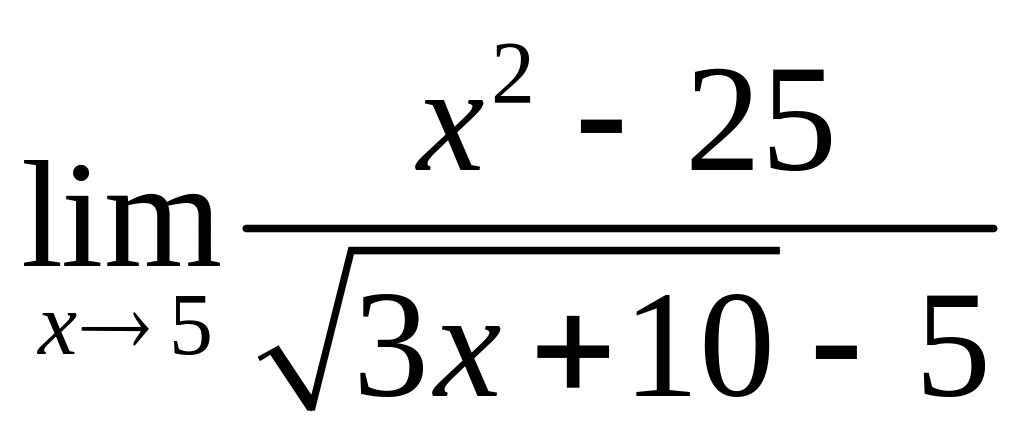
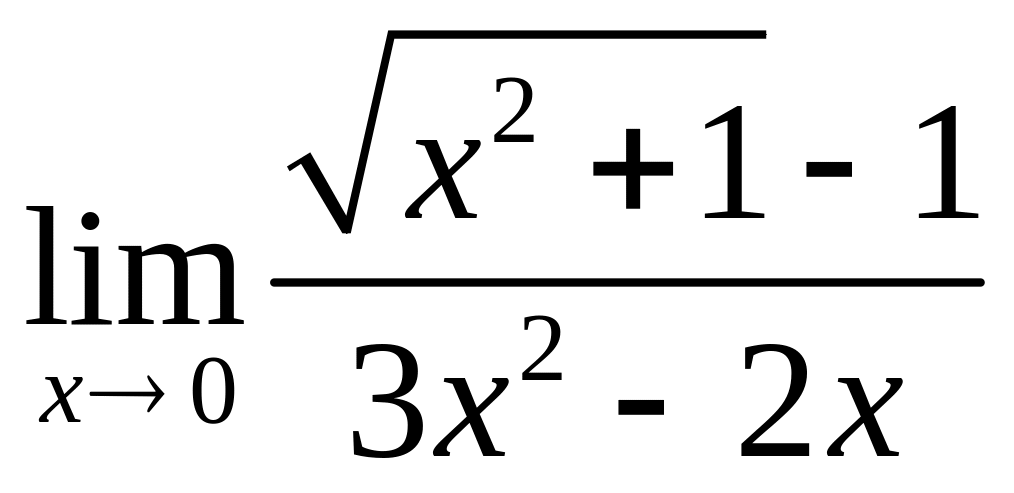
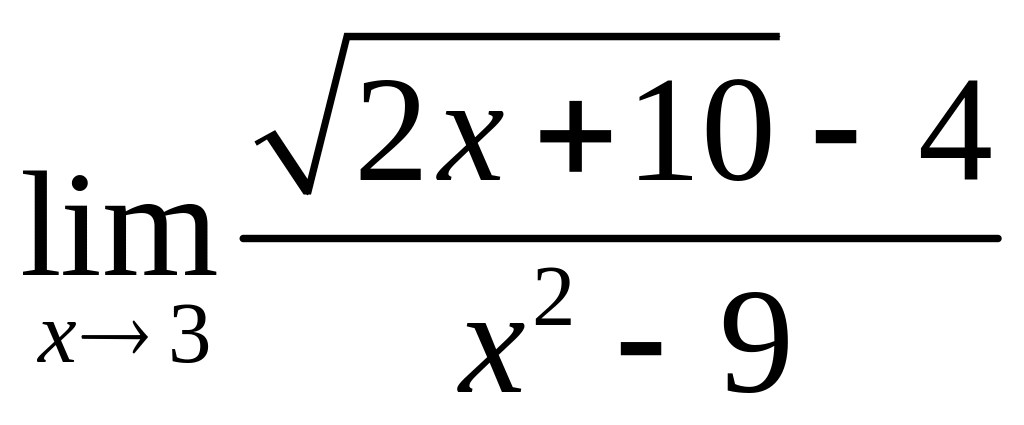
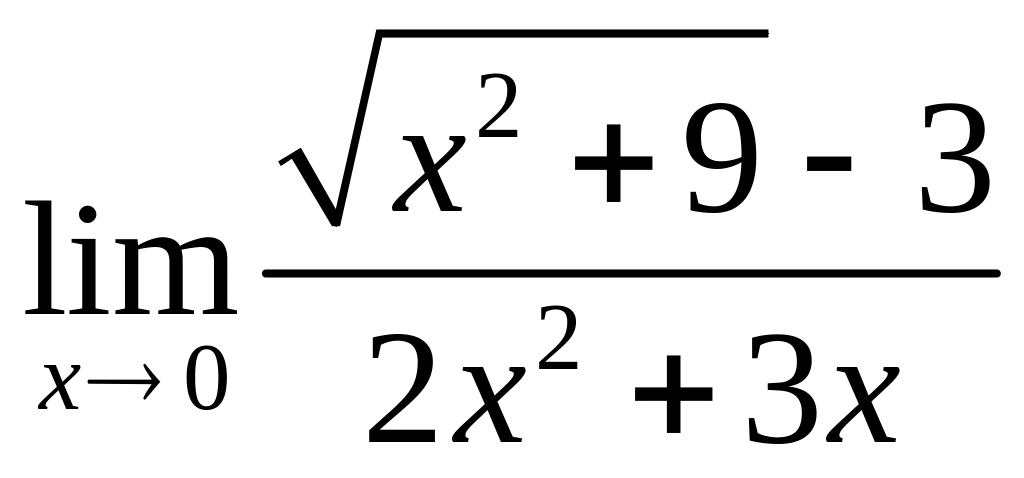
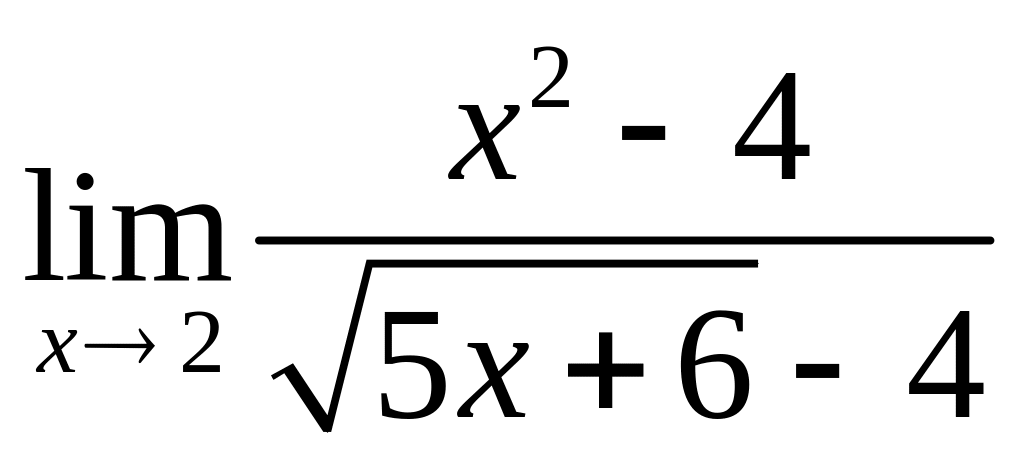

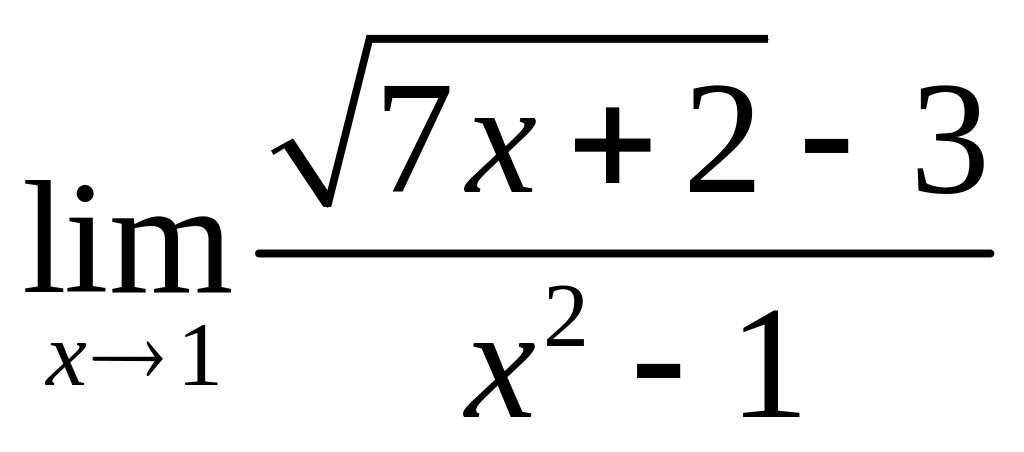
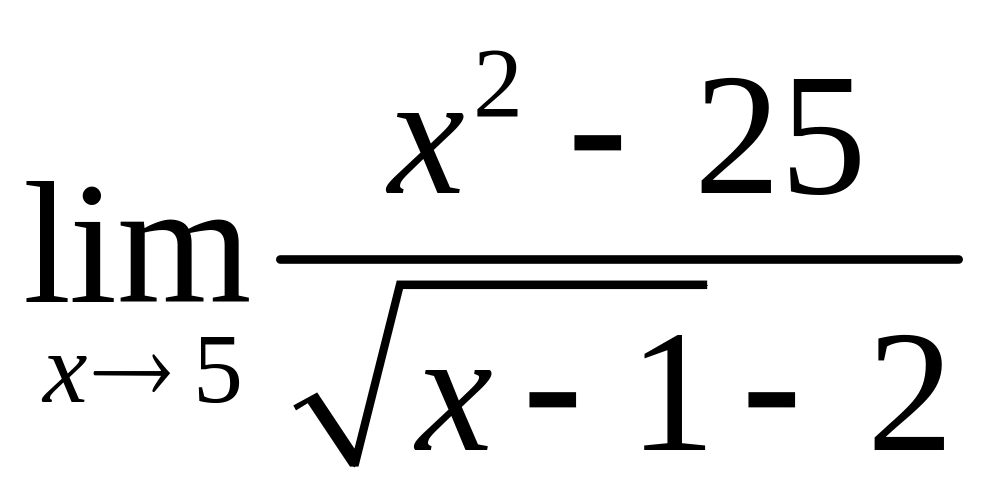
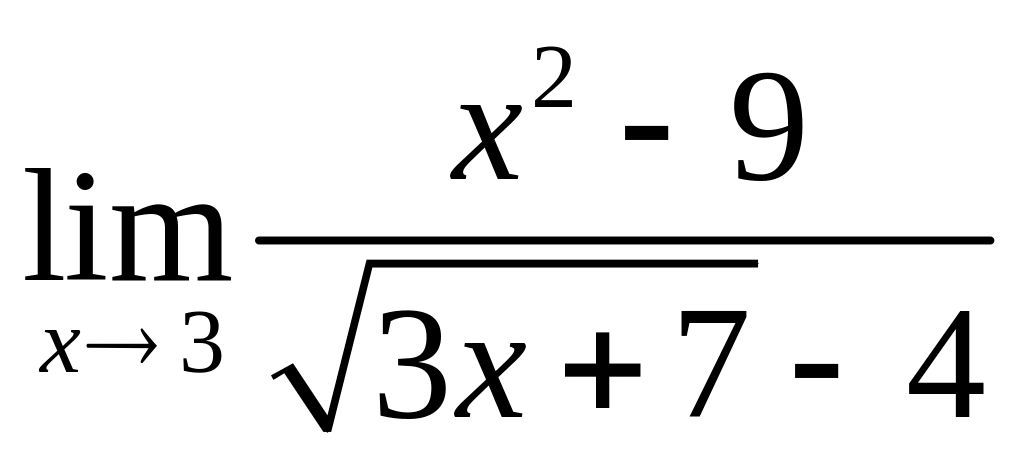
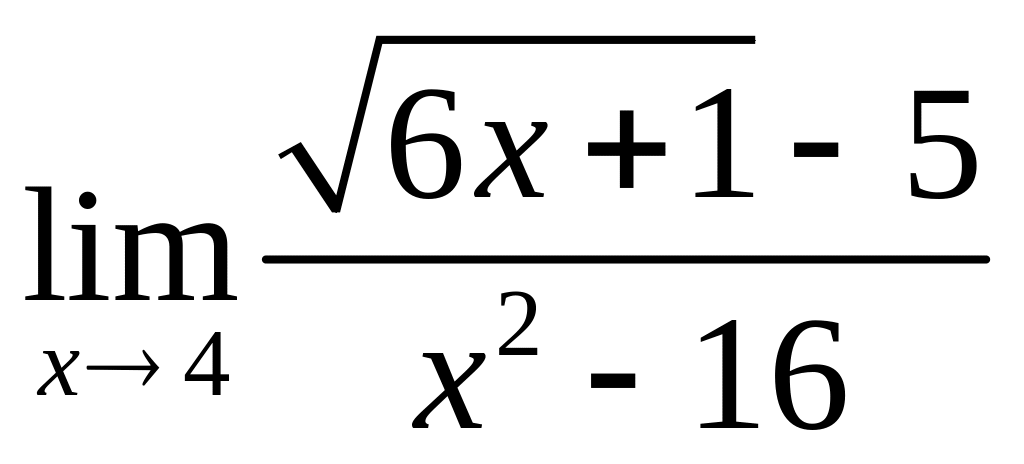
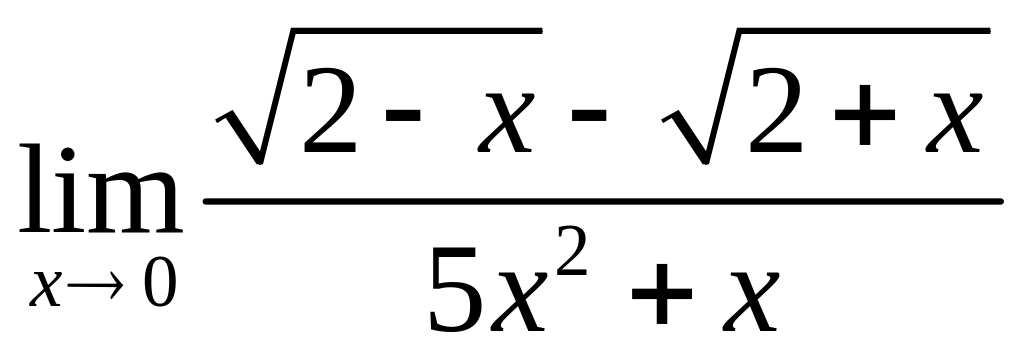
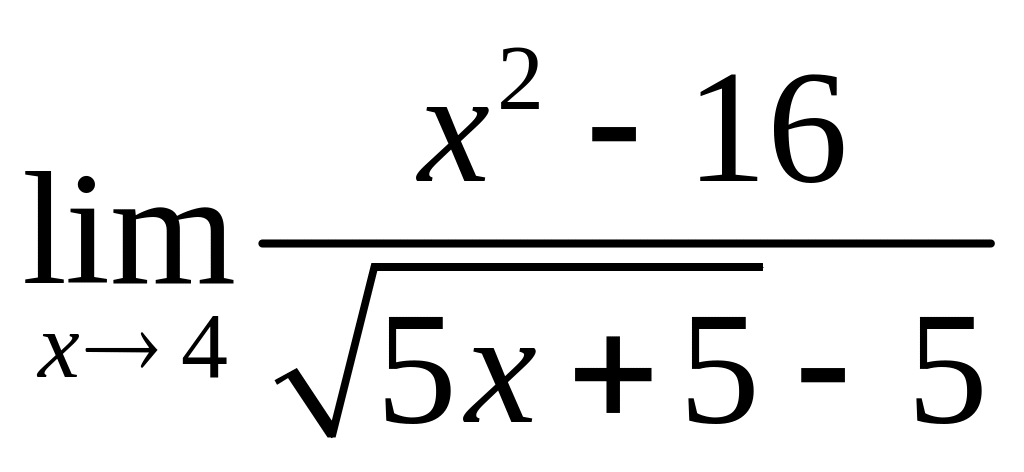
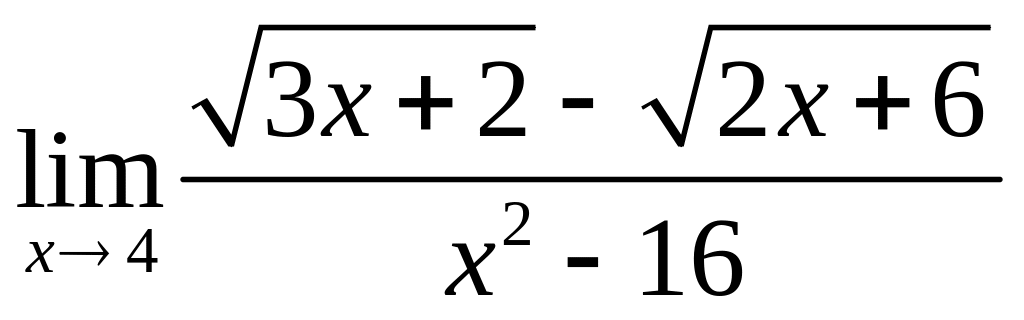
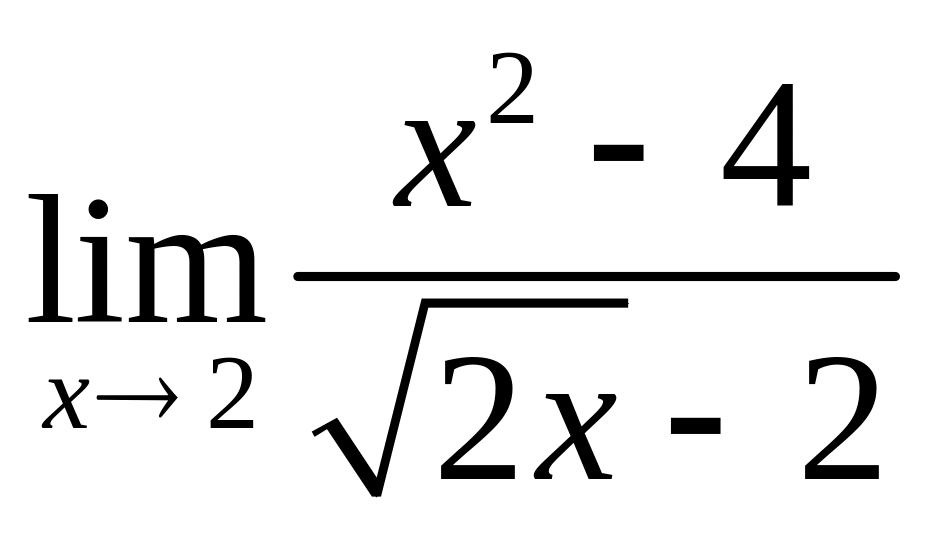
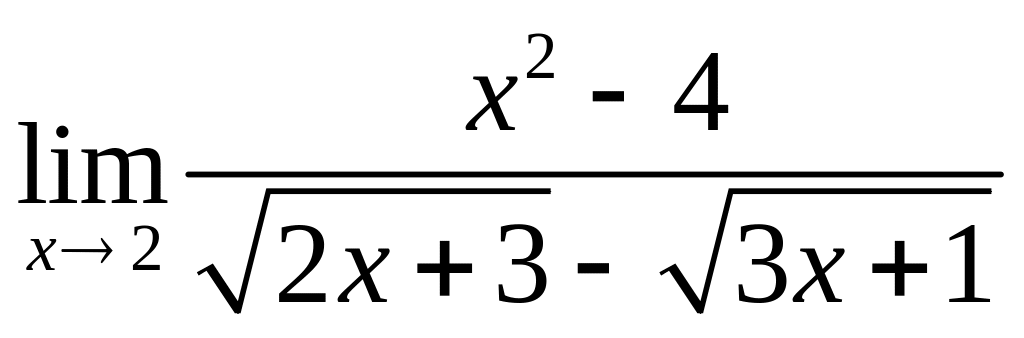

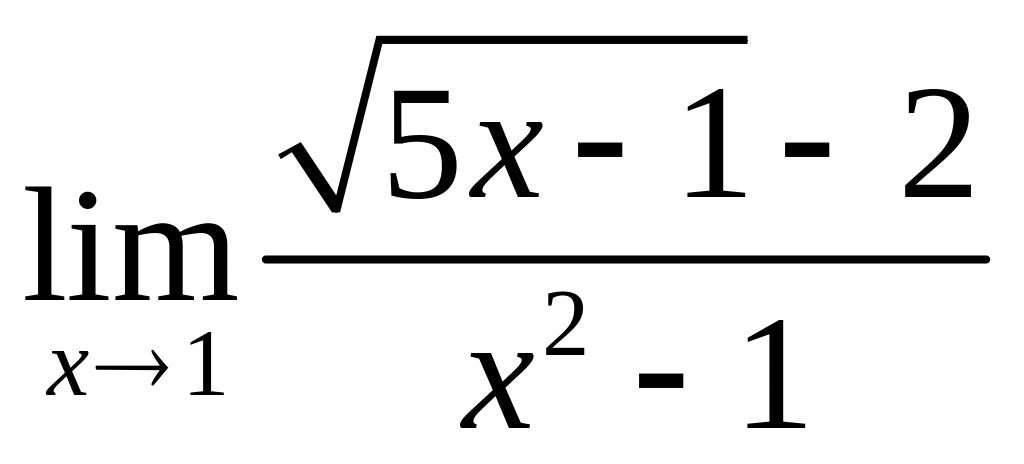
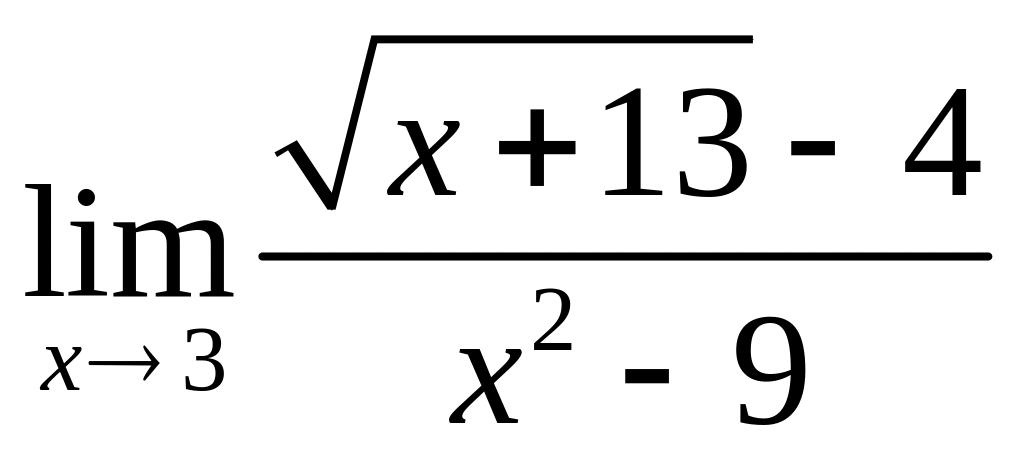

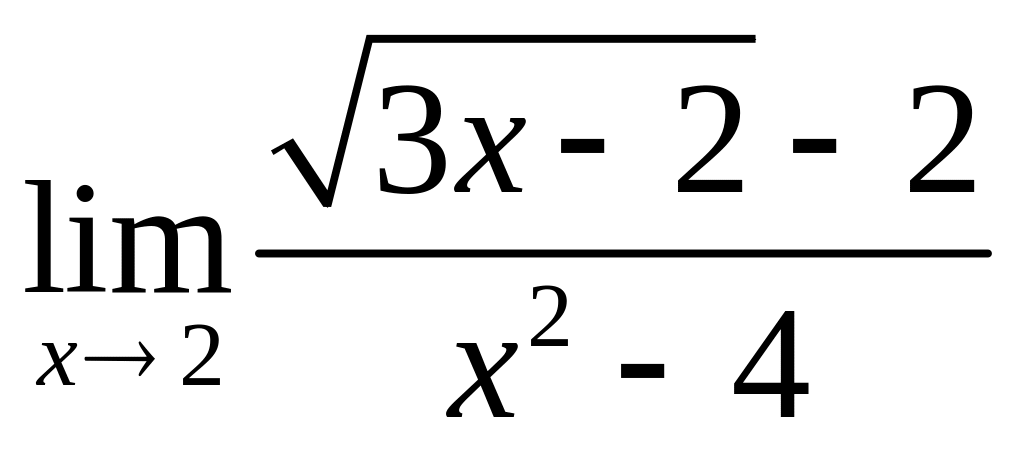
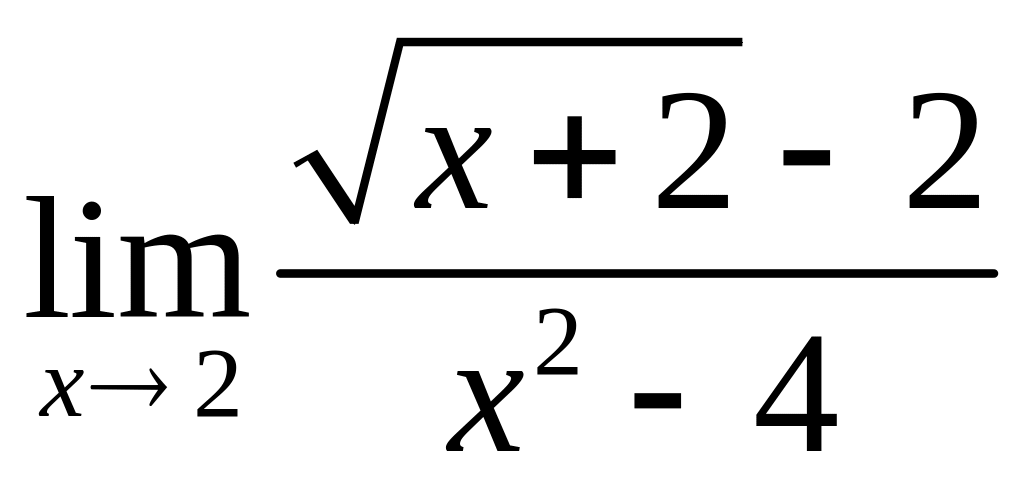
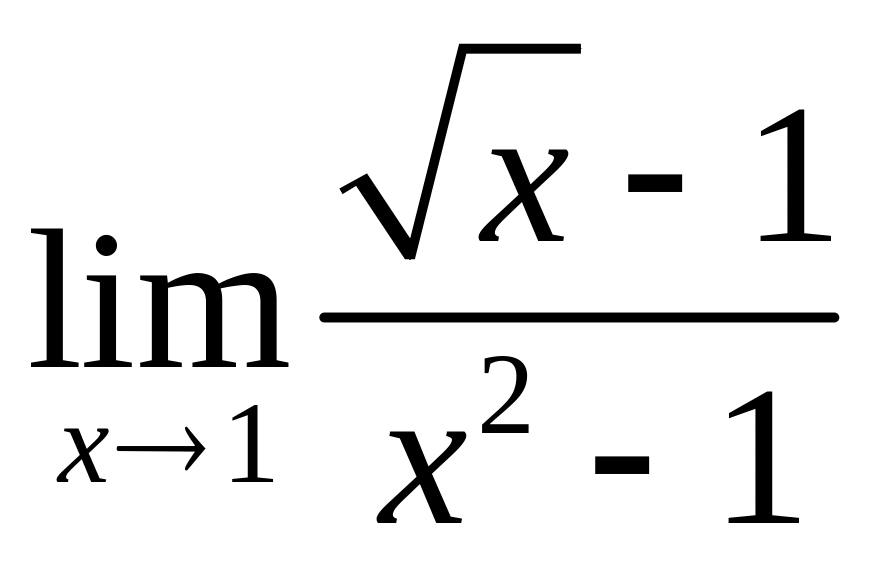
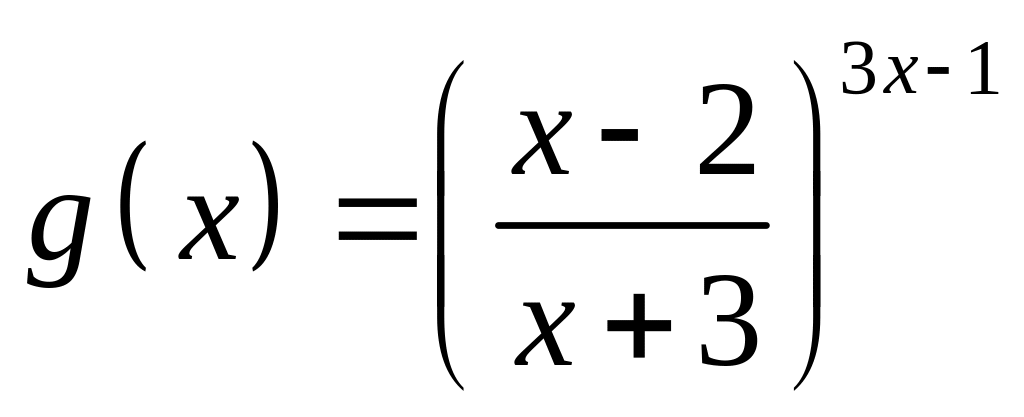
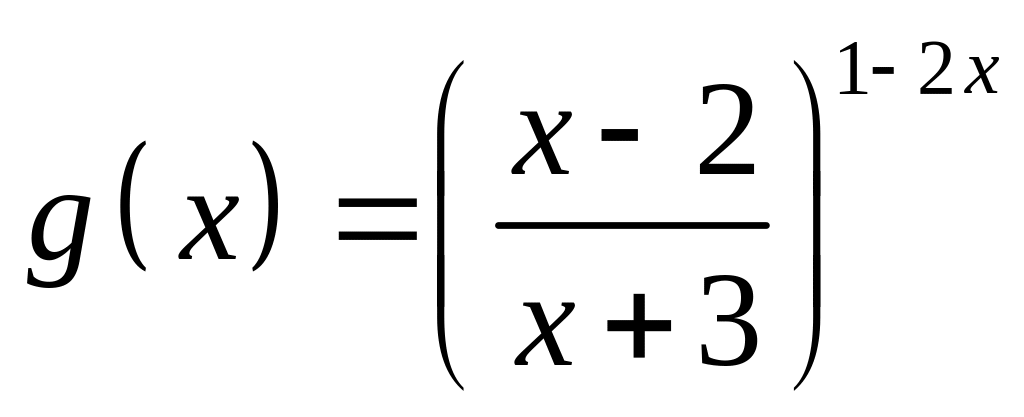
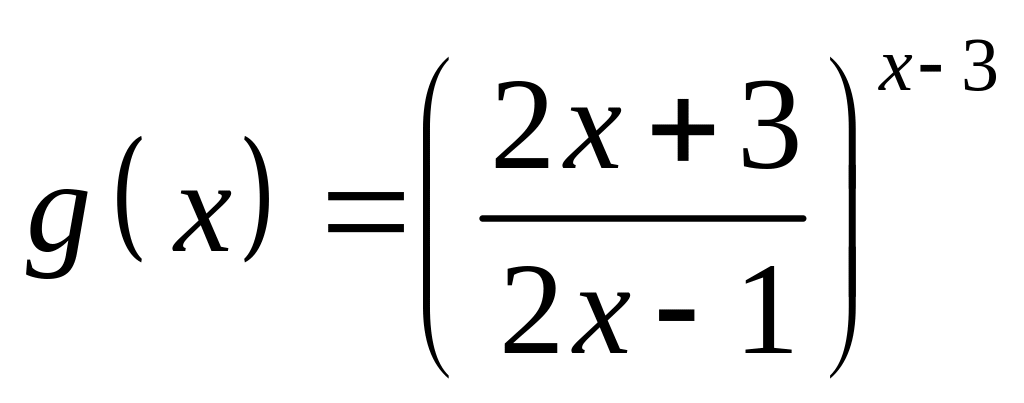
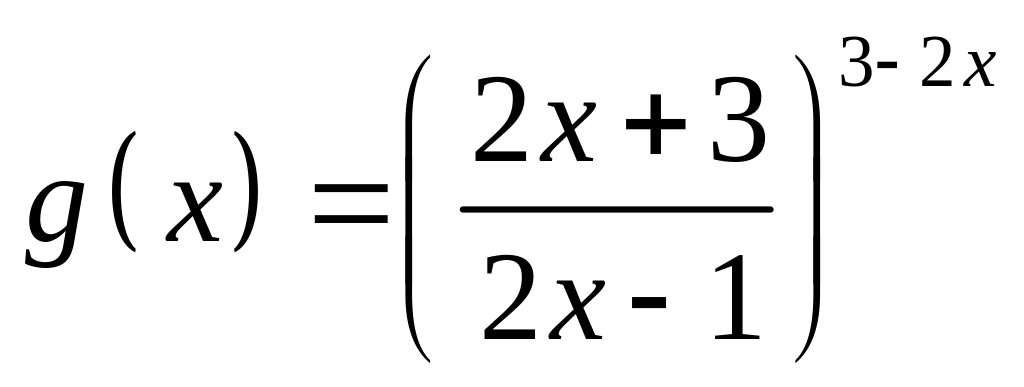
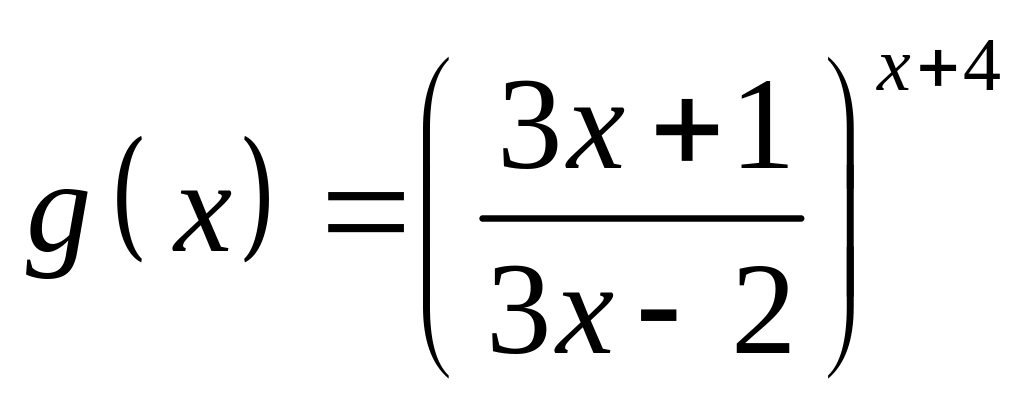
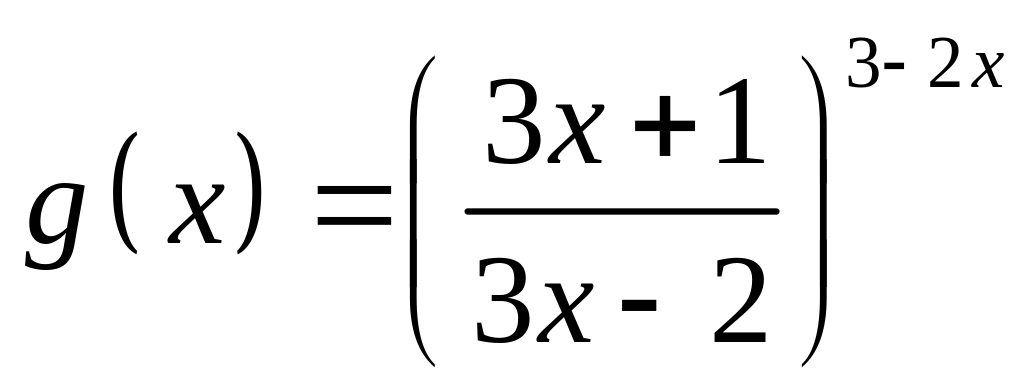


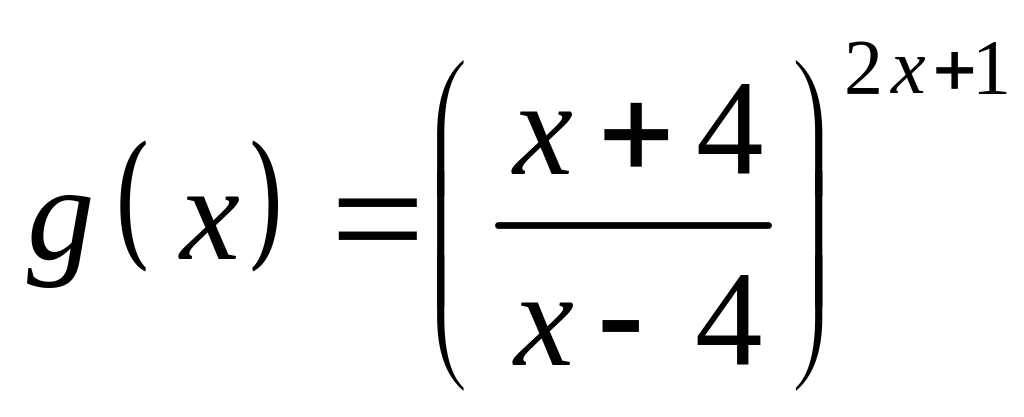
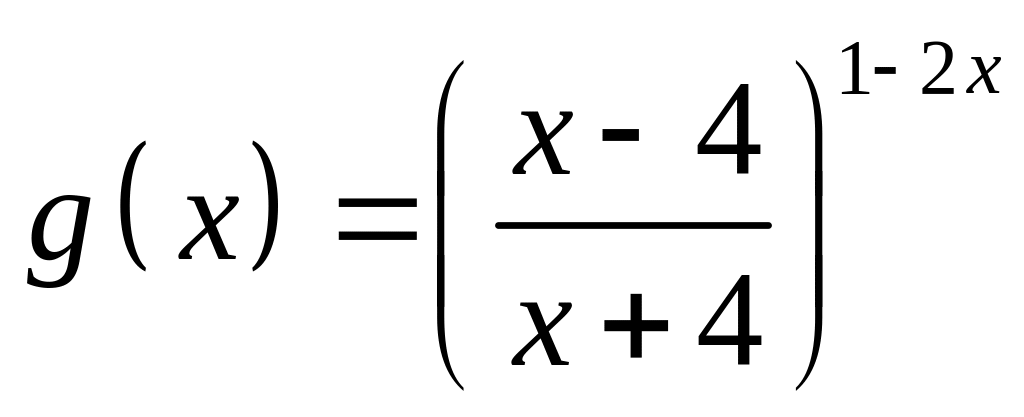
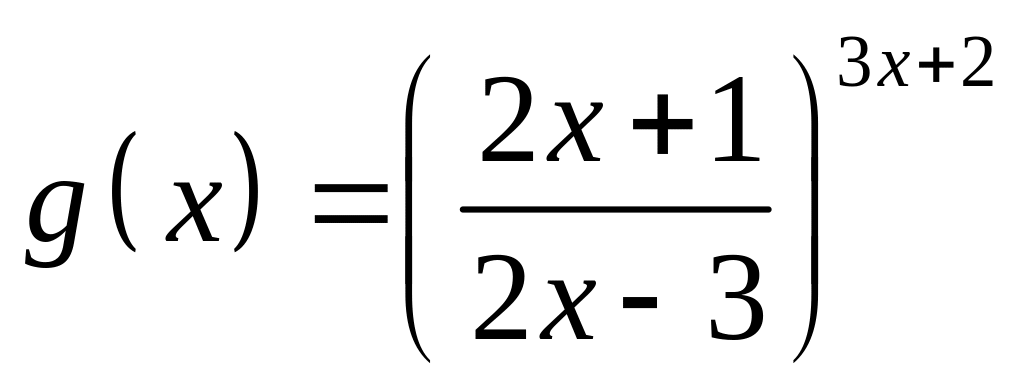
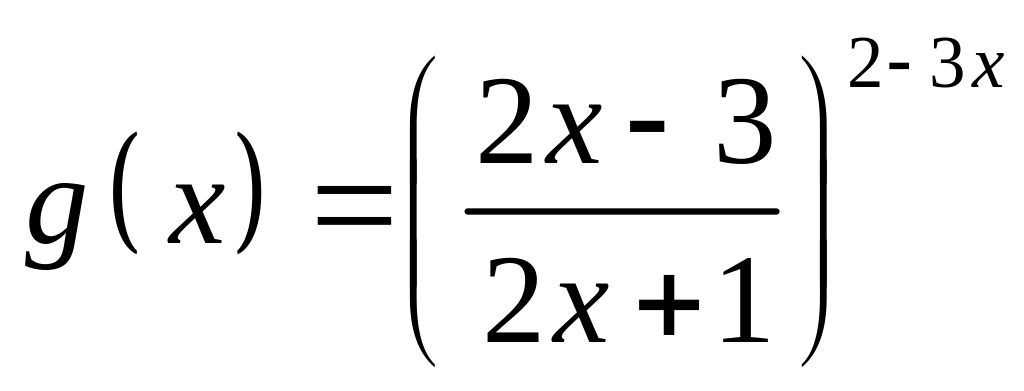
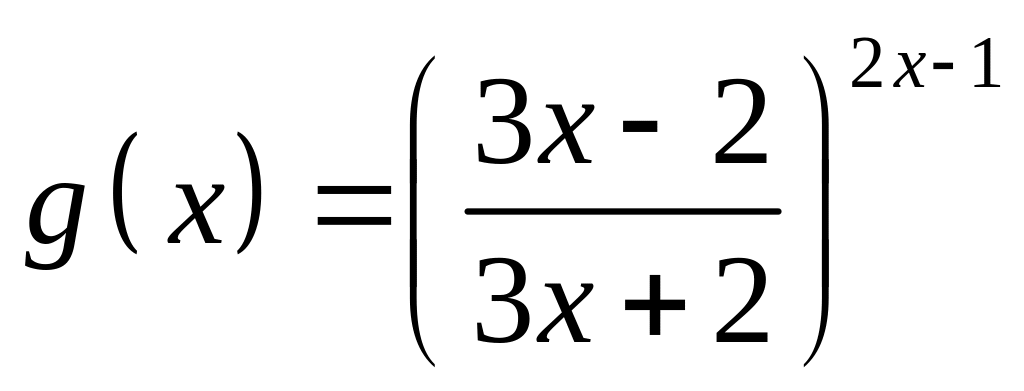
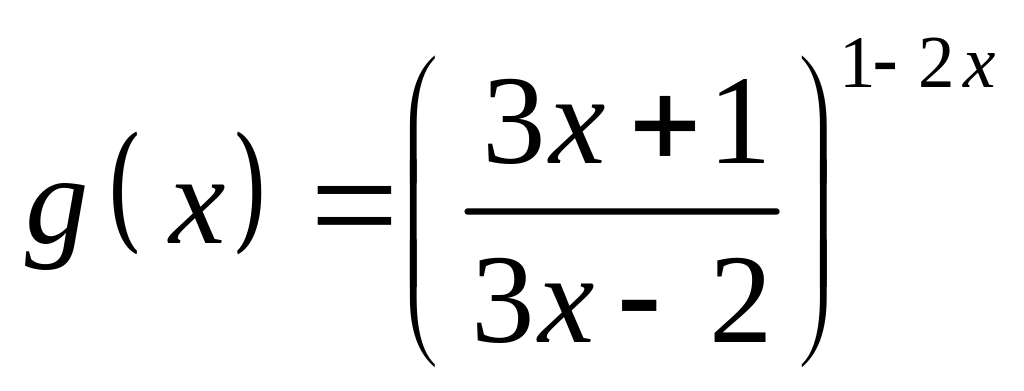

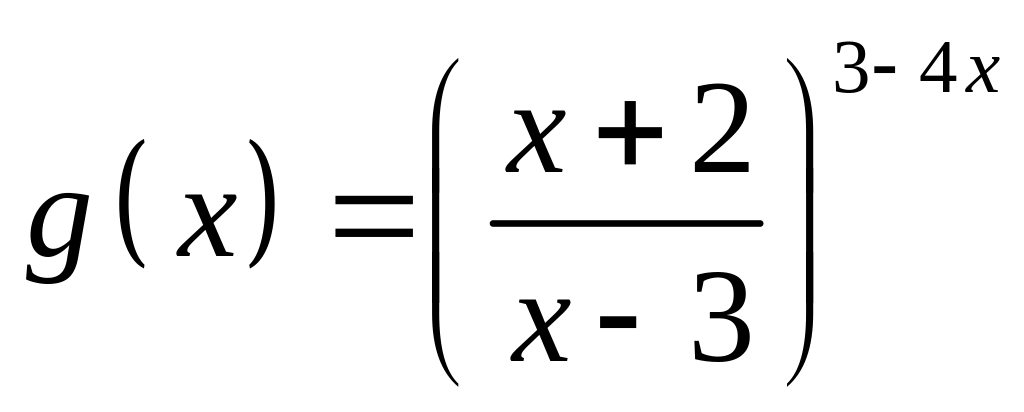
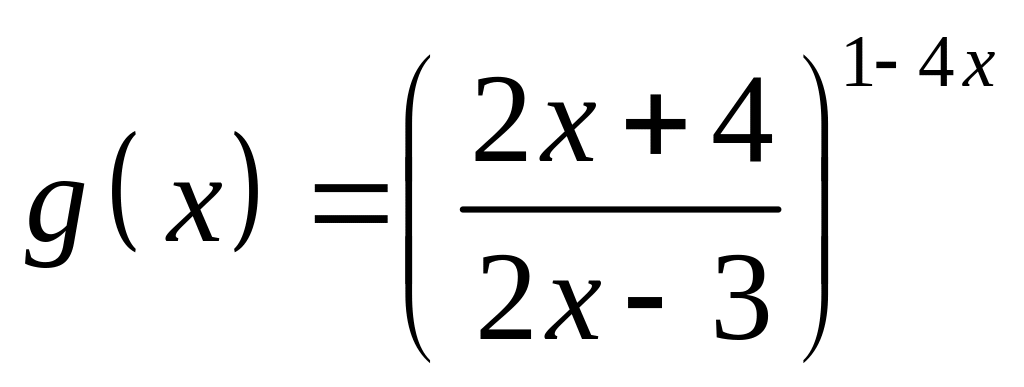
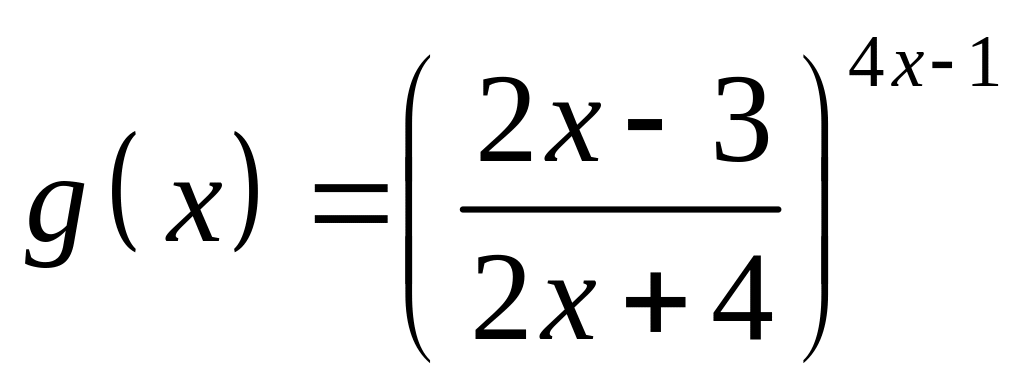
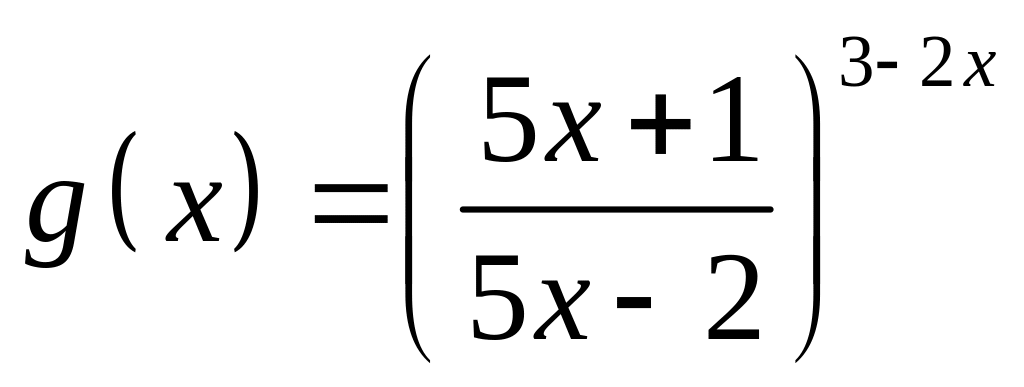
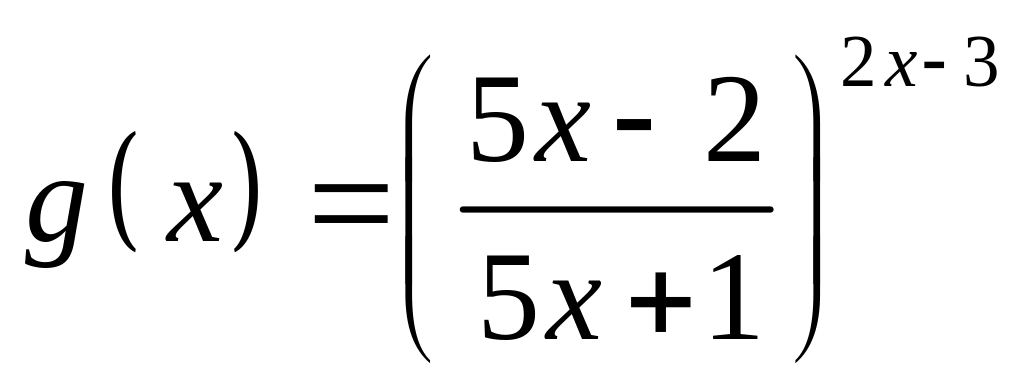
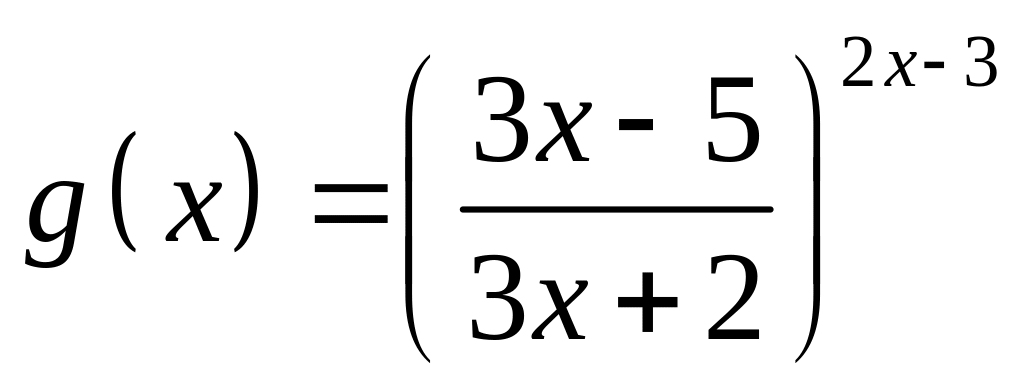

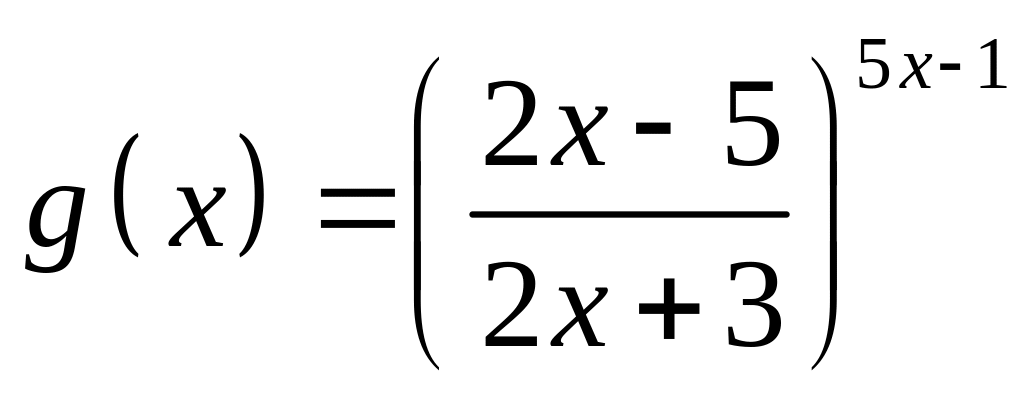
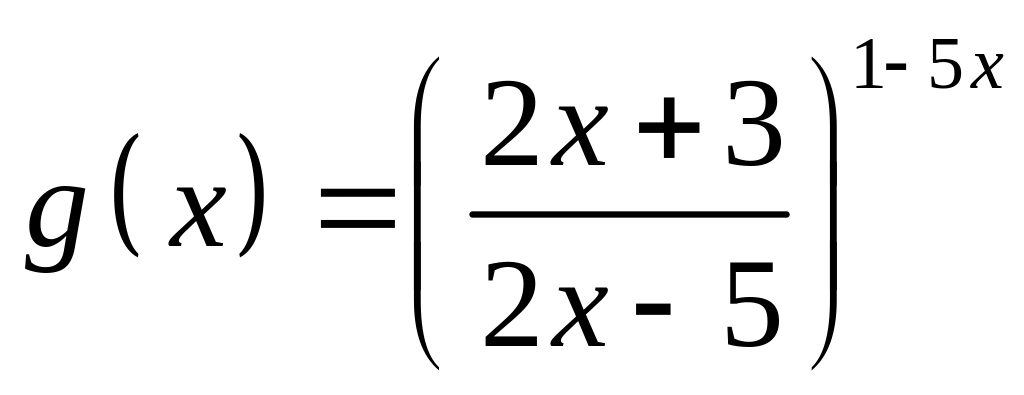
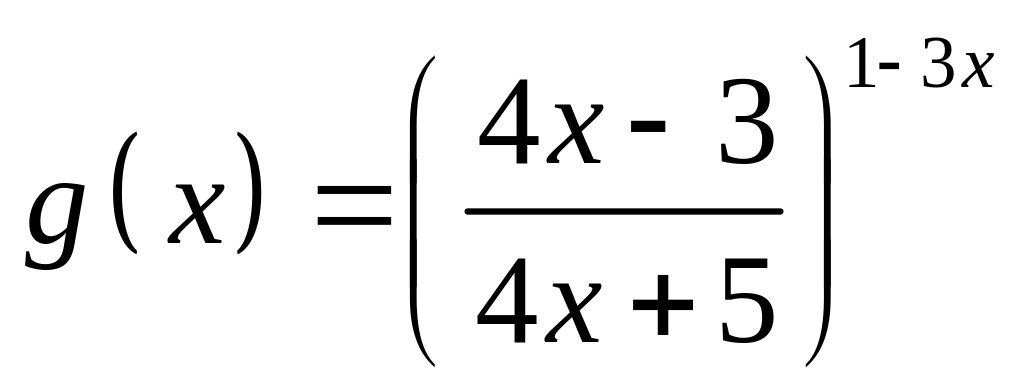
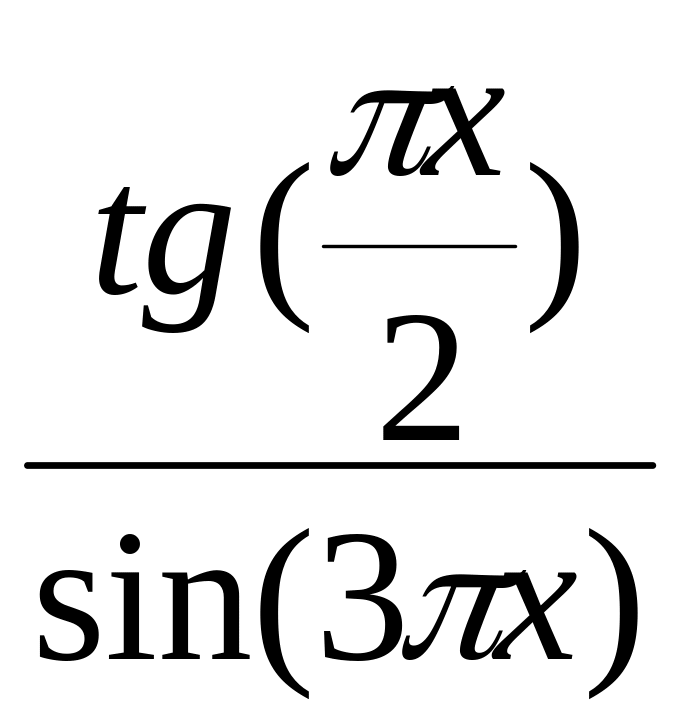 ;
;