Предварительный анализ:

1. Рёбра А1, В2, С3, D4, E5, F6 расположены перпендикулярно горизонтальной и параллельно фронтальной и профильной плоскости проекций. Каждое из этих рёбер спроецируется на горизонтальную плоскость проекций в виде точки, а на фронтальную и профильную плоскость проекций в виде прямых, перпендикулярных к оси проекций ОХ и ОY.

Рис.8,а

13

2. Грани BC23 и FE65 конгруэнтны* и параллельны фронтальной и перпендикулярны горизонтальной плоскостям проекций, в силу чего эти грани проецируются на фронтальную плоскость в виде фигуры, равной данным граням, а на горизонтальную плоскость – в виде прямых, параллельных оси проекций ОХ.

3. Верхняя грань ABCDEF, равная грани 123456, проецируется в такую же равную фигуру на горизонтальную плоскость проекций.

4. Рёбра ВС и FE, расположенные перпендикулярно профильной плоскости проекций, спроецируются на неё в виде точек, а на фронтальную плоскость проекций проецируются в натуральную длину в виде отрезков, равных данным.

Решение:

1. Вычерчиваем горизонтальную проекцию призмы, так как призма изо-

бразится на ней правильным шестиугольником. Проекции граней 123456 и ABCDEF на горизонтальной плоскости проекций совпадут.

2. На фронтальной плоскости проекций призма изобразится прямоугольником, разделённого на три части. Средняя часть определяет натуральную величину граней BC23 и FE65.

3. По двум проекциям строим третью проекцию (профильную).

_____________________________________________

* конгруэнтные фигуры ( от лат. conqruens, родительный падеж conqruentis -

соответствующий, совпадающий), геометрические фигуры, переходящие

друг в друга при движении.

14

Рис.8,б

2.1.2. Пирамида

Задача 1. Построим три проекции пирамиды, так чтобы два ребра SA и SD были параллельны фронтальной плоскости проекций, а основание было параллельно горизонтальной плоскости (рис.9,а,б).

Предварительный анализ:

1. Рёбра SA и SD, как параллельные фронтальной плоскости, спроецируются на ней в натуральную длину, а на горизонтальной плоскости – в виде прямых, параллельных ОХ.

15

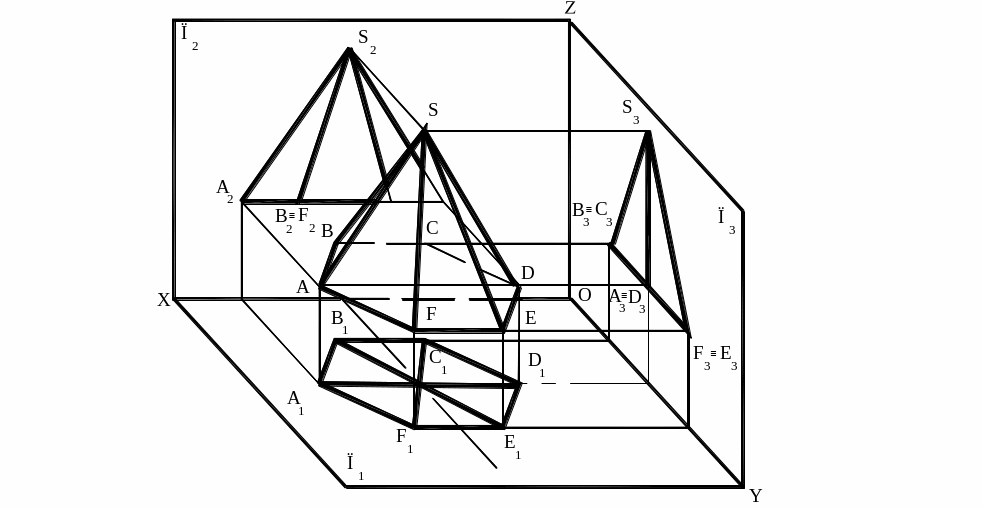
Рис. 9, а

2. Основание пирамиды спроецируется на плоскость П в натуральный размер, так как оно расположено параллельно горизонтальной плоскости проекций, а на фронтальную плоскость – в виде прямой, параллельной оси проекций.

3. Грани ASF, ASB, CSD и DSE находятся в общем положении, так как они наклонны ко всем плоскостям проекций.

4. Грани BSC и FSE перпендикулярны профильной плоскости проекций П3.

16

Рис. 9, б

Решение:

1. Начинаем вычерчивать с горизонтальной проекции, так как пирамида изобразится на ней правильным шестиугольником и линиями SA, SB, SC, SD, SE и SF, соединяющими вершину пирамиды S с точками основания.

17

2. На фронтальной плоскости проекций пирамиды изобразится в виде треугольника A2S2D2 и рёбер B2S2≡F2S2, C2S2≡E2S2, попарно и линий связи.

3. На фронтальной плоскости проекций пирамиды изобразится в виде треугольника A2S2D2 и рёбер B2S2≡ F2S2, C2S2≡ E2S2, попарно совмещённых.

4. Третья проекция строится при помощи постоянной прямой и линий связи.

Задача 2. На горизонтальной проекции пирамиды (см. рис.9) дана проекция L точки L. Требуется найти фронтальную проекцию данной точки.

Каждая точка находится при помощи прямой, лежащей в плоскости или образующей, так как точка, принадлежащая плоскости лежит на линии, принадлежащей также данной плоскости.