
- •Учебно-методические материалы к изучению дисциплины «Методы оптимизации» (конспект лекций)
- •1. Классификация задач оптимизации
- •2. Классификация математических методов и моделей в экономике
- •3. Линейное программирование
- •3.1. Постановка задачи линейного программирования
- •3.2. Экономическая интерпретация задач линейного программирования
- •3.3. Требования совместности условий
- •3.4. Графический метод решения задач линейного программирования
- •3.5. Симплекс-метод
- •3.6. Модифицированный симплекс-метод
- •3.7. Построение опорных планов
- •3.8. Условия оптимальности
- •3.9. Метод искусственного базиса
- •3.10. Транспортная задача
- •3.11. Двойственные задачи линейного программирования
- •3.12. Устойчивость оптимизационного решения
- •4. Нелинейное программирование
- •4.1. Классификация и общая постановка задач нелинейного программирования
- •4.2. Метод множителей Лагранжа
- •4.3. Возможные обобщения метода множителей. Седловая точка функции Лагранжа
- •4.4. Оптимальные решения при ограничениях-неравенствах. Теорема Куна - Таккера
- •4.5. Выпуклое программирование. Задача выпуклого программирования
- •4.6. Квадратичное программирование
- •4.7. Градиентные методы
- •5. Оптимизация на графах
- •5.1. Основные понятия теории графов
- •5.2. Связность
- •5.3. Подграфы
- •5.4. Матрица графов
- •5.5. Потоки в сетях
- •5.6. Задача о максимальном потоке сети
- •5.7. Задача о кратчайшем пути
- •5.8. Задача коммивояжера
- •5.9. Оптимизация сетевого графика
- •5.10. Методы оптимизации производственной программы
- •6. Динамическое программирование
- •6.1. Общая постановка задачи динамического программирования
- •6.2. Принцип оптимальности. Уравнение Беллмана
- •6.3. Простейшие экономические задачи, решаемые методом динамического программирования
- •7. Математические модели потребительского поведения и спроса
- •7.1. Отношение предпочтения и функция полезности
- •7.2. Решение задачи об оптимальном выборе потребителя
- •7.3. Функции спроса. Коэффициент эластичности
3.6. Модифицированный симплекс-метод
Основная идея модифицированного
симплекс-метода заключается в использовании
текущей обратной матрицы
![]() (и
исходных данных задачи) при выполнении
вычислений, необходимых для определения
включаемой и исключаемой переменных.
Представление обратной матрицы в
мультипликативной форме позволяет
вычислять последовательность обратных
матриц непосредственно по исходным
данным без использования многократных
операций обращения каждого базиса. Как
и в обычном симплекс-методе, в данном
случае исходный базис всегда представляет
собой единичную матрицу I, обратной
к которой является сама эта матрица.
Поэтому, если
(и
исходных данных задачи) при выполнении
вычислений, необходимых для определения
включаемой и исключаемой переменных.
Представление обратной матрицы в
мультипликативной форме позволяет
вычислять последовательность обратных
матриц непосредственно по исходным
данным без использования многократных
операций обращения каждого базиса. Как
и в обычном симплекс-методе, в данном
случае исходный базис всегда представляет
собой единичную матрицу I, обратной
к которой является сама эта матрица.
Поэтому, если
![]() - последовательность матриц, а
- последовательность матриц, а
![]() - последовательность обратных матриц,
то
- последовательность обратных матриц,
то
![]()
Последовательность подстановок приводит к следующей формуле:
![]()
Следует подчеркнуть, что мультипликативное представление обратной матрицы не является необходимой процедурой для реализации вычислительной схемы модифицированного симплекс-метода, и на каждой итерации можно применять любой из способов обращения текущего базиса. При использовании модифицированного симплекс-метода важно то, что обратные матрицы вычисляются способом, позволяющим уменьшить влияние машинных ошибок округления.
Шаги алгоритма модифицированного симплекс-метода, по существу, такие же, как и в алгоритме обычного симплекс-метода.
3.7. Построение опорных планов
Рассмотрим каноническую форму задачи линейного программирования
![]() (1)
(1)
при ограничениях
![]()
![]()
Пусть
![]() . Предположим, что система ограничений
содержит m - единичных векторов.
Пусть это первые n - векторов, тогда:
. Предположим, что система ограничений
содержит m - единичных векторов.
Пусть это первые n - векторов, тогда:
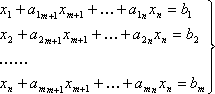 (2)
(2)
![]() (3)
(3)
Запишем систему (2) в векторной форме
![]() (4)
(4)
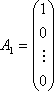 ,
,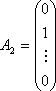 ,
,
 .
.
Векторы
![]() - единичные, линейно независимые векторы
m - мерного пространства, они образуют
базис. В (4) за базисные неизвестные
выберем
- единичные, линейно независимые векторы
m - мерного пространства, они образуют
базис. В (4) за базисные неизвестные
выберем
![]() . Свободные неизвестные приравниваем
нулю и учитывая, что
. Свободные неизвестные приравниваем
нулю и учитывая, что
![]() (где
(где
![]() ),
а векторы - единичные. Получим
первоначальный план
),
а векторы - единичные. Получим
первоначальный план
![]() (5).
(5).
Плану (5) соответствует разложение
![]() (6), так как
- линейно независимые, то первоначальный
план является и опорным.
(6), так как
- линейно независимые, то первоначальный
план является и опорным.
Рассмотрим, как исходя из опорного
плана (5) можно построить другой опорный
план
- базис, поэтому
![]() .
Предположим, что для некоторого вектора,
не входящего в базис, например для
.
Предположим, что для некоторого вектора,
не входящего в базис, например для
![]() ,
является положительным хотя бы один из
коэффициентов
,
является положительным хотя бы один из
коэффициентов
![]() ,
входящих в разложение
,
входящих в разложение
![]() (7). Зададимся величиной
(7). Зададимся величиной
![]() ,
пока неизвестной, умножим (7) на
,
пока неизвестной, умножим (7) на
![]() и почленно вычислим из (6),получаем
и почленно вычислим из (6),получаем
![]()
![]()
вектор
![]() является планом, если его компоненты
положительны.
является планом, если его компоненты
положительны.
![]() (9).
(9).
Из (9) следует, что
![]() ,
план, если
,
план, если
![]() (10).
(10).
Чтобы план был опорным должно быть m - положительных компонентов.
Необходимо обратить в нуль хотя бы одну из компонентов
![]() (11).
(11).
3.8. Условия оптимальности
Предположим, что задача линейного
программирования (1) - (3) обладает планами
и каждый ее опорный план невырожден. В
этом случае для опорного плана (5) имеем
![]() (12)
(12)
![]() (13), где
(13), где
![]() - это значение линейной формы,
соответствующее плану
- это значение линейной формы,
соответствующее плану
![]() .
Разложение любого вектора
.
Разложение любого вектора
![]() по векторам базиса
по векторам базиса
![]() - единственно.
- единственно.
![]() (14)
(14)![]()
![]() (15)
(15)
Теорема (для задачи на min):
Если для некоторого вектора
выполняются условия
![]() ,
то план
,
то план
![]() не является оптимальным и можно построить
такой план X:
не является оптимальным и можно построить
такой план X:
![]() .
.
Доказательство:
Умножим равенство (14) на
![]() и вычтем из равенства (12), получаем
и вычтем из равенства (12), получаем
![]() .
.
Умножим равенство (15) на и вычтем из равенства (13), получаем
![]()
![]() (16).
(16).
Следствие: Если для некоторого плана
разложение всех векторов
![]() в данном базисе, удовлетворяющих условию
в данном базисе, удовлетворяющих условию
![]() (17),
то план
является оптимальным. Неравенство (17)
это условие оптимальности задачи на
минимум, а величины
(17),
то план
является оптимальным. Неравенство (17)
это условие оптимальности задачи на
минимум, а величины
![]() - оценки плана.
- оценки плана.
Теорема (для задачи на max):
Если для некоторого вектора
выполняются условия
,
то план
не является оптимальным и можно построить
такой план X:
![]() .
.
Следствие: Если для некоторого плана
разложение всех векторов
в данном базисе, удовлетворяющих условию
![]() (18),
то план
является оптимальным. Неравенство (18)
это условие оптимальности задачи на
минимум, а величины
- оценки плана.
(18),
то план
является оптимальным. Неравенство (18)
это условие оптимальности задачи на
минимум, а величины
- оценки плана.
![]() - формула Жордана-Гаусса.
- формула Жордана-Гаусса.
![]()
