
- •Учебно-методические материалы к изучению дисциплины «Методы оптимизации» (конспект лекций)
- •1. Классификация задач оптимизации
- •2. Классификация математических методов и моделей в экономике
- •3. Линейное программирование
- •3.1. Постановка задачи линейного программирования
- •3.2. Экономическая интерпретация задач линейного программирования
- •3.3. Требования совместности условий
- •3.4. Графический метод решения задач линейного программирования
- •3.5. Симплекс-метод
- •3.6. Модифицированный симплекс-метод
- •3.7. Построение опорных планов
- •3.8. Условия оптимальности
- •3.9. Метод искусственного базиса
- •3.10. Транспортная задача
- •3.11. Двойственные задачи линейного программирования
- •3.12. Устойчивость оптимизационного решения
- •4. Нелинейное программирование
- •4.1. Классификация и общая постановка задач нелинейного программирования
- •4.2. Метод множителей Лагранжа
- •4.3. Возможные обобщения метода множителей. Седловая точка функции Лагранжа
- •4.4. Оптимальные решения при ограничениях-неравенствах. Теорема Куна - Таккера
- •4.5. Выпуклое программирование. Задача выпуклого программирования
- •4.6. Квадратичное программирование
- •4.7. Градиентные методы
- •5. Оптимизация на графах
- •5.1. Основные понятия теории графов
- •5.2. Связность
- •5.3. Подграфы
- •5.4. Матрица графов
- •5.5. Потоки в сетях
- •5.6. Задача о максимальном потоке сети
- •5.7. Задача о кратчайшем пути
- •5.8. Задача коммивояжера
- •5.9. Оптимизация сетевого графика
- •5.10. Методы оптимизации производственной программы
- •6. Динамическое программирование
- •6.1. Общая постановка задачи динамического программирования
- •6.2. Принцип оптимальности. Уравнение Беллмана
- •6.3. Простейшие экономические задачи, решаемые методом динамического программирования
- •7. Математические модели потребительского поведения и спроса
- •7.1. Отношение предпочтения и функция полезности
- •7.2. Решение задачи об оптимальном выборе потребителя
- •7.3. Функции спроса. Коэффициент эластичности
5.7. Задача о кратчайшем пути
Частным случаем задачи об
оптимальном потоке является задача
построения кратчайшего пути между
двумя вершинами пути. Пусть дан граф
G=[N,
A]
, каждой дуге которого поставлено в
соответствие число С(х,
у), называемое длиной
дуги (х, у). Выделяются
две вершины графа - s
и t
. Требуется найти путь наименьшей длины,
ведущий из вершины s
в вершину t.
При этом длина
произвольного пути
![]() определяется следующим
образом:
определяется следующим
образом:
![]() .
.
Данная задача может быть сформулирована как задача об оптимальном потоке. Ставится задача определения потока, минимизирующего функционал
![]() ,
где
,
где
![]() .
.
Рассмотрим теперь сеть,
вершина s
которой является
источником единичной интенсивности,
t
- стоком единичной
интенсивности, остальные вершины -
нейтральные. Дугам приписываются
неограниченные пропускные способности,
а стоимость перевозок по дуге полагается
равной длине дуги. Для потока
![]() в рассматриваемой сети
в рассматриваемой сети
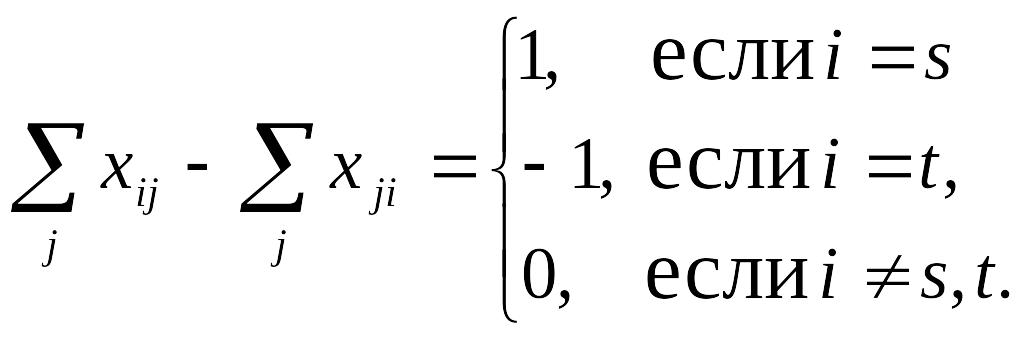
Пусть имеется некоторый
конечный граф G
= [N
={1,2,…,n},
а],
каждой вершине
i
которого поставлено в соответствие
некоторое число
![]() ,
называемое
интенсивностью потока.
Вершины назовем
источниками, нейтральными вершинами
и стоками, если
,
называемое
интенсивностью потока.
Вершины назовем
источниками, нейтральными вершинами
и стоками, если
![]() ,
,
![]() и
и
![]() соответственно. Потоком
в полученной сети
назовем совокупность величин
соответственно. Потоком
в полученной сети
назовем совокупность величин
![]() ,
удовлетворяющих соотношениям
,
удовлетворяющих соотношениям
![]() ,
,
![]() .
.
5.8. Задача коммивояжера
Пример. Пусть имеются пять пунктов, соединенных между собой дорогами так, что из любого пункта можно проехать в любой другой пункт (рис. 11). Известно время перевозки из пункта i в пункт j (табл. 17).
Таблица 17
Из пункта i |
В пункт j |
||||
1 |
2 |
3 |
4 |
5 |
|
1 |
0 |
10 |
25 |
25 |
10 |
2 |
1 |
0 |
10 |
15 |
2 |
3 |
8 |
9 |
0 |
20 |
10 |
4 |
14 |
10 |
24 |
0 |
15 |
5 |
10 |
8 |
25 |
27 |
0 |
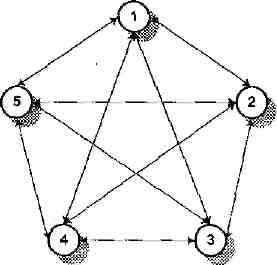
Рис. 11
Требуется найти такой маршрут, начинающийся в данном пункте, проходящий через все пункты и заканчивающийся в пункте выезда, чтобы его продолжительность была наименьшей.
Решение. Для решения этой задачи
необходимо составить математическую
модель. Введем обозначения: i
и j; - номера пунктов выезда
и въезда; tij - время
переезда из пункта i
в пункт j. Из табл. 17
видно, что tij в
общем случае может быть не равно времени
переезда в обратном направлении
![]() (например, когда один пункт на вершине
горы, а другой - у ее подножия). Введем
булевы переменные:
(например, когда один пункт на вершине
горы, а другой - у ее подножия). Введем
булевы переменные:
![]()
Составим модель (рис. 12).
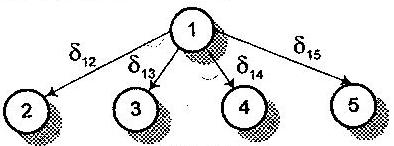
Рис. 12
Из п. 1 можно выехать в любой из п. 2 или 5, или 3, или 4, или остаться в п. 1. Но при этом можно выехать только в одном единственном направлении. Это условие можно записать так:
![]() или
или

Эти зависимости обеспечивают выполнение условия, что из каждого пункта выезд производится только один раз и только в одном направлении.
Условие въезда в п. 1 аналогично условию выезда из п. 1 (рис. 12). Требование минимальной продолжительности маршрута запишется в виде целевой функции:
![]()
где tij берутся из исходной таблицы, а δij - искомые переменные.
Тогда всю задачу можно сформулировать:
![]()

В результате решения системы (*) получим
(рис. 13) следующие значения
![]() остальные
остальные
![]()
![]()
Переходя от частной к общей постановке, задачу коммивояжера можно сформулировать как:
![]()
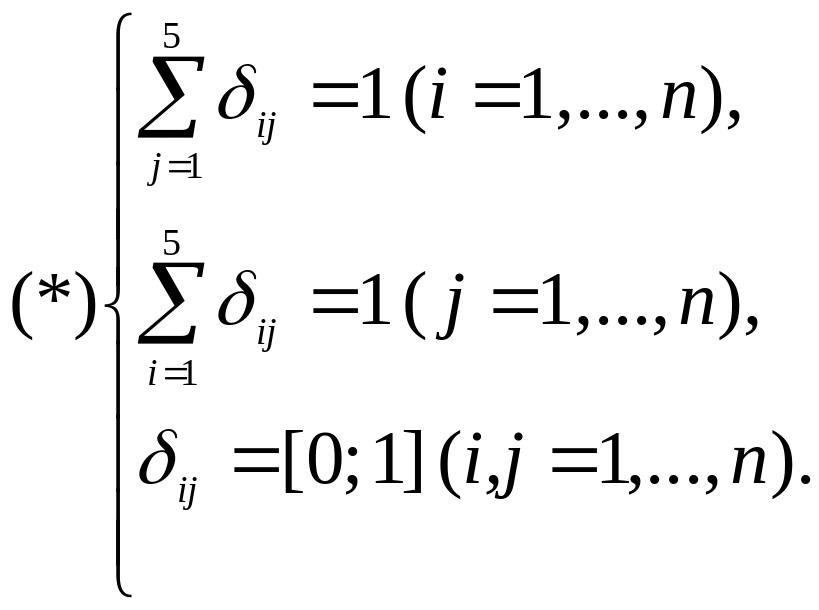
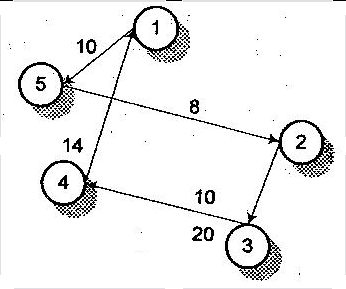
Рис. 13
