4.5. Выпуклое программирование. Задача выпуклого программирования

Определение: Функция , заданная на выпуклом множестве X, называется выпуклой, если для любых двух точек и из X и любо­го выполняется соотношение

(4)

Определение: Функция , заданная на выпуклом множестве X, называется вогнутой, если для любых двух точек и из X и любо­го выполняется соотношение

(5)

Если неравенства (4) и (5) считать строгими и они выполняются при , то функция является строго выпуклой (строго вогнутой). Выпуклость и вогнутость функций определяется только относительно выпуклых множеств.

Если , где , - выпуклые (вогнутые) функции на некотором выпуклом множестве , то функция f(x) - также выпуклая (вогнутая) на X.

Основные свойства выпуклых и вогнутых функций:

1. Множество точек минимума выпуклой функции, заданной на выпук­лом множестве, - выпукло.

2. Пусть f(x) - выпуклая функция, заданная на замкнутом выпуклом множестве . Тогда локальный минимум f(x) на X является и глобальным.

3. Если глобальный минимум достигается в двух различных точках, то он достигается и в любой точке отрезка, соединяющего данные точки.

4. Если - строго выпуклая функция, то ее глобальный минимум на выпуклом множестве X достигается в единственной точке.

5. Пусть функция f(x) - выпуклая функция, заданная на выпуклом множестве X, и, кроме того, она непрерывна вместе со своими частными производными первого порядка во всех внутренних точках X. Пусть - точка, в которой . Тогда в точке достигается локальный минимум, совпадающий с глобальным минимумом.

6. Множество точек глобальных (следовательно, и локальных) мини­мумов выпуклой функции , заданной на ограниченном замкнутом вы­пуклом множестве X, включает хотя бы одну крайнюю точку; если множест­во локальных минимумов включает в себя хотя бы одну внутреннюю точку множества X, то является функцией-константой.

Рассмотрим задачу нелинейного программирования

(6)

при ограничениях

, (7)

. (8)

Для решения сформулированной задачи в такой общей постановке не существует универсальных методов. Однако для отдельных классов задач, в которых сделаны дополнительные ограничения относительно свойств функ­ций f(x) и , разработаны эффективные методы их решения.

Говорят, что множество допустимых решений задачи (6) - (8) удов­летворяет условию регулярности, или условию Слейтера, если существует, по крайней мере, одна точка , принадлежащая области допустимых ре­шений такая, что . Задача (6) - (8) называется задачей выпуклого программирования, если функция является во­гнутой (выпуклой), а функции - выпуклыми. Функцией Лагранжа задачи выпуклого программирования (6) - (8) называется функция

,

где - множители Лагранжа.

Точка называется седловой точкой функции Лагранжа, если

для всех и .

Теорема (Куна - Таккера): Для задачи выпуклого програм­мирования (6) - (8), множество допустимых решений которой обладает свойством регулярности, является опти­мальным решением тогда и только тогда, когда существует такой вектор , что - седловая точка функции Лагранжа.

Если предположить, что функции f и непрерывно дифференци­руемы, то теорема Куна - Таккера может быть дополнена аналитическими выражениями, определяющими необходимые и достаточные условия того, чтобы точка была седловой точкой функции Лагранжа, т. е. являлась решением задачи выпуклого программирования:

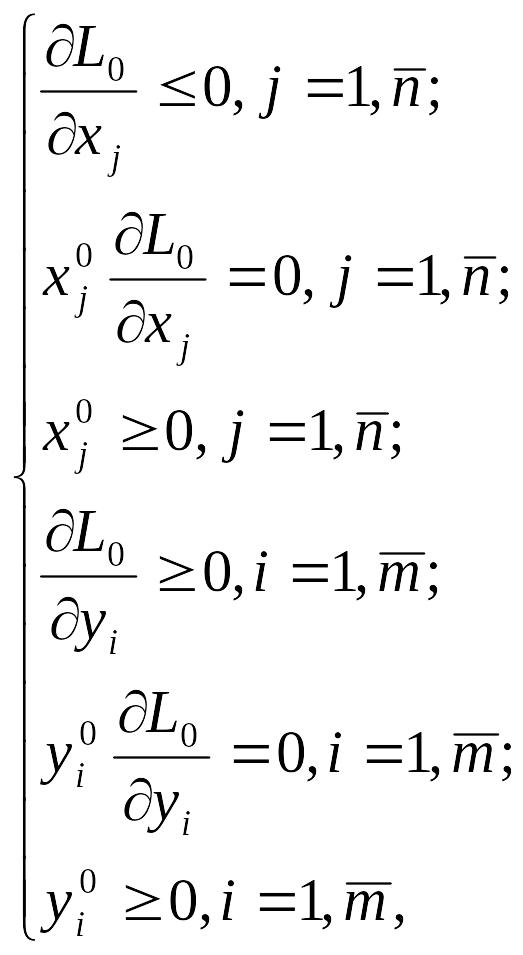
где и значения соответствующих частных производных функции Лагранжа, вычисленных в седловой точке.