
- •Учебно-методические материалы к изучению дисциплины «Методы оптимизации» (конспект лекций)
- •1. Классификация задач оптимизации
- •2. Классификация математических методов и моделей в экономике
- •3. Линейное программирование
- •3.1. Постановка задачи линейного программирования
- •3.2. Экономическая интерпретация задач линейного программирования
- •3.3. Требования совместности условий
- •3.4. Графический метод решения задач линейного программирования
- •3.5. Симплекс-метод
- •3.6. Модифицированный симплекс-метод
- •3.7. Построение опорных планов
- •3.8. Условия оптимальности
- •3.9. Метод искусственного базиса
- •3.10. Транспортная задача
- •3.11. Двойственные задачи линейного программирования
- •3.12. Устойчивость оптимизационного решения
- •4. Нелинейное программирование
- •4.1. Классификация и общая постановка задач нелинейного программирования
- •4.2. Метод множителей Лагранжа
- •4.3. Возможные обобщения метода множителей. Седловая точка функции Лагранжа
- •4.4. Оптимальные решения при ограничениях-неравенствах. Теорема Куна - Таккера
- •4.5. Выпуклое программирование. Задача выпуклого программирования
- •4.6. Квадратичное программирование
- •4.7. Градиентные методы
- •5. Оптимизация на графах
- •5.1. Основные понятия теории графов
- •5.2. Связность
- •5.3. Подграфы
- •5.4. Матрица графов
- •5.5. Потоки в сетях
- •5.6. Задача о максимальном потоке сети
- •5.7. Задача о кратчайшем пути
- •5.8. Задача коммивояжера
- •5.9. Оптимизация сетевого графика
- •5.10. Методы оптимизации производственной программы
- •6. Динамическое программирование
- •6.1. Общая постановка задачи динамического программирования
- •6.2. Принцип оптимальности. Уравнение Беллмана
- •6.3. Простейшие экономические задачи, решаемые методом динамического программирования
- •7. Математические модели потребительского поведения и спроса
- •7.1. Отношение предпочтения и функция полезности
- •7.2. Решение задачи об оптимальном выборе потребителя
- •7.3. Функции спроса. Коэффициент эластичности
4.4. Оптимальные решения при ограничениях-неравенствах. Теорема Куна - Таккера
Изученные особенности функции позволяют сформулировать положения, относящиеся непосредственно к нелинейным, задачам математического программирования. Пусть дана задача: найти
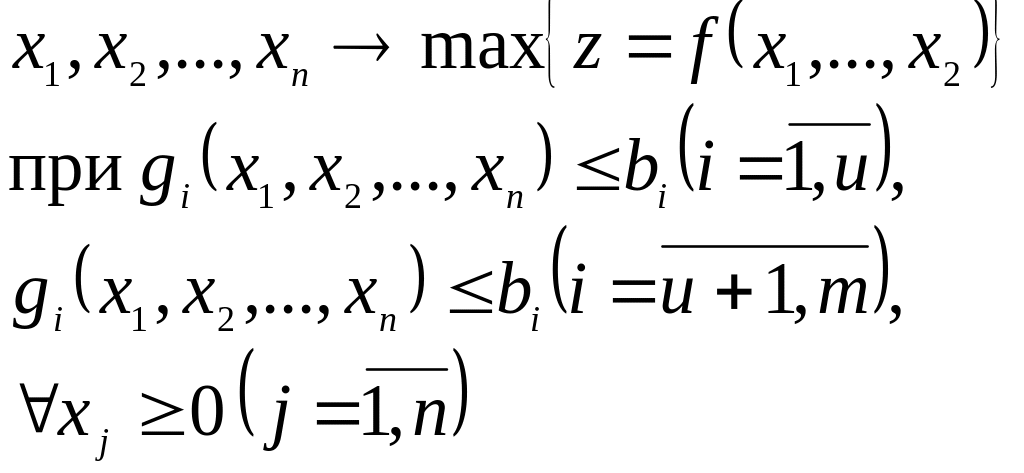 (1)
(1)
Все предположения относительно z
и gi
![]() ,
выдвинутые выше,
сохраняются здесь полностью. Требуется
получить условия
существования решений, основанные на
введенных понятиях.
,
выдвинутые выше,
сохраняются здесь полностью. Требуется
получить условия
существования решений, основанные на
введенных понятиях.
Чтобы избежать неудобств, связанных с присутствием в (1) ограничений-неравенств и требований неотрицательноcти переменных xj, представим (1) в эквивалентной форме
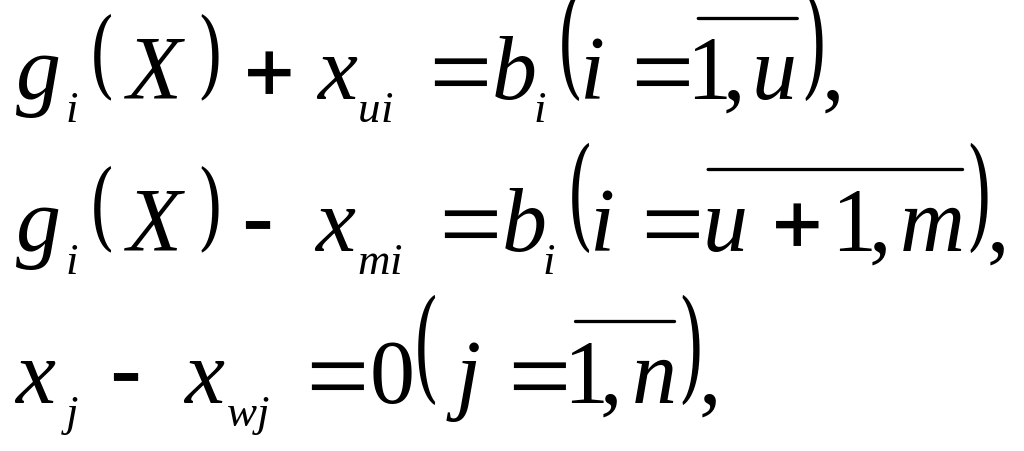 (2)
(2)
где
![]() - вспомогательные переменные, позволяющие
формально исключить знаки «≤, ≥» (1).
Для этого случая, функция Лагранжа
запишется как
- вспомогательные переменные, позволяющие
формально исключить знаки «≤, ≥» (1).
Для этого случая, функция Лагранжа
запишется как
![]()
а необходимые
условия, которым должны удовлетворять
оптимальные
![]() ,
принимают обычный вид
,
принимают обычный вид
![]()
Рассмотрим более подробно равенства
![]()
Их можно представить как
![]() (3)
(3)
собрав под знаком
Σ производные по хj
первых, двух
сумм выражения
![]() .
Ясно, что появление здесь слагаемого
.
Ясно, что появление здесь слагаемого
![]() есть следствие перехода от системы (1)
к (2). Обратим
теперь .внимание на то, что в левую часть
(3) входит
выражение производной по хj.
Функции
есть следствие перехода от системы (1)
к (2). Обратим
теперь .внимание на то, что в левую часть
(3) входит
выражение производной по хj.
Функции
![]()
т.е. функции Лагранжа в ее классическом виде. Для cоставления достаточно данных исходной задачи (1), поэтому естественно стремиться сформулировать такие условия существования экстремума f(X), которые включали бы только , а не .
Обратим внимание
на множитель
,
связанный с
j-й
искусственной строкой (2) и обладающий
свойством
![]() .
При
.
При
![]() (или, что то же, при
(или, что то же, при
![]() )
он обращается в
нуль, и необходимые условия существования
Х0
(из
рассматриваемых в данный момент)
принимают вид
)
он обращается в
нуль, и необходимые условия существования
Х0
(из
рассматриваемых в данный момент)
принимают вид
![]()
Далее, при
![]() (это равносильно равенству
(это равносильно равенству
![]() ,
так как
,
так как
![]() )
соответствующий множитель
отличен, вообще
говоря, от нуля. Его знак в этом случае
определяется
из следующих соображений: если правой,
части любой
строки
)
соответствующий множитель
отличен, вообще
говоря, от нуля. Его знак в этом случае
определяется
из следующих соображений: если правой,
части любой
строки
![]() дать отрицательное приращение,
то область определения исследуемой
задачи только
расширится (произвольное значение
дать отрицательное приращение,
то область определения исследуемой
задачи только
расширится (произвольное значение
![]() удовлетворяет
и неравенству
удовлетворяет
и неравенству
![]() );
величина z0
при этом не
уменьшится (всякое расширение U,
создает предпосылки для улучшения
ожидаемых z0),
т.е.
);
величина z0
при этом не
уменьшится (всякое расширение U,
создает предпосылки для улучшения
ожидаемых z0),
т.е.
![]() или
или
![]() .
Таким образом, при
необходимые
условия есть
.
Таким образом, при
необходимые
условия есть
![]()
Обращаясь теперь
к группе соотношений
![]() и применяя те
же способы оценки знаков
и применяя те
же способы оценки знаков
![]() ,
можно получить, объединенную сводку
искомых необходимых
условий, которым должны удовлетворять
оптимальные
,
можно получить, объединенную сводку
искомых необходимых
условий, которым должны удовлетворять
оптимальные
![]() в рассматриваемой задаче (1):
в рассматриваемой задаче (1):
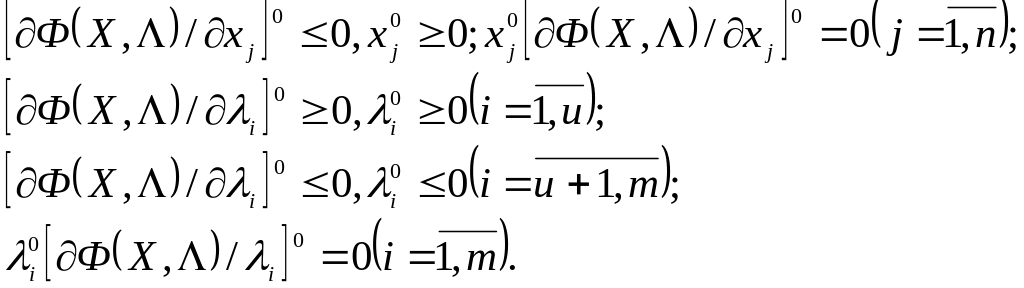 (4)
(4)
Следует специально
подчеркнуть, что соотношения (4)
должны рассматриваться лишь тогда,
когда существуют такие
![]() ,
при которых
,
при которых
![]() ,
т.е.
,
т.е.
![]() ;
в противном случае
возникает неопределенность выбора
;
в противном случае
возникает неопределенность выбора
![]() (нарушается условие регулярности
ограничений (1), множество компонент
становится неограниченным), и равенства
(нарушается условие регулярности
ограничений (1), множество компонент
становится неограниченным), и равенства
![]() теряют смысл.
теряют смысл.
Очевидно, требования (4) полностью совпадают с (1) (п. 4.3) при Х≥0, причем соответствие результатов распространяется и на достаточные условия существования .
Пусть точка
удовлетворяющая
(4), является седловой
для
![]() ;
следовательно, должно выполняться
неравенство
;
следовательно, должно выполняться
неравенство
![]()
В силу (4) сумма
![]() равна нулю, а каждое
слагаемое суммы
равна нулю, а каждое
слагаемое суммы
![]() неотрицательно поскольку знаки разностей
неотрицательно поскольку знаки разностей
![]() в (1) и соответствующих
в (1) и соответствующих
![]() в (4) всегда совпадают. Таким образом,
приходим к
утверждению «f(X)
+ (неотрицательная величина)
≤ f(X0)»
и тем более
в (4) всегда совпадают. Таким образом,
приходим к
утверждению «f(X)
+ (неотрицательная величина)
≤ f(X0)»
и тем более
![]() .
Этим подтверждается
достаточность исходного предположения.
.
Этим подтверждается
достаточность исходного предположения.
Проведенный анализ
свойств экстремума z
в задаче (1)
позволяет дать краткую формулировку
теоремы
Куна - Таккера:
для того, чтобы
экстремум функции f(X)
был достигнут
в точке
![]() при условиях
(1), необходимо и достаточно требовать
существования
таких
при условиях
(1), необходимо и достаточно требовать
существования
таких
![]() ,
при которых
является седловой точкой функции
,
при которых
является седловой точкой функции
![]() .
.
Заметим теперь, что теорема Куна - Таккера, отражающая роль седловой точки , может рассматриваться с более общих позиций, вне связи с предположениями о дифференцируемости .
Пусть, например, в
задаче (1) отсутствуют требования,
существования производных
![]() и некоторая
точка
и некоторая
точка
![]() является седловой для функции
является седловой для функции
![]()
на множестве U,
причем
![]() .
Нетрудно убедиться, что эти условия
являются
достаточными условиями экстремума, (в
данном случае максимума).
Действительно, из определения седловой
точки следует
.
Нетрудно убедиться, что эти условия
являются
достаточными условиями экстремума, (в
данном случае максимума).
Действительно, из определения седловой
точки следует
![]() ;
;
правое неравенство есть
![]() или
или
![]() ;
;
поскольку знаки
![]() ,
совпадают со знаками соответствующих
разностей
,
совпадают со знаками соответствующих
разностей
![]() ,
и кроме того, рассматриваемое
неравенство выполняется для всех
допустимых
,
и кроме того, рассматриваемое
неравенство выполняется для всех
допустимых
![]() (в частности, для
(в частности, для
![]() ),
получаем
),
получаем
![]() ;
в этой ситуации левое неравенство
принимает вид f(X)
+ (неотрицательная величина) ≤ f(Х*)
или f(X)
≤ f(Х*),
что и подтверждает оптимальность
X*.
;
в этой ситуации левое неравенство
принимает вид f(X)
+ (неотрицательная величина) ≤ f(Х*)
или f(X)
≤ f(Х*),
что и подтверждает оптимальность
X*.
Таким образом, использование производных функции в ходе доказательств теорем о существований экстремума совсем не обязательно, однако в инженерных задачах оно часто приводит к упрощениям расчетов.
В заключение полезно
подвести некоторые итоги: исследована
проблема обобщения классического
метода множителей
Лагранжа на случай ограничений вида
![]() и Х≥0
в задачах
нелинейного программирования;
показана возможность такого обобщения
и изучены
особенности функции Лагранжа
в точке относительного
экстремума f(X);
установлена связь между
условиями существования точек X0
и
,
выраженная
теоремой Куна - Таккера. Ниже дан пример
•непосредственного
использования полученных результатов.
и Х≥0
в задачах
нелинейного программирования;
показана возможность такого обобщения
и изучены
особенности функции Лагранжа
в точке относительного
экстремума f(X);
установлена связь между
условиями существования точек X0
и
,
выраженная
теоремой Куна - Таккера. Ниже дан пример
•непосредственного
использования полученных результатов.
Пример. Найти
![]()
при
![]()
Решение. Составим функцию Лагранжа в ее классическом виде (так, как это было бы в случае ограничений-равенств отсутствия требований неотрицательности х1, х2):
![]()
Из условий
![]() и
и
![]() получаем
получаем
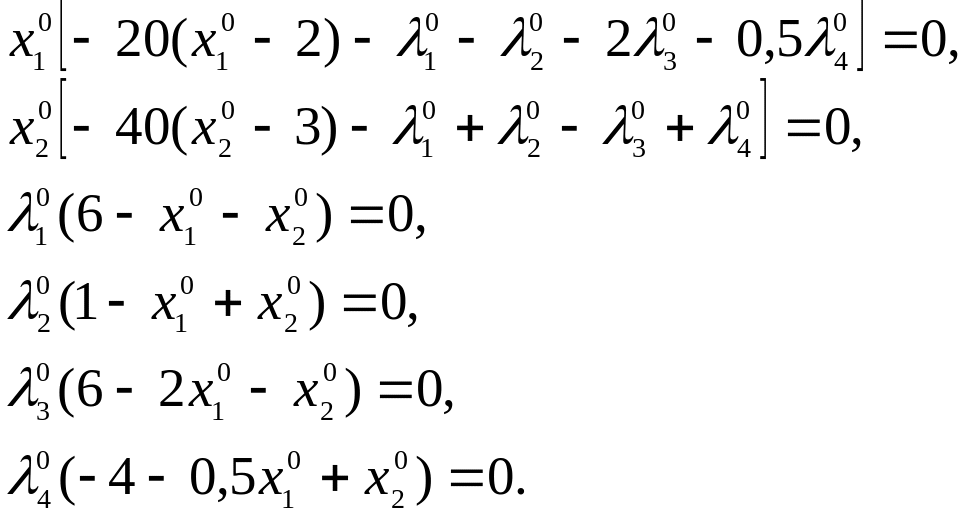
Среди возможных решений этой системы нужно выбрать теперь те, которые удовлетворяют соотношениям (4). Оказывается, этим свойством обладает одно решение:
![]()
тот факт, что все
оказались равными нулю,
а
![]() ,
указывает на несущественность исходных
ограничений задачи;
проверка достаточных условий сводится
к установлению факта выпуклости
z
(это можно сделать здесь простыми
геометрическими построениями).
,
указывает на несущественность исходных
ограничений задачи;
проверка достаточных условий сводится
к установлению факта выпуклости
z
(это можно сделать здесь простыми
геометрическими построениями).
Теория Куна - Таккера позволяет заметно расширить круг задач нелинейного программирования, решение которых может быть получено в аналитическом виде.
