40

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Факультет информационных технологий и робототехники

Кафедра программного обеспечения вычислительной техники

и автоматизированных систем

Профессор р.И.Фурунжиев

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

по курсу:

"ОПТИМИЗАЦИЯ ПРОЕКТИРОВАНИЯ

ТЕХНИЧЕСКИХ СИСТЕМ НА ЭВМ"

Минск - 2006

СОДЕРЖАНИЕ

	Стр.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ
Работа 1. Разработка математических моделей и анализ динамики оптимизируемых систем.
Работа 2. Моделирование внешней среды.
Работа 3. Статистический анализ качества систем методом Монте- Карло.
Работа 4. Оптимальное проектирование конечномерных систем (параметрическая оптимизация).
Работа 5. Оптимальное проектирование бесконечномерных систем (систем управления).
ЛИТЕРАТУРА
ПРИЛОЖЕНИЯ Примеры копий экранов Образец титульного листа

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ

В соответствии с календарным планом дисциплины "Оптимизация проектирования технических систем на ЭВМ" предусмотрено выполнение следующих лабораторных работ.

№№ работ	Темы лабораторных работ	Часов (план)
1.	Разработка математических моделей и анализ динамики оптимизируемых систем.	8
2.	Моделирование внешней среды.	8
3.	Статистический анализ качества систем методом Монте-Карло.	4
4.	Оптимальное проектирование конечномерных систем (параметрическая оптимизация).	8
5.	Оптимальное проектирование бесконечномерных систем (систем управления).	8
	Всего:	36

Все лабораторные работы предусматривают изучение методов оптимального проектирования, разработку алгоритмов, программ и компьютерное моделирование. По каждой работе вычисления необходимо оформить в виде отдельных UNIT: Runge, Perturb, Monte-Сarlo, Optim, Contrl), не использующих формы. Затем эти UNIT используются в последующих работах.

Для всех работ необходимо:

1. Сформулировать цель работы.

2. Привести общую формулировку задачи.

2. Разработать математическую модель.

3. Выбрать метод и разработать алгоритм решения.

4. Разработать приложение и подготовить его к поставке.

5. Произвести компьютерное моделирование, используя созданное приложение на Delphi, с построением соответствующих таблиц и графиков.

6. Сделать выводы и обобщения.

7. Составить отчет.

Отчеты по всем лабораторным работам рекомендуется объединить в общий отчет. Перед печатанием электронный вариант отчета показать преподавателю для внесения коррекции.

При выполнении работ рекомендуется изучить соответствующие разделы учебного пособия [1]:

главу 9 - для выполнения работы 1;

главу 10 – для выполнения работ 2 и 3;

главу 11 - для выполнения работы 4.

Для выполнения работы 5 рекомендуется изучить соответствующий раздел конспекта либо работу [6].

Работа 1.

Разработка математических моделей

и анализ динамики оптимизируемых систем

Известные общие подходы к созданию математических моделей. Для многих динамических систем можно выделить фрагмент в виде двухмассовой колебательной системы, расчетная схема которой приведена на фиг.1.

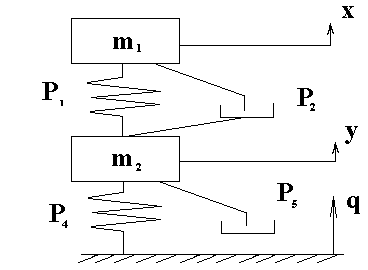
Фиг.1. Расчетная схема двухмассовой колебательной системы

Система находится в равновесии, поэтому

Рассматривая колебания системы относительно положения статического равновесия, в соответствии со вторым законом Ньютона для фазовых координат (либои) можно записать:

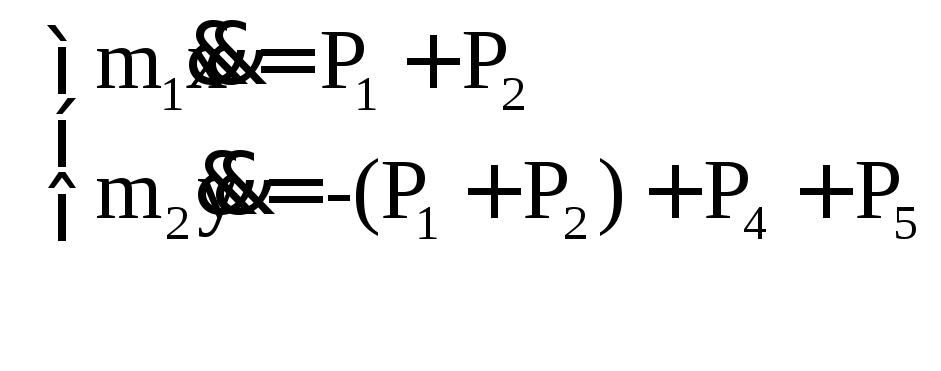. (1)

Начальные условия:

Здесь силы, действующие на массы как показано на расчетной схеме.

Пусть упругие силы пропорциональны деформациям, а диссипативные силы – скоростям соответствующих деформаций:

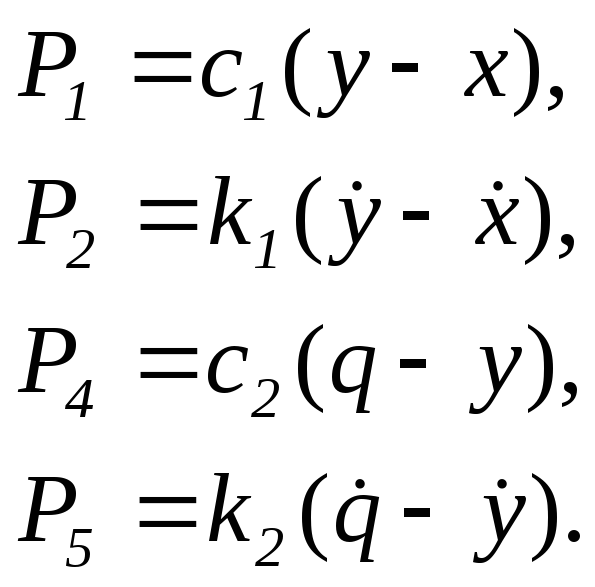
Тогда система (1) примет вид:

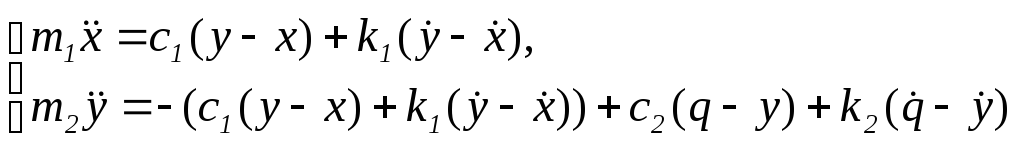
или

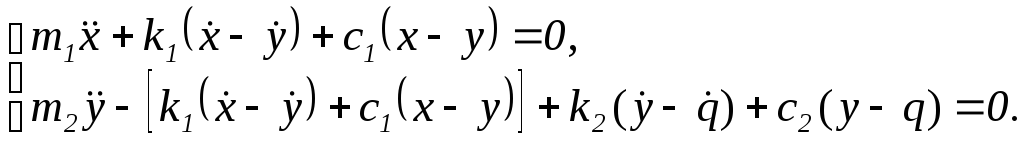
Введем следующие обозначения:

Тогда систему уравнений (1) можно записать в виде:

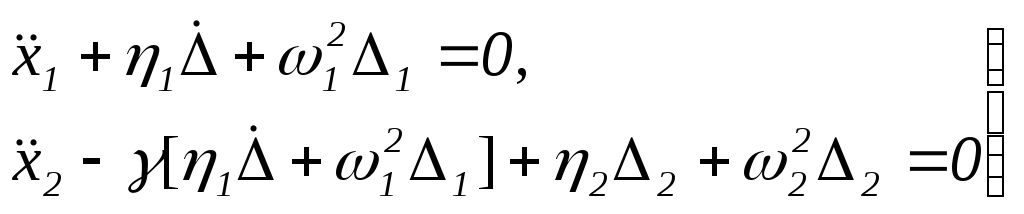, (2)

где константы определяют частотные свойства системы, а константы диссипативные.

Для численного интегрирования методом Рунге-Кутта четвертого порядка система (2) заменой переменных приводится к системе дифференциальных уравнений первого порядка [1, с.311].

Детерминированное (гармоническое) возмущение q(t) рекомендуется оформить в виде процедуры-функции:

Function q : Extended;

begin

q := q0 * sin(omega_q * t);

end;

а производную возмущения Dq(t) - в виде процедуры-функции:

Function Dq : Extended;

begin

Dq := q0 * omega_q * cos(omega_q * t);

end;

Здесь q0 и omega_q – амплитуда и частота гармонического возмущения соответственно.

Вычисление правых частей системы рекомендуется оформить в виде процедуры:

Procedure Deriv(x:Vector; var Dx:Vector);

begin

Dx[1] := x[2];

Dx[2] :=-eta1*(x[2]-x[4])-sqr(omega1)*(x[1]-x[3]);

Dx[3] := x[4];

Dx[4] := gamma*(eta1*(x[2]-x[4])+sqr(omega1)*(x[1]-

x[3])) -eta2*(x[4]-Dq)-sqr(omega2)*(x[3]-q);

end;