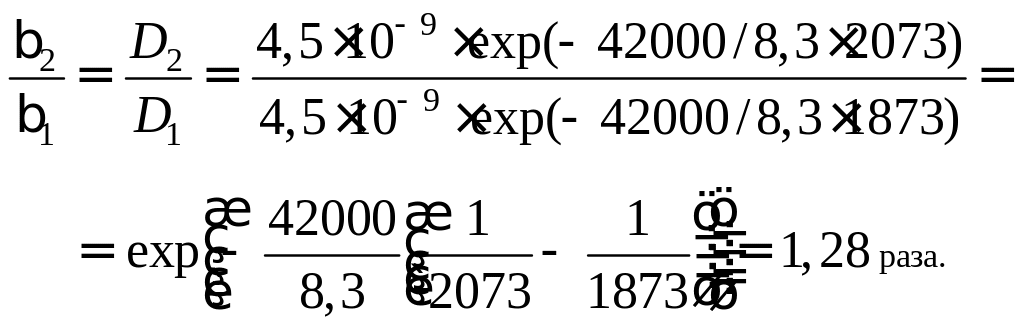3. Рафинирование расплавов от примесей

Синтетические шлаки применяют для рафинирования расплавов от вредных примесей. Например, чугуна и стали от серы. Установлено также, что при этом происходит уменьшение содержания растворенных газов. Скорость перехода примесей из металла в шлак описывается уравнением:

, (1.10)

где – коэффициент массопереноса; С_Р – равновесное содержание примесного элемента в металле, %.

Соотношение содержаний примесного элемента, в металле (С_Ме) и шлаке (С_Ш), называется коэффициентом распределения:

.

Например, коэффициент распределения серы между «белым шлаком» электродуговой печи и сталью составляет примерно 150 (К = 150).

После интегрирования (1.10) имеем:

, (1.11)

Равновесное содержание примеси можно определить по балансовому уравнению:

, (1.12)

где М_Ш – массовая доля шлака.

Коэффициент массопереноса определяется:

, (1.13)

где D – коэффициент диффузии примеси в металле, м²/с; – толщина диффузионного слоя, м.

Толщину диффузионного слоя точно определить или рассчитать довольно трудно, т.к. она зависит от интенсивности потоков, перемешивающих металл.

Коэффициент массопереноса можно оценить с достаточной точностью по уравнению:

, (1.14)

где – кинематическая вязкость металла, м²/с; U_М – скорость перемешивания металла, м/с; R_К – радиус ковша с металлом, м.

4. Решение типовых задач

1. Каким поверхностным натяжением должен обладать шлак, абсолютно смачивающий включения TiO₂ , чтобы оксиды титана самопроизвольно переходили из жидкой стали (железа) в шлак? Необходимые данные для расчета приведены в табл. 1.1.

Ответ: >185 МДж/м².

Решение. Для самопроизвольного перехода включений из металла в шлак изменение удельной свободной энергии системы ΔG / S_В должно быть меньше нуля. Согласно уравнения (1.2) должно выполняться соотношение

,

МДж/м².

2. Через какое время произойдёт уменьшение концентрации включений Al₂O₃ размером более 200 мкм в стали в два раза при выстаивании её под слоем синтетического шлака?

Плотность стали в жидком состоянии . Плотность включений . Динамическая вязкость стали Диаметр ковша – 1 м, высота металла в ковше – 1 м. Конвективными потоками в металле пренебречь.

Ответ: через 22,9 часа.

Решение. Для нахождения времени выстаивания металла применим уравнение (1.8). Скорость всплывания включений найдем по формуле Стокса:

^, (1.15)

где U_B – скорость всплывания включений, м/с; – радиус включе ний, м.

Примем согласно условию минимальный радиус включений r = 100мкм = 10^-4м; – динамическая вязкость металла, .

Содержание включений по условию должно снизиться в 2 раза. Тогда в уравнении (1.8) отношение С / С₀ = 0,5 . Подставим известные значения в это уравнение и прологарифмируем его:

;

Отсюда находим время всплывания включений

.

3. Как изменится скорость десульфурации стали шлаком, если её температура возрастет с 1600 до 1800 °С? Равновесное содержание серы в стали и толщине диффузионного слоя не меняются. Температурная зависимость коэффициента диффузии серы в железе имеет вид:

, м/с.

Ответ: скорость десульфурации возрастет в 1,28 раза.

Решение. Известно, что удаление серы в шлак происходит диффузионным путем. При этом в металле на границе со шлаком создается тонкий неперемешиваемый диффузионный слой. Скорость перехода серы через этот слой определяется по уравнению (1.10). Так как коэффициенты диффузии пропорциональны коэффициентам массопереноса и оба зависят от температуры, то соотношение этих коэффициентов при Т₁ и Т₂ и будет увеличением скорости десульфурации. Тогда, за счет увеличения температуры скорость десульфурации возрастет в :