2.1 Пояснения и применяемые обозначения в алгоритме.
Массивы и переменные:
C[n][n] – массив размерностьюnнаn. Массив стоимостей ребер в графе.
c[i][j] – элемент массива C[n][n], соответствующийi-той строке иj-ому столбцу.
Length[n] - массив стоимостей текущего пути.
Road[n] - массив номеров вершин текущего пути.
Tail - номер вершины в которую проведено ребро.
Head - номер первой вершины.
Summ - длинна текущего пути.
Функции используемые в блок схемах:
Keyboard Input () – организация ввода с клавиатуры.
Open Document () – открытие документа.
Search Minimal Vertex () – поиск минимального значения в массиве C[n][n].
Infinity (C[][]) – присвоение бесконечной стоимостей рассмотренным вершинам.
Plus (C[][]) – операция аналогичная i = i + 1, только с проверкой условия: если i = n – 1 , то i = 0 пока i не равно Head-1
Summ (Length[], Summ) – подсчет суммы всех элементов массива Length[n] , а затем к результату прибавляет значение c[Head][Tail].
Обозначения:
= = - сравнение (равно)
! = - неравно
switch– выбор условия, эквивалентен нескольким инструкциямif(Если).
2.2 Блок-схема к Жадному алгоритму.
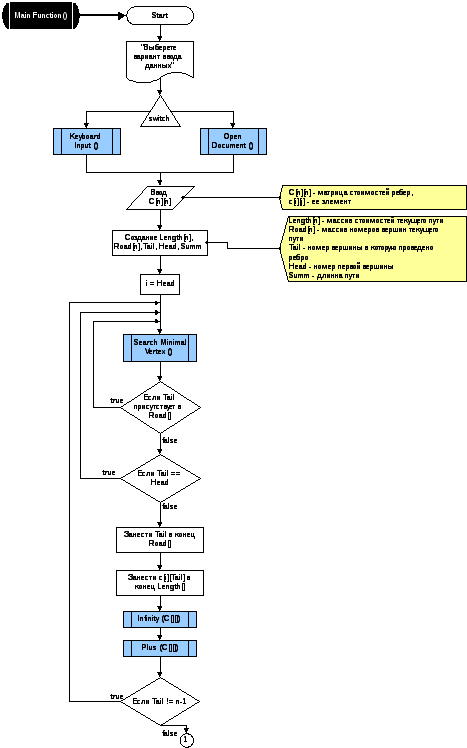
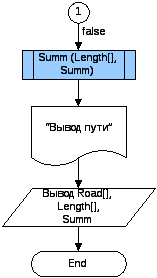
3.1. Образец тестирования.
За образец тестирования мы взяли лексикографический перебор, т.к. метод перебора единственный дает абсолютно верный результат. Время работы такого алгоритма растет в соответствии (n-1)!, гдеn– число вершин графа.
Мы реализовали перебор написанный на Pascal.
Мы применяли полный перебор без повторений, таким образом мы можем работать с графами, в которых элементы c[i][j] иc[j][i] не равны.
В виду этих свойств является выгодным использовать более долгий, но наиболее точный алгоритм в качестве образца.
В качестве исследуемого метода мы взяли Жадный алгоритм. В данной работе мы задались целью изучить поведение жадного алгоритма, и соответствие результатов Жадного алгоритма с перебором.
Жадный алгоритм реализован на Pascal.
Для наибольшей наглядности и более комфортного тестирования мы создали графическую оболочку, в которой можно проследить результат работы сразу нескольких алгоритмов, а также время их выполнения.
3.2. Работа с приложением.
Запустить приложение (смотреть Help).
В Главном меню выбрать пункт: Опции ► Редактор.
В появившемся окне ввести матрицу стоимостей, в соответствии с указаниями в файле помощи (В основном окне: Помощь ► Помощь, либо нажать F1).
Для решения задачи нажать кнопку «Решить» (в окне редактирования матрици).
Поскольку наши алгоритмы выделены в отдельные DLLфайлы, что позволяем сторонним программистам писать свои алгоритмы не зависимо от языка программирования, то Вам достаточно отметить галочками в следующем окне те из них, которыми Вы хотите решить задачу. Затем нажать «Решить».
В последнем окне вы получите результат работы отмеченных в предыдущем окне алгоритмов.
Дополнительную информацию можно найти в файле помощи. Этим методом был протестирован Жадный алгоритм.
3.3. Жадный алгоритм.
В качестве начального пункта отправления мы выбрали город номер 1 и протестировали для таблиц разных размерностей.
Тестовая матрица 1: матрица 6 x 6
Вход:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
x |
13 |
7 |
5 |
2 |
9 |
|
2 |
8 |
x |
4 |
7 |
5 |
x |
|
3 |
8 |
4 |
x |
3 |
6 |
2 |
|
4 |
5 |
8 |
1 |
x |
0 |
1 |
|
5 |
x |
6 |
1 |
4 |
x |
9 |
|
6 |
10 |
0 |
8 |
3 |
7 |
x |
Выход:
|
Метод |
Путь |
Время выполненмя |
Длинна |
|
Перебор Pascal |
1→5→3→4→6→2→1 |
0 мс |
15 |
|
Жадный алг. |
1→5→3→6→2→4→1 |
0 мс |
17 |
Тестовая матрица 2: матрица 10 x 10
Вход:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
x |
12 |
14 |
10 |
2 |
5 |
7 |
8 |
2 |
13 |
|
2 |
8 |
x |
14 |
8 |
5 |
8 |
7 |
3 |
2 |
2 |
|
3 |
11 |
10 |
x |
1 |
2 |
20 |
15 |
7 |
0 |
19 |
|
4 |
2 |
6 |
1 |
x |
11 |
10 |
10 |
13 |
15 |
8 |
|
5 |
3 |
6 |
3 |
13 |
x |
8 |
5 |
9 |
9 |
9 |
|
6 |
1 |
6 |
21 |
2 |
9 |
x |
12 |
5 |
3 |
4 |
|
7 |
7 |
12 |
16 |
3 |
5 |
3 |
x |
11 |
16 |
20 |
|
8 |
9 |
2 |
0 |
14 |
7 |
4 |
18 |
x |
2 |
13 |
|
9 |
11 |
1 |
9 |
7 |
7 |
7 |
20 |
4 |
x |
17 |
|
10 |
12 |
3 |
11 |
1 |
9 |
8 |
3 |
5 |
14 |
x |
Выход:
|
Метод |
Путь |
Время выполненмя |
Длинна |
|
Перебор Pascal |
1→5→7→6→8→3→9→2→10→4→1 |
320мс |
21 |
|
Жадный алг. |
1→5→9→4→3→7→10→6→2→8→1 |
0 мс |
82 |