
- •Содержание:
- •1. Матрицы. Основные понятия и определения. Действия над матрицами
- •Действия над матрицами
- •1. Сложение матриц
- •2. Умножение матрицы на число
- •Общий множитель также можно выносить за скобку
- •3. Умножение матриц
- •1) Умножение матрицы-строки на матрицу-столбец
- •2) Умножение матриц
- •3) Умножение матрицы-столбца на матрицу-строку
- •4. Возведение в степень
- •5. Транспонирование матриц
- •2. Определители. Вычисление определителей
- •Свойства определителей
- •3. Обратная матрица. Ранг матрицы
- •Правило вычисления ранга матрицы
- •4. Система линейных алгебраических уравнений
- •4.1. Способы решения системы n линейных уравнений с n неизвестными. Матричный способ и метод Крамера
- •4.2. Способ решения системы m линейных уравнений с n неизвестными – метод Гаусса (метод последовательного исключения переменных)
- •Второй метод вычисления обратной матрицы.
- •Задачи для контрольных заданий
- •1. Задание по теме «Матрицы. Определители. Системы линейных алгебраических уравнений»
- •Литература Основная
- •Дополнительная
2. Определители. Вычисление определителей
Рассмотрим в общем виде систему двух линейных уравнений с двумя неизвестными
![]() (10)
(10)
Допустим,
что система имеет решение и пара
![]() составляет решение, так что оба уравнения
уже обратились в верные равенства. Решая
систему уравнений, получим решение вида
составляет решение, так что оба уравнения
уже обратились в верные равенства. Решая
систему уравнений, получим решение вида
![]() ,
,
![]() (11)
(11)
Если
![]() ,
то наши рассуждения не приводят ни к
какому результату, и поэтому будем
полагать что
,
то наши рассуждения не приводят ни к
какому результату, и поэтому будем
полагать что
![]() .
Для выражения
.
Для выражения
![]() существует специальное название
определитель
матрицы
существует специальное название
определитель
матрицы![]() и специальное обозначение:
и специальное обозначение:
![]() , (12)
, (12)
где
![]() .
.
Пример
2.1. Рассмотрим
A
=
![]() .
.
![]() .
.
Для определителей формулы (11) записываются в виде:
 ,
, (13)
(13)
Рассмотрим систему уравнений с тремя переменными и тремя неизвестными
 (14)
(14)
Запишем его в матричном виде:
 (15)
(15)
Решая данную систему уравнений и вводя обозначение:
 (16)
(16)
можно показать, что решение системы
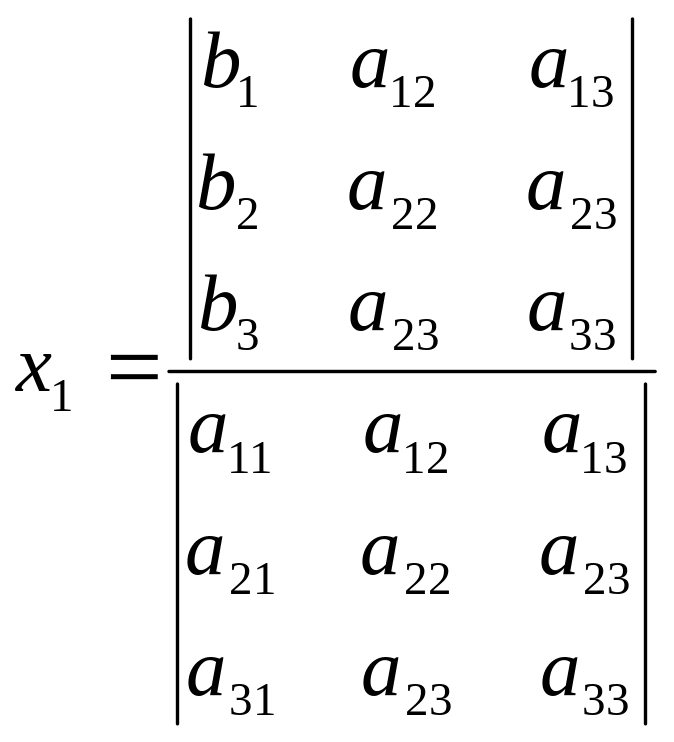 ,
, ,
,
Итак,
мы показали, что формулы для решения в
общем виде линейных систем уравнений
при
![]() и
и
![]() имеют сходную структуру и основную роль
в них играют определители второго
порядка
имеют сходную структуру и основную роль
в них играют определители второго
порядка
![]()
и третьего порядка
Оба эти выражения представляют собой алгебраические суммы произведений элементов матриц, причём эти произведения составляются по одному элементу из каждой строки и по одному из каждого столбца. Все такие произведения входят в состав определителя. Произведения снабжаются знаками плюс или минус по определённому правилу.
С каждой квадратной матрицей свяжем определенную численную характеристику, называемую определителем, соответствующим этой матрице.
Обозначение:
 .
.
Определение 2.1.
Определителем
матрицы
![]() первого
порядка,
называется сам элемент
первого
порядка,
называется сам элемент
![]() :
:
![]() .
.
Определение 2.2.
Определителем
матрицы
![]() второго
порядка,
называется число
второго
порядка,
называется число
![]() .
.
Определение 2.3.
Определителем матрицы третьего порядка, называется число
![]()
Последнее равенство вычисляется по правилу Саррюса (часто его называют правилом треугольника):

а (+) б (–)
Пример 2.2.
Вычислить
определитель
![]() .
.
Решение.
![]()
Определитель третьего порядка может быть преобразован следующим образом:
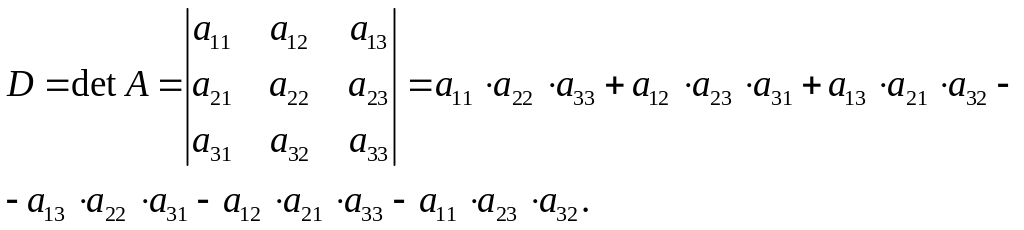
Пример 2.3.
Вычислить
определитель
 .
.
Решение.

Определение 2.4.
Определителем (детерминантом) n-го порядка называется число D, равное алгебраической сумме n! слагаемых, каждое из которых есть произведение n множителей aij, являющихся элементами ровно одной строки и ровно одного столбца. Обозначение:
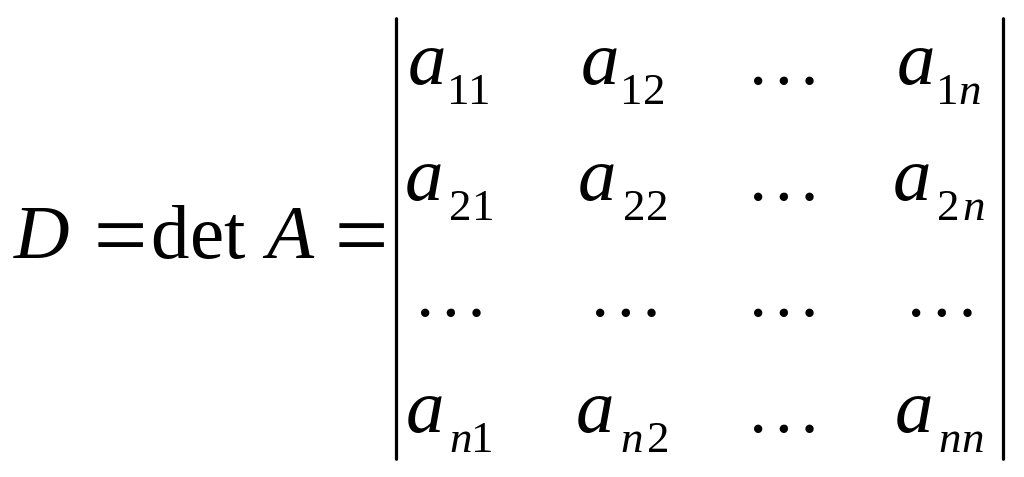 (17)
(17)
Определение 2.5.
Минором
элемента
![]() квадратной матрицы
-го
порядка называется определитель матрицы
(
квадратной матрицы
-го
порядка называется определитель матрицы
(![]() )-го
порядка, остающийся после вычеркивания
-й
строки и
-го
столбца данной матрицы
-го
порядка (то есть строки и столбца на
пересечении которых стоит элемент
)-го
порядка, остающийся после вычеркивания
-й
строки и
-го
столбца данной матрицы
-го
порядка (то есть строки и столбца на
пересечении которых стоит элемент
![]() ).
).
Обозначение:
![]() .
.
Пример
2.4. Вычислите
определитель

Решение.
 2ая
строка
+1ая,
умноженная на 2;
2ая
строка
+1ая,
умноженная на 2;
3я строка +1ая, умноженная на -3, 4ая строка +1я, умноженная на 1 =
= разложим
по элементам I-го
столбца:
разложим
по элементам I-го
столбца:

Определение 2.6.
Алгебраическим
дополнением
элемента
.
называется его минор, взятый со знаком
![]() ,
где
,
где
![]() – сумма номеров строки и столбца, на
пересечении которых расположен этот
элемент
– сумма номеров строки и столбца, на
пересечении которых расположен этот
элемент
![]() .
(18)
.
(18)
Пусть задана матрица A размером 4х4:
 ,тогда
,тогда 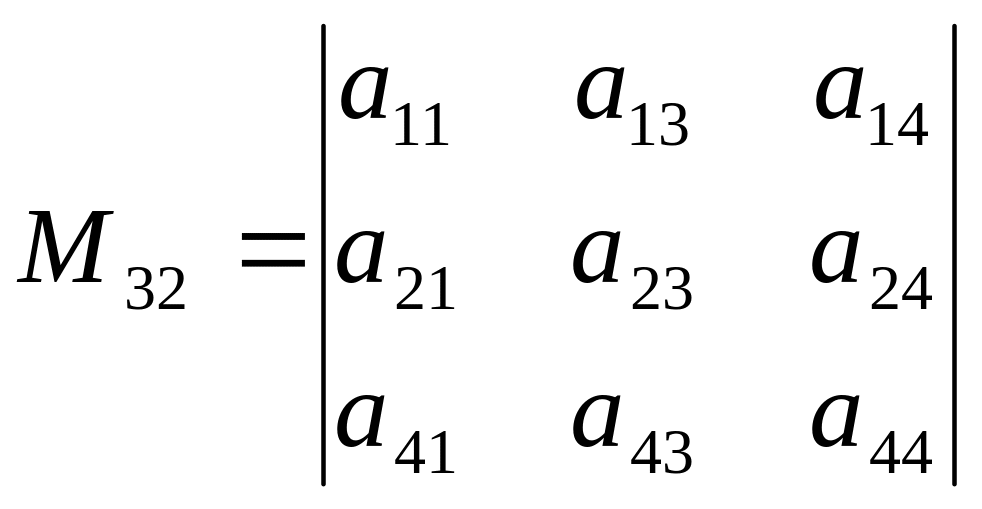 ,
,
![]() .
.
Заметим,
что ![]() ,
если
- четное число,
,
если
- четное число,
![]() ,
если
-
нечетное.
,
если
-
нечетное.
Теорема 2.1 (Лапласа).
Определитель матрицы -го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения
![]() .
(19)
.
(19)
– разложение по -й строке.
![]() (20)
(20)
(разложение по элементам i-ой строки; i=1..n);
![]() (21)
(21)
(разложение по элементам j-ого столбца; j=1..n);
