Вычет в бесконечно удалённой точке
– бесконечно
удалённая точка, если
в множестве
нет особых точек функции
.
Введём замену переменных:
.
Тогда, если
,
то
,
следовательно, для любой функции
нужно исследовать не
,
а
.
Функцию
можно разложить в ряд:
.
Тогда возможны следующие варианты:
Устранимая особая точка:
,
если
.Полюс порядка k:
или
.Существенно особая точка:
бесконечно много.
Вычет в бесконечно удалённой точке:
.
Если функция имеет лишь конечное количество особых точек, то сумма всех её вычетов во всех особых точках, включая равна 0.
Т.к. n – конечно, то
для
будет
.
При этом
сходится для
.
Следовательно,
(т.к.
).
Преобразование Лапласа
Пусть
определена на
,
кусочно непрерывна,
и
и
.
Тогда
,
где
.
Функция
называется оригиналом,
– изображением.
Найдём производную оригинала:
.
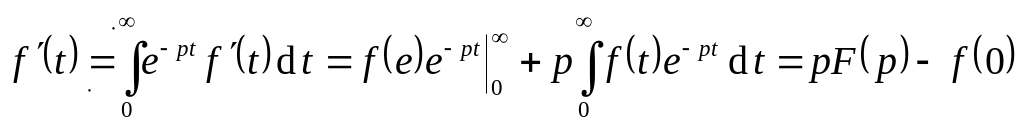Свойства изображения:
– аналитическая функция в
.
Если
,
то в D
равномерно сходится, т.к.
(при
)
.
Пусть есть замкнутый контур .
Тогда
,
т.к.
– аналитическая функция.
Обращение
.
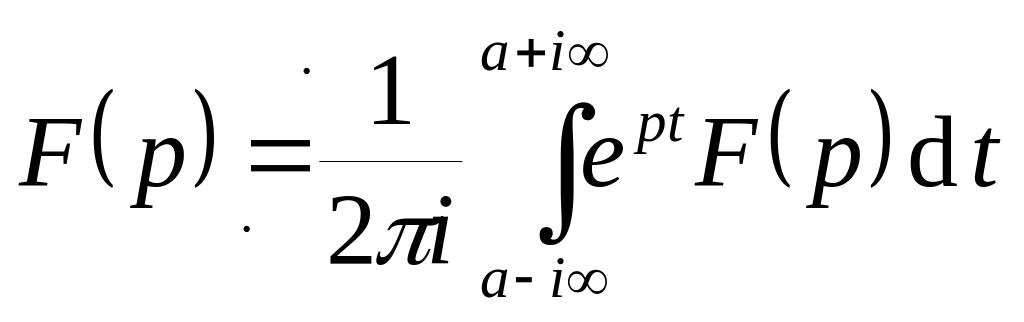Свойства преобразования Лапласа:
Линейность:
.
.
.
,
если
непрерывна.
.
,
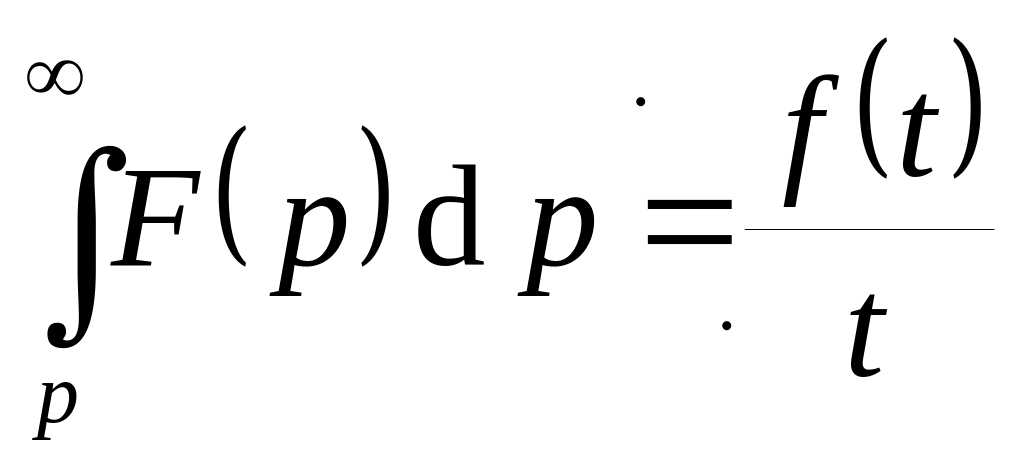если он существует.
Изображения некоторых функций:
Функция Хевисайда:
.
.
.
.(«интегральный синус»):
.
Теорема смещения:
.
Теорема умножения: Если
,
то
– «свёртка».
.
.
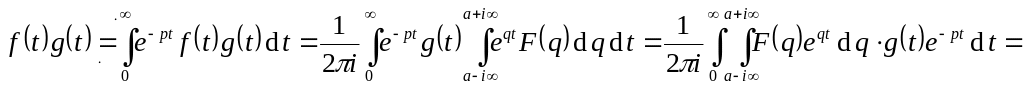
Рассмотрим задачу Коши:
.
Будем рассматривать более простой
случай:
.
(Если условия такие:
,
то можно сделать замену переменных,
удовлетворяющую системе:
).
Сначала решим такое уравнение:
.
Это обычное линейное дифференциальное
уравнение второго порядка с частным
решением
.
В результате получается функция
– решение этого уравнения. Тогда
(т.к.
)
.
При этом
.
Принцип максимума модуля
Пусть
аналитична в области G
и интегрируема вдоль L
– границы G.
Тогда
.
Тогда
,
причём
.
Предположим, что
и
.
Тогда
(здесь R: область
)
и
.
Утверждение:
для
.
Предположим, что
.
Тогда для
для
будет
.
Тогда
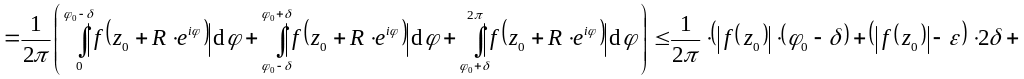
– противоречие. Следовательно,
.
Тогда
для
.
Пусть
.
Условия Коши-Римана:
.
При этом
.
Аналогично и
и
.
.
Таким образом,
.
Аналогично
.
Отсюда следует, что
и
,
т.е.
.