Теория функций комплексных переменных.
Число
называют мнимой единицей. Любое
комплексное число представляется в
виде
.
При этом
– вещественная часть,
– мнимая часть.
Число
называется комплексно сопряжённым
числу
.
Правила действий с комплексными числами:
Сложение/вычитание:
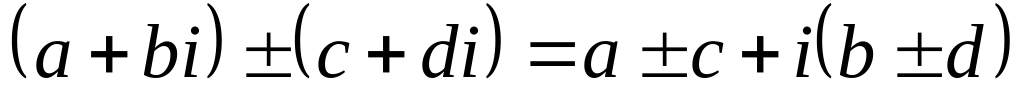.Умножение:
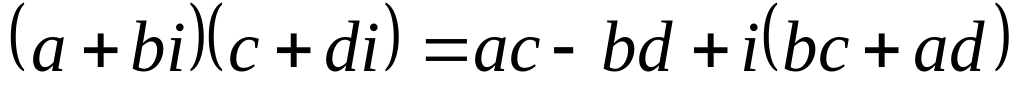.Деление:
.
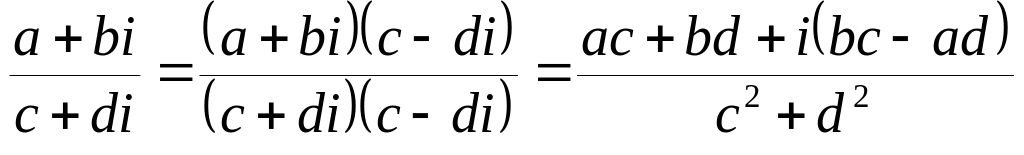Основная теорема высшей алгебры: какое бы ни было уравнение с биномиальными членами, у него есть хотя бы одно решение.
Если
– корень уравнения
,
то, поделив многочлен слева на
,
получим:
,
где
– в общем случае многочлен степени
меньшей, чем
(здесь – число). При этом
.
Получим уравнение:
.
У него также есть корень. Следовательно,
у уравнения n-й степени
есть n корней:
.
П
усть
есть два комплексных числа
и
.
Им можно сопоставить два вектора:
и
.
Перейдя в полярные координаты, получим:
– модуль комплексного числа,
(аргумент z). Если
имеется в виду неоднозначное определение
,
то arg пишется с большой
буквы:
.
Произведение комплексных чисел в
тригонометрической форме:
Отсюда можно получить формулы для
тригонометрических функций:
.
Извлечение корня: Пусть
.
Тогда, если
,
то
,
а
.
Последовательность
комплексных чисел
имеет предел при
,
равный u
,
если
(вещественный).
Критерий сходимости Коши:
сходится тогда и только тогда, когда
она фундаментальна, т.е. для
для
будет
.
Ряд
сходится тогда и только тогда, когда
для
:
для
и
будет
.
– дзета-функция Римана
.
Уравнение
имеет, по предположению Римана, решение
только при
для
– не доказано.
для
для
будет
.
для
будет
.
.
непрерывна в точке
,
если
.
Теорема Абеля: Рассмотрим
.
Пусть в точке
ряд сходится. Тогда он сходится для
.
Если же ряд расходится в точке
,
то он будет расходиться для
.
Пусть
сходится. Возьмём
.
Тогда
,
следовательно, для
для
будет
.
Рассмотрим
,
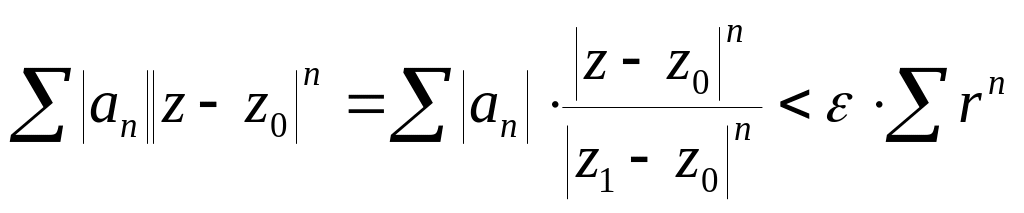где
.
При этом, если
,
то
сходится (по критерию Коши:
),
следовательно, сходится и исходный ряд.
Обобщённый признак Коши: Рассмотрим
.
Пусть
.
Если
,
то ряд сходится, если
,
то он расходится.
Обобщённый признак Даламбера: Если
,
то ряд сходится, а если
,
то ряд расходится.
Функцию комплексных переменных можно
представить так:
,
где u и v
– вещественные функции. Таким образом,
функция f переводит
точки
в точки
,
то есть фактически это не функция, а
отображение.
Пусть
,
a – вещественное,
.
Тогда
Пусть
.
Если
,
то
(бесконечно удалённая точка).
Варианты геометрии Лобачёвского
Плоскостью служит верхняя полуплоскость
вида
.
Геометрическое место точек
– абсолют. В качестве прямых служат
полуокружности с центром, началом и
концом на абсолюте, а также лучи,
перпендикулярные абсолюту.
К
ак
найти расстояние между
и
?
Рассмотрим
– ангармоническое соотношение 4-х точек.
в качестве расстояния можно взять
.
Рассмотрим уравнение:
.
Пусть
.
Таким образом,
.
Другое уравнение:
,
т.е.
.
Дифференциальное исчисление
.
Тогда
.
Пусть
и
.
Тогда:
;
;
.
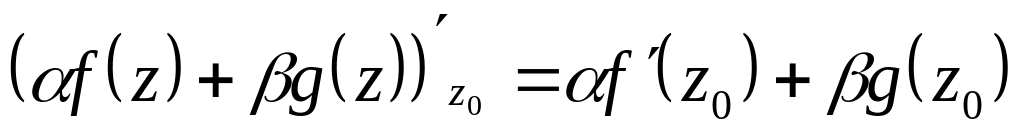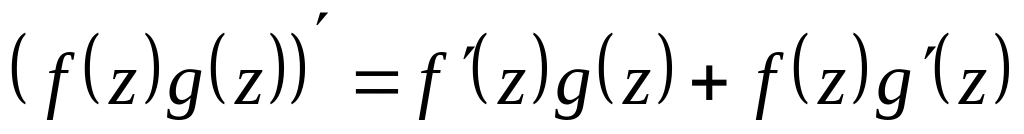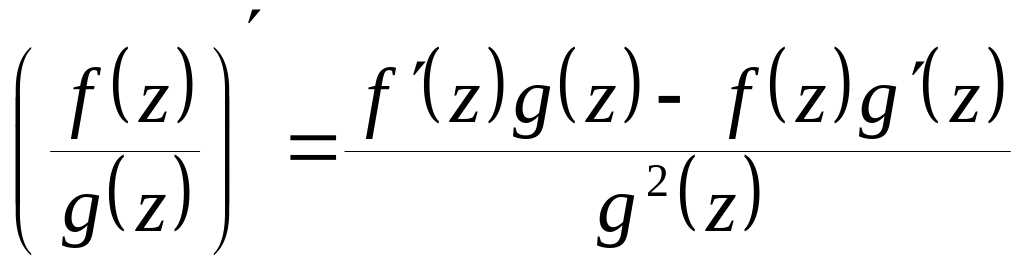Пусть есть
,
и
.
Рассмотрим
.Т.к.
и
,
то
.
Производная обратной функции: пусть
есть
и
.
Если
переводит точки из области z
в область W, то обратная
функция – из области W
в область z. При этом
обратная функция существует только в
том случае, когда точке из области z
отвечает одна и только одна точка в
области W.
.
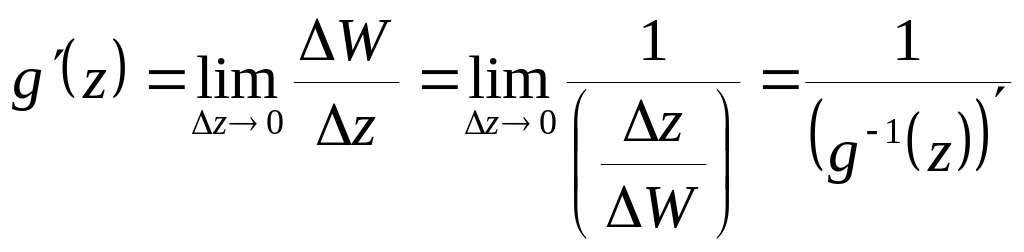Пусть дана функция
.
Проверим, будет ли
оставаться тем же при стремлении
к 0 по разным направлениям (например,
параллельном сначала оси x,
а потом – оси y):
;
.
Таким образом, это равенство выполняется
при
– условия Коши-Римана.
Пусть
и
дифференцируемые функции двух переменных
в окрестности точки
и пусть выполняются условия Коши-Римана.
Тогда
.
Т.к.
и
непрерывны в точке
,
то
и
.
Из условий Коши-Римана следует, что
.
Тогда
.
Все формулы дифференцирования сохраняются.
Геометрический смысл производной
П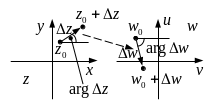
усть
задано отображение
.
Тогда
,
где
– бесконечно малая. Таким образом,
модуль производной – коэффициент
локального растяжения в окрестности
точки
.
.
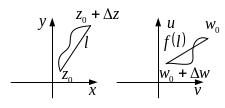стремится
к углу наклона касательной к кривой
.
стремится к углу наклона касательной
к кривой l.
П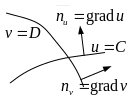
усть
.
Рассмотрим линии
,
.
Утверждение: они ортогональны.
(из условий Коши-Римана)
.
Интегральное исчисление
Пусть задана спрямляемая линия l.
Разобьём её точками
.
Тогда комплексный криволинейный интеграл
,
где
,
если этот предел существует.
Рассмотрим его:
.
Таким образом,
,
если u и v
кусочно непрерывны и ограничены на
спрямляемой линии l.
Существует, если u и v кусочно непрерывны и ограничены на спрямляемой линии l.
Зависит от направления.
Линейность: если есть и , интегрируемые вдоль l, то для
и b
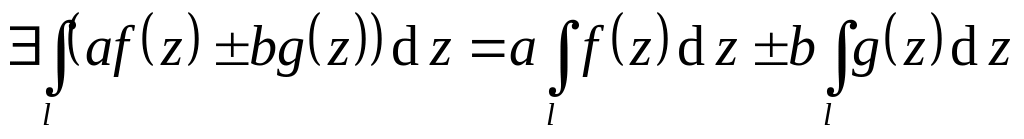.Аддитивность: если
и
,
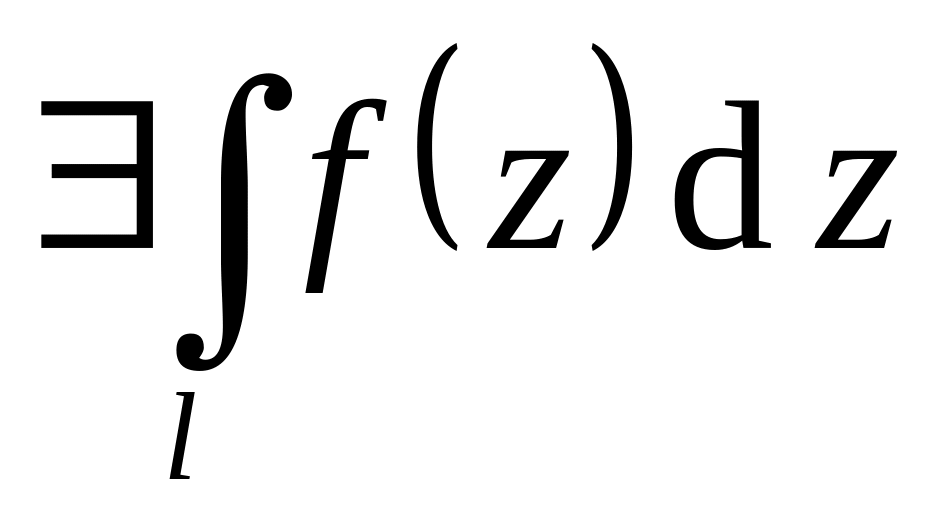то
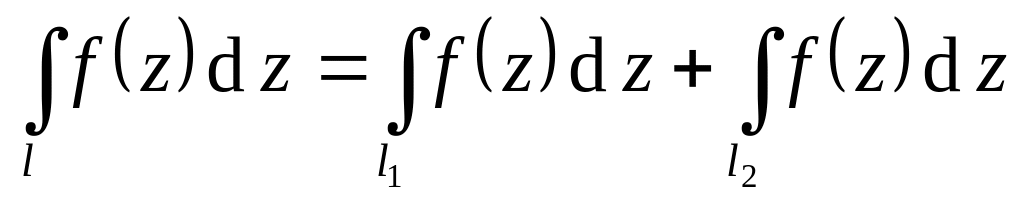.Оценка: если
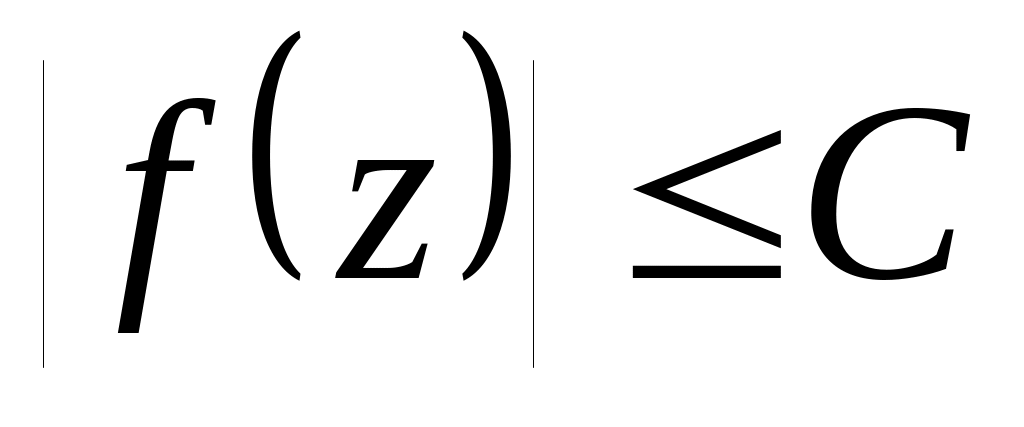при
,
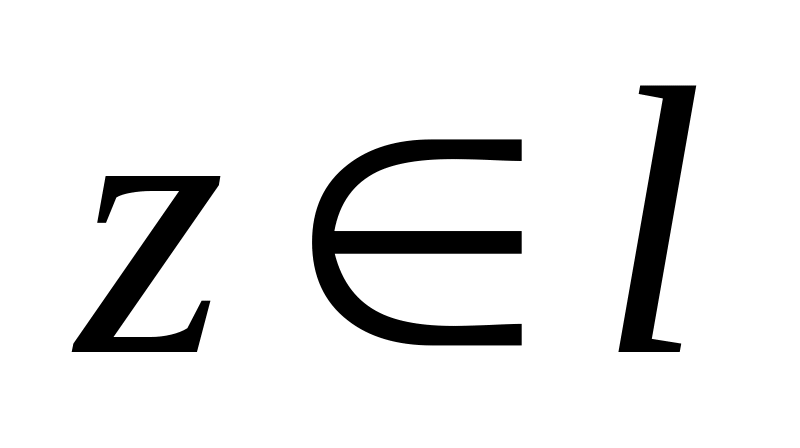то
.
.
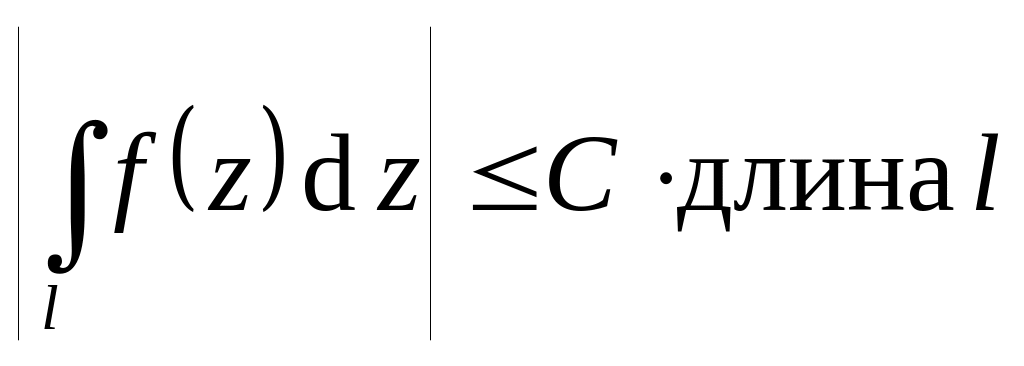Если выполняются условия Коши-Римана
и известна функция
,
то можно найти
.
Если L
– замкнутый контур, ограничивающий
односвязную область
и
существует при
,
то
.
Пусть
.
Тогда
(по формуле Грина)
(из условий Коши-Римана)
.
Интегральная теорема Коши: Пусть
задана многосвязная область D,
– её граница,
– границы внутренних областей, функция
непрерывна на всех границах и имеет
непрерывную производную в области D.
Тогда
.
С
оединим
произвольным образом все
с . В результате
получим одну границу, охватывающую как
область D, так и
внутренние области. Направление обхода
вдоль этой границе по внутренним областям
будет отрицательно, т.к. точки внутренней
области при этом будут лежать справа.
Следовательно,
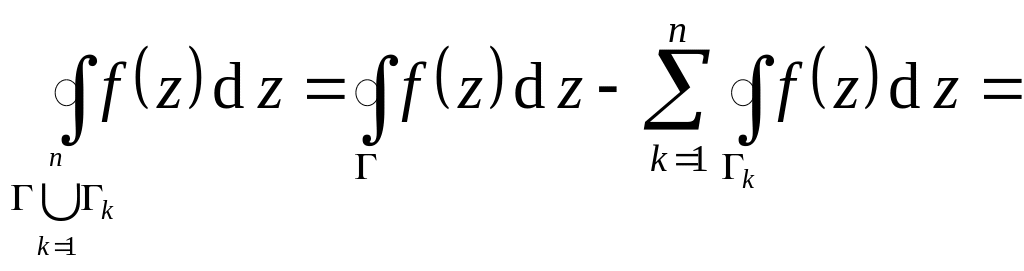(по теореме)
.
Интегральная формула Коши: Если
точка
принадлежит области D,
то
,
где
– граница области D.
Возьмём окружность радиуса R
с центром в точке
так, чтобы все её точки принадлежали D.
Тогда
.
Уравнение окружности:
,
где
,
следовательно,
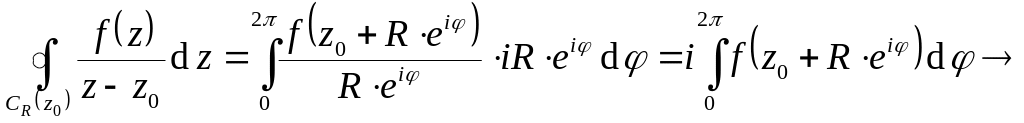(при
)
.
Интегральная формула Коши для
производных аналитических функций:
,
где L
– контур, охватывающий
.
Рассмотрим сначала
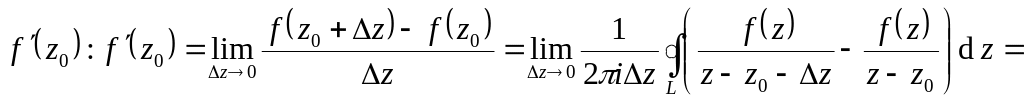
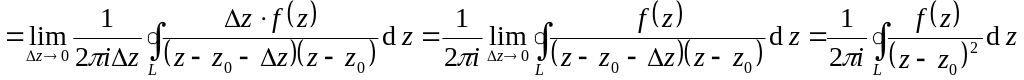.Предположим теперь, что формула выполняется для
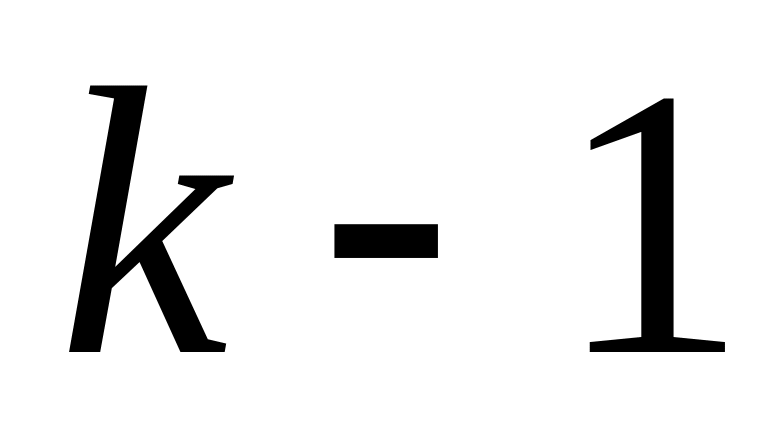-й
производной и рассмотрим
.
.
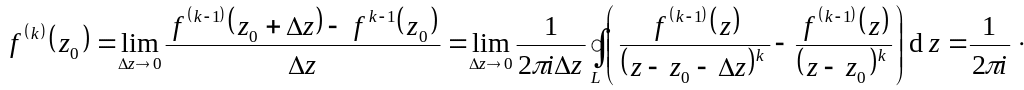
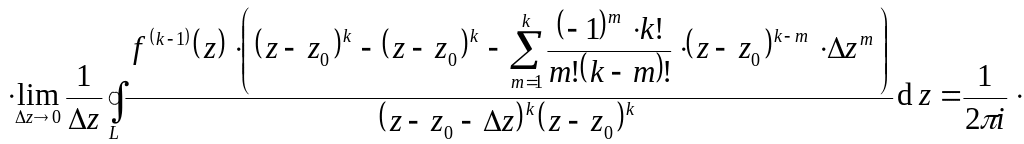
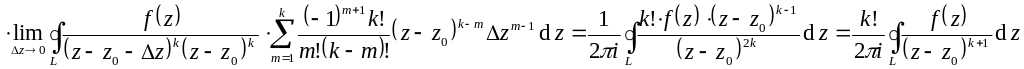Теорема Лиувилля: Если
– аналитическая функция на всей плоскости
комплексных переменных и
,
то она неограниченна.
.
Тогда
.
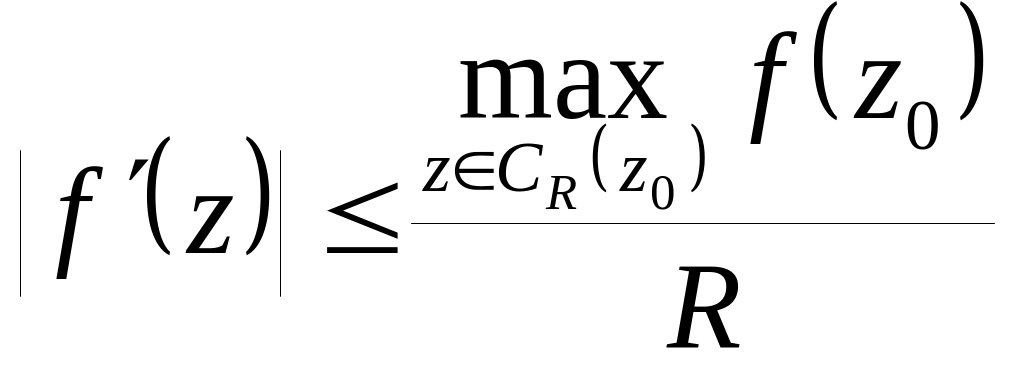Предположим, что
ограничена, т.е.
для
будет
.
Тогда
,
т.к. R – произвольно,
а A – ограниченно,
следовательно,
.
Таким образом, если
,
то
неограниченна.
Основная теорема высшей алгебры:
Для многочлена
,
где
– комплексные числа,
.
Пусть
для
и пусть
.
Тогда, т.к.
,
то
аналитична везде. Возьмём
.
Тогда
(т.к.
)
.
При достаточно больших R
будет
.
Тогда
,
т.е.
для
будет
.
Область
– ограниченная,
непрерывна везде, следовательно,
ограничена в области
(по теореме Вейерштрасса), т.е.
при
.
Таким образом, для
– ограниченна везде и, т.к. она аналитична
везде, то по теореме Лиувилля
,
что противоречит условию.
,
причём возможно, что
и при
:
.
По основной теореме
.
Тогда
,
где R – остаток, степень
R меньше степени
,
т.е.
.
Аналогично,
и т.д.
Теорема Морера: Если непрерывна в односвязной области D и , где L – контур, лежащий в этой области, то аналитична в этой области.
В
ведём
функцию
,
где
– произвольный контур от точки z
до точки
,
целиком лежащий в D.
Рассмотрим
,
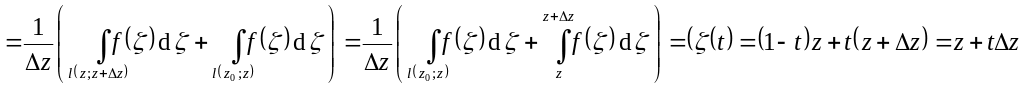
т.е.
непрерывна. Таким образом,
.
Тогда
.