
- •Глава 0. Основные понятия теории дифференциальных уравнений
- •Глава 1. Уравнения первого порядка.
- •§ 1.1 Уравнения, разрешённые относительно производных; их геометрическая интерпретация.
- •§ 1.2 Уравнение с разделяющимися переменными.
- •§1.3 Уравнения в полных дифференциалах. Интегрирующий множитель.
- •§ 1.4 Линейные уравнения
- •§ 1.5 Теорема о существовании и единственности решения задачи Коши для уравнения, разрешённого относительно производной
- •§ 1.6 Уравнения, не разрешённые относительно производных.
- •Глава 2. Уравнения порядка выше первого.
- •§ 2.1 Теорема о существовании и единственности решения задачи Коши.
- •§ 2.2 Линейные уравнения. Общие свойства линейных уравнений.
- •§ 2.3 Решение однородных линейных уравнений
- •§ 2.4 Решение однородных линейных уравнений с постоянными коэффициентами
- •§2.5 Формула Остроградского-Лиувилля
- •§2.6 Решения неоднородных линейных уравнений. Метод вариации произвольных переменных. Функция Коши.
- •Глава 3. Краевые задачи для линейного уравнения второго порядка
- •§ 3.2 Решение неоднородных краевых задач. Функция Грина.
- •§3.3 Однородные краевые задачи. Собственные значения и собственные функции.
- •Глава 0. Основные понятия теории дифференциальных уравнений
- •Глава 1. Уравнения первого порядка.
- •§ 1.1 Уравнения, разрешённые относительно производных; их геометрическая интерпретация.
- •§ 1.2 Уравнение с разделяющимися переменными.
- •§1.3 Уравнения в полных дифференциалах. Интегрирующий множитель.
- •§ 1.4 Линейные уравнения
- •§ 1.5 Теорема о существовании и единственности решения задачи Коши для уравнения, разрешённого относительно производной
- •§ 1.6 Уравнения, не разрешённые относительно производных.
- •Глава 2. Уравнения порядка выше первого.
- •§ 2.1 Теорема о существовании и единственности решения задачи Коши.
- •§ 2.2 Линейные уравнения. Общие свойства линейных уравнений.
- •§ 2.3 Решение однородных линейных уравнений
- •§ 2.4 Решение однородных линейных уравнений с постоянными коэффициентами
- •§2.5 Формула Остроградского-Лиувилля
- •§2.6 Решения неоднородных линейных уравнений. Метод вариации произвольных переменных. Функция Коши.
- •Глава 3. Краевые задачи для линейного уравнения второго порядка
- •§ 3.2 Решение неоднородных краевых задач. Функция Грина.
- •§3.3 Однородные краевые задачи. Собственные значения и собственные функции.
- •Глава 4. Системы дифференциальных уравнений.
- •§4.1 Нормальные системы.
- •§1.2 Линейные системы. Общие свойства линейных систем.
- •§4.3 Решение однородных линейных систем
- •§4.1. Решение однородных линейных систем с постоянными коэффициентами
- •Глава 5. Устойчивость решений дифференциальных уравнений
- •§5.1 Понятие устойчивости по Ляпунову. Асимптотическая устойчивость. Точки покоя.
- •§5.2 Простейшие типы точек покоя на плоскости
- •§5.3 Исследование на устойчивость по первому приближению
- •§5.4 Прямой (второй) метод Ляпунова
- •Глава 6. Уравнения с частными производными первого порядка.
- •§6.2. Решение однородных линейных уравнений
- •§6.3. Решение квазилинейных уравнений
- •§6.4. Решение задачи Коши для квазилинейных уравнений
- •Глава 4. Системы дифференциальных уравнений.
- •§4.1 Нормальные системы.
- •§1.2 Линейные системы. Общие свойства линейных систем.
- •§4.3 Решение однородных линейных систем
- •§4.1. Решение однородных линейных систем с постоянными коэффициентами
- •Глава 5. Устойчивость решений дифференциальных уравнений
- •§5.1 Понятие устойчивости по Ляпунову. Асимптотическая устойчивость. Точки покоя.
- •§5.2 Простейшие типы точек покоя на плоскости
- •§5.3 Исследование на устойчивость по первому приближению
- •§5.4 Прямой (второй) метод Ляпунова
- •Глава 6. Уравнения с частными производными первого порядка.
- •§6.2. Решение однородных линейных уравнений
- •§6.3. Решение квазилинейных уравнений
- •§6.4. Решение задачи Коши для квазилинейных уравнений
§ 1.4 Линейные уравнения
Линейными уравнениями I-го
порядка будем называть уравнения вида
EMBED Equation.3
![]() .
Здесь EMBED Equation.3
– коэффициент линейного уравнения,
EMBED Equation.3
.
Здесь EMBED Equation.3
– коэффициент линейного уравнения,
EMBED Equation.3
![]() – неоднородность линейного уравнения.
– неоднородность линейного уравнения.
Если EMBED Equation.3
![]() ,
то уравнение называется неоднородным,
иначе – однородным. Если в уравнении
формально отбросить EMBED Equation.3
,
то получится соответствующее однородное
уравнение.
,
то уравнение называется неоднородным,
иначе – однородным. Если в уравнении
формально отбросить EMBED Equation.3
,
то получится соответствующее однородное
уравнение.
Будем полагать, что функции EMBED Equation.3
и EMBED Equation.3
определены на EMBED Equation.3
![]() .
Зафиксируем точку EMBED Equation.3
.
Зафиксируем точку EMBED Equation.3
![]() .
Дополним линейное уравнение начальным
условием EMBED Equation.3
.
В результате мы получили задачу Коши.
.
Дополним линейное уравнение начальным
условием EMBED Equation.3
.
В результате мы получили задачу Коши.
Пусть EMBED Equation.3 и EMBED Equation.3 непрерывны на EMBED Equation.3 . Тогда задача Коши имеет единственное решение, определённое на EMBED Equation.3 .
Единственность: Пусть задача Коши имеет два различных решения EMBED Equation.3
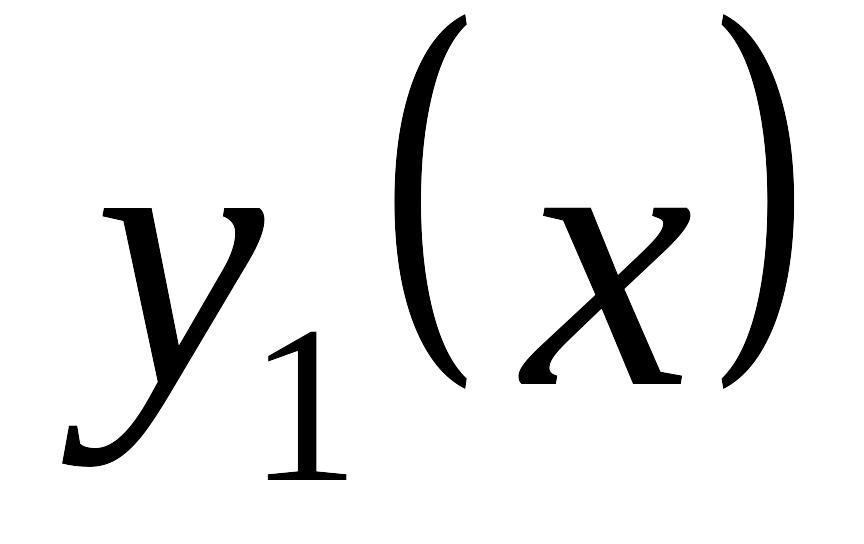 и EMBED Equation.3
и EMBED Equation.3
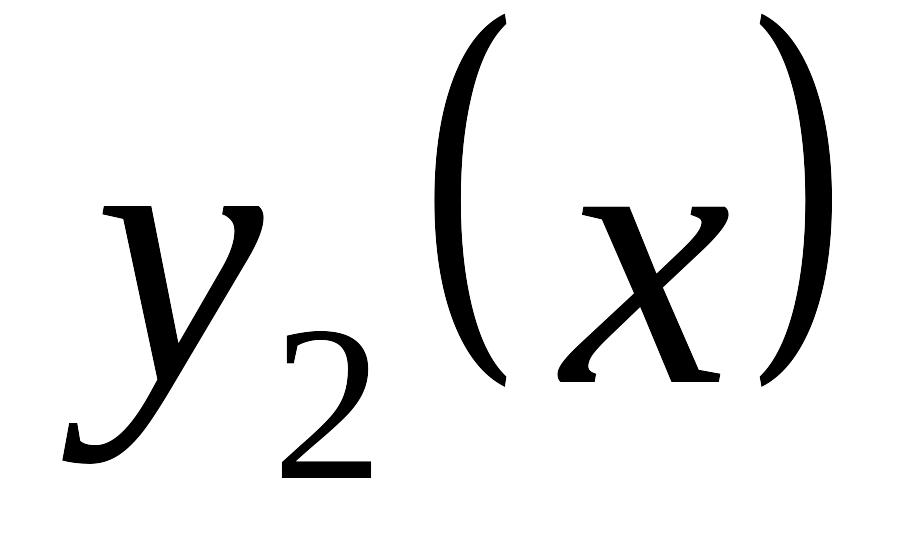 .
Тогда EMBED Equation.3
.
Тогда EMBED Equation.3
 удовлетворяет уравнению EMBED Equation.3
удовлетворяет уравнению EMBED Equation.3
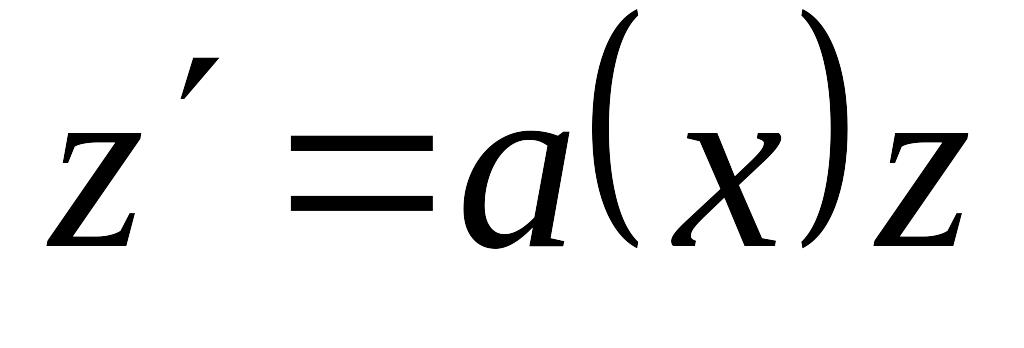 и начальному условию EMBED Equation.3
и начальному условию EMBED Equation.3
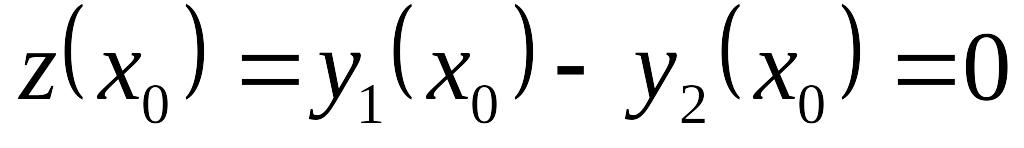 .
Имеем уравнение с разделяющимися
переменными, EMBED Equation.3
.
Имеем уравнение с разделяющимися
переменными, EMBED Equation.3
 расходится, следовательно задача Коши
имеет единственное решение EMBED Equation.3
расходится, следовательно задача Коши
имеет единственное решение EMBED Equation.3
 (см. второе замечание § 1.2), что противоречит
условию.
(см. второе замечание § 1.2), что противоречит
условию.Существование: Пусть существует функция EMBED Equation.3
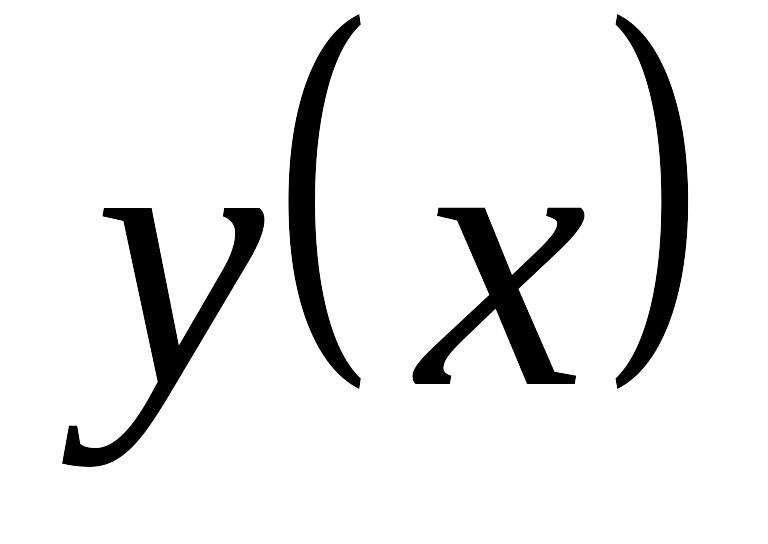 ,
являющаяся решением задачи Коши. Получим
представление для неё: EMBED Equation.3
,
являющаяся решением задачи Коши. Получим
представление для неё: EMBED Equation.3
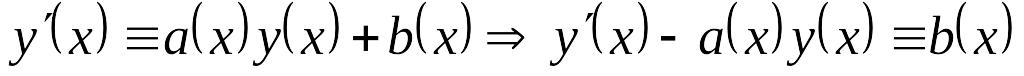 .
Умножим обе части тождества на EMBED
Equation.3
.
Умножим обе части тождества на EMBED
Equation.3
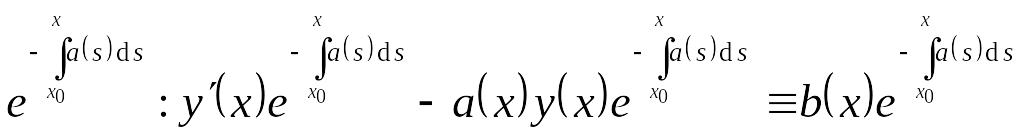 .
Преобразуем получившееся выражение:
EMBED Equation.3
.
Преобразуем получившееся выражение:
EMBED Equation.3
 .
Таким образом, решение задачи Коши,
если оно существует, представляется в
виде этого тождества. Рассмотрим его.
В правой части имеем непрерывно
дифференцируемую функцию, определённую
при EMBED Equation.3
.
Таким образом, решение задачи Коши,
если оно существует, представляется в
виде этого тождества. Рассмотрим его.
В правой части имеем непрерывно
дифференцируемую функцию, определённую
при EMBED Equation.3
 .
Подставив её в уравнение, проведя
преобразования в обратном порядке,
убедимся, что она – решение этого
уравнения. Таким образом, решения задачи
Коши существуют.
.
Подставив её в уравнение, проведя
преобразования в обратном порядке,
убедимся, что она – решение этого
уравнения. Таким образом, решения задачи
Коши существуют.
Линейное уравнение всегда
имеет интегрирующий множитель EMBED
Equation.3
![]() .
.
Способы решения линейных уравнений:
Метод интегрирующего множителя.
Метод вариации произвольной постоянной (метод Лагранжа) – это метод решения неоднородных уравнений. В нём можно выделить два этапа:
Решаем соответствующее однородное уравнение EMBED Equation.3
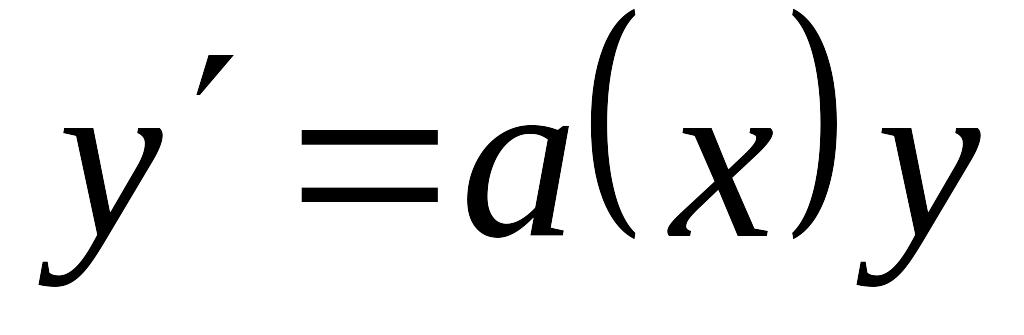 .
Общее решение – EMBED Equation.3
.
Общее решение – EMBED Equation.3
 (C – любое число).
(C – любое число).Полагаем EMBED Equation.3
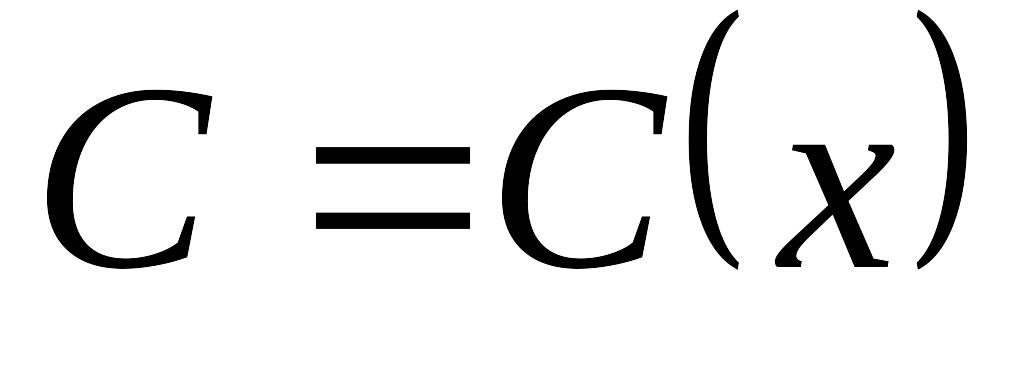 и ищем решение линейного уравнения в
виде EMBED Equation.3
и ищем решение линейного уравнения в
виде EMBED Equation.3
 .
Подставляем EMBED Equation.3
в уравнение: EMBED Equation.3
.
Подставляем EMBED Equation.3
в уравнение: EMBED Equation.3
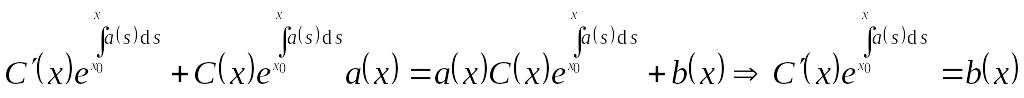 и EMBED Equation.3
и EMBED Equation.3
 .
Отсюда EMBED Equation.3
.
Отсюда EMBED Equation.3
 .
Подставим EMBED Equation.3
.
Подставим EMBED Equation.3
 в EMBED Equation.3
в EMBED Equation.3
 .
Здесь EMBED Equation.3
.
Здесь EMBED Equation.3
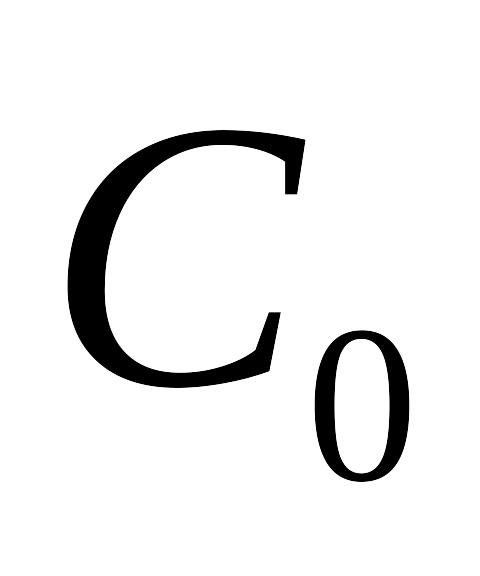 – любое число. Эта формула даёт общее
решение линейного уравнения.
– любое число. Эта формула даёт общее
решение линейного уравнения.
Следовательно, решение задачи Коши легко получить соответствующим EMBED Equation.3 . Общее решение неоднородного линейного уравнения, представляющееся суммой общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного линейного уравнения, можно получить, решив соответствующее однородное уравнение и подобрав каким-либо образом частное решение неоднородного уравнения.
Общие свойства линейных уравнений:
Пусть EMBED Equation.3 – решение уравнения EMBED Equation.3 . Тогда EMBED Equation.3
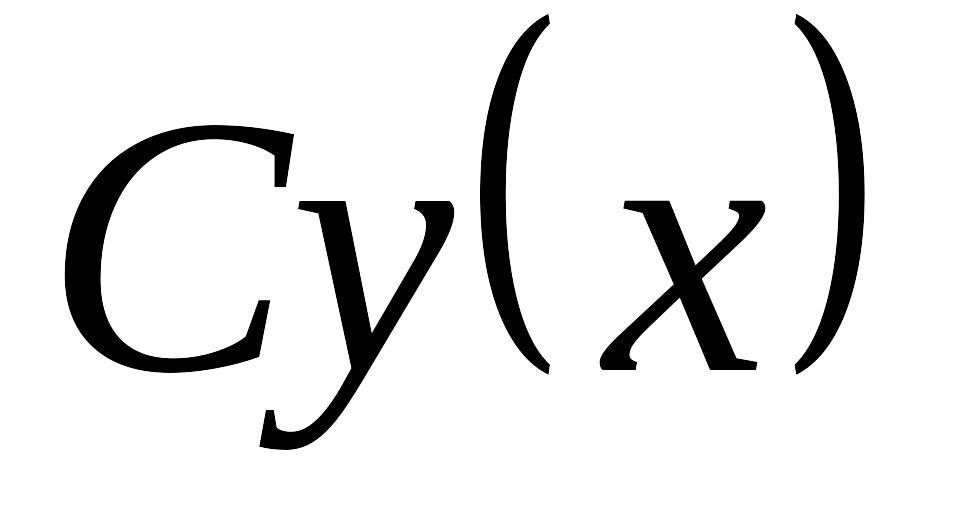 – тоже решение этого же уравнения.
– тоже решение этого же уравнения.Пусть EMBED Equation.3 и EMBED Equation.3 – решения уравнения EMBED Equation.3 . Тогда EMBED Equation.3
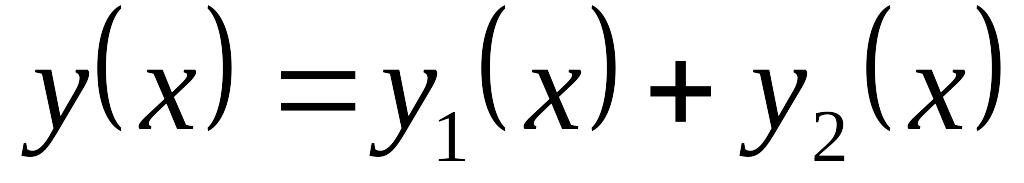 – тоже решения этого же уравнения.
– тоже решения этого же уравнения.Принцип суперпозиции: пусть в неоднородном уравнении EMBED Equation.3
 и EMBED Equation.3
и EMBED Equation.3
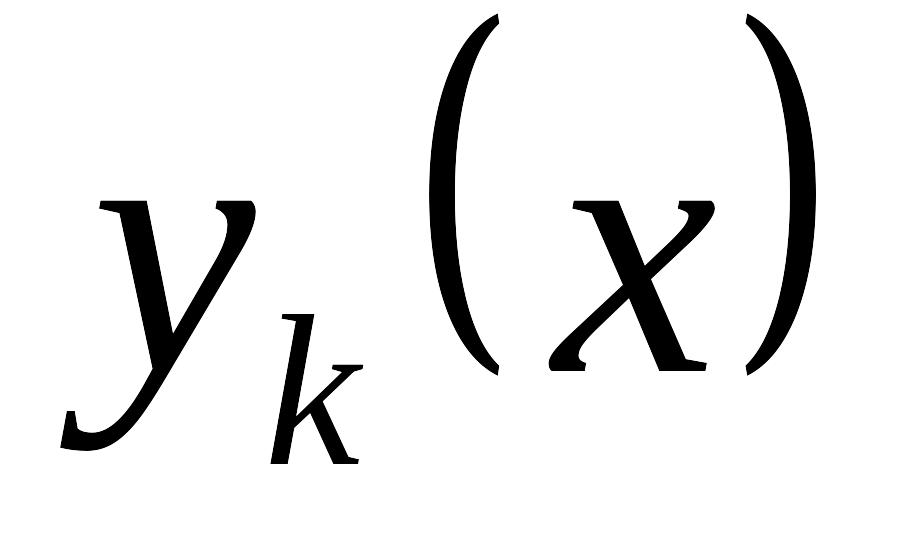 – решение уравнения EMBED Equation.3
– решение уравнения EMBED Equation.3
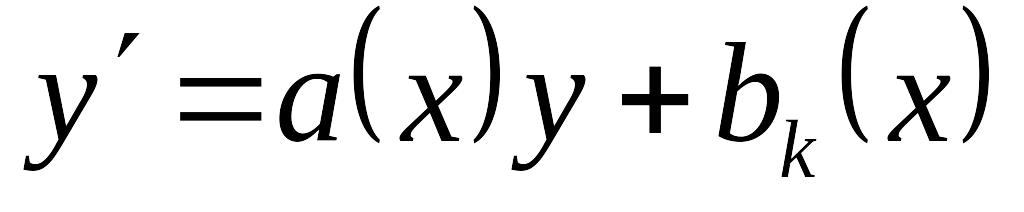 .
Тогда EMBED Equation.3
.
Тогда EMBED Equation.3
 – решение уравнения EMBED Equation.3
.
– решение уравнения EMBED Equation.3
.
