
- •Глава 0. Основные понятия теории дифференциальных уравнений
- •Глава 1. Уравнения первого порядка.
- •§ 1.1 Уравнения, разрешённые относительно производных; их геометрическая интерпретация.
- •§ 1.2 Уравнение с разделяющимися переменными.
- •§1.3 Уравнения в полных дифференциалах. Интегрирующий множитель.
- •§ 1.4 Линейные уравнения
- •§ 1.5 Теорема о существовании и единственности решения задачи Коши для уравнения, разрешённого относительно производной
- •§ 1.6 Уравнения, не разрешённые относительно производных.
- •Глава 2. Уравнения порядка выше первого.
- •§ 2.1 Теорема о существовании и единственности решения задачи Коши.
- •§ 2.2 Линейные уравнения. Общие свойства линейных уравнений.
- •§ 2.3 Решение однородных линейных уравнений
- •§ 2.4 Решение однородных линейных уравнений с постоянными коэффициентами
- •§2.5 Формула Остроградского-Лиувилля
- •§2.6 Решения неоднородных линейных уравнений. Метод вариации произвольных переменных. Функция Коши.
- •Глава 3. Краевые задачи для линейного уравнения второго порядка
- •§ 3.2 Решение неоднородных краевых задач. Функция Грина.
- •§3.3 Однородные краевые задачи. Собственные значения и собственные функции.
- •Глава 0. Основные понятия теории дифференциальных уравнений
- •Глава 1. Уравнения первого порядка.
- •§ 1.1 Уравнения, разрешённые относительно производных; их геометрическая интерпретация.
- •§ 1.2 Уравнение с разделяющимися переменными.
- •§1.3 Уравнения в полных дифференциалах. Интегрирующий множитель.
- •§ 1.4 Линейные уравнения
- •§ 1.5 Теорема о существовании и единственности решения задачи Коши для уравнения, разрешённого относительно производной
- •§ 1.6 Уравнения, не разрешённые относительно производных.
- •Глава 2. Уравнения порядка выше первого.
- •§ 2.1 Теорема о существовании и единственности решения задачи Коши.
- •§ 2.2 Линейные уравнения. Общие свойства линейных уравнений.
- •§ 2.3 Решение однородных линейных уравнений
- •§ 2.4 Решение однородных линейных уравнений с постоянными коэффициентами
- •§2.5 Формула Остроградского-Лиувилля
- •§2.6 Решения неоднородных линейных уравнений. Метод вариации произвольных переменных. Функция Коши.
- •Глава 3. Краевые задачи для линейного уравнения второго порядка
- •§ 3.2 Решение неоднородных краевых задач. Функция Грина.
- •§3.3 Однородные краевые задачи. Собственные значения и собственные функции.
- •Глава 4. Системы дифференциальных уравнений.
- •§4.1 Нормальные системы.
- •§1.2 Линейные системы. Общие свойства линейных систем.
- •§4.3 Решение однородных линейных систем
- •§4.1. Решение однородных линейных систем с постоянными коэффициентами
- •Глава 5. Устойчивость решений дифференциальных уравнений
- •§5.1 Понятие устойчивости по Ляпунову. Асимптотическая устойчивость. Точки покоя.
- •§5.2 Простейшие типы точек покоя на плоскости
- •§5.3 Исследование на устойчивость по первому приближению
- •§5.4 Прямой (второй) метод Ляпунова
- •Глава 6. Уравнения с частными производными первого порядка.
- •§6.2. Решение однородных линейных уравнений
- •§6.3. Решение квазилинейных уравнений
- •§6.4. Решение задачи Коши для квазилинейных уравнений
- •Глава 4. Системы дифференциальных уравнений.
- •§4.1 Нормальные системы.
- •§1.2 Линейные системы. Общие свойства линейных систем.
- •§4.3 Решение однородных линейных систем
- •§4.1. Решение однородных линейных систем с постоянными коэффициентами
- •Глава 5. Устойчивость решений дифференциальных уравнений
- •§5.1 Понятие устойчивости по Ляпунову. Асимптотическая устойчивость. Точки покоя.
- •§5.2 Простейшие типы точек покоя на плоскости
- •§5.3 Исследование на устойчивость по первому приближению
- •§5.4 Прямой (второй) метод Ляпунова
- •Глава 6. Уравнения с частными производными первого порядка.
- •§6.2. Решение однородных линейных уравнений
- •§6.3. Решение квазилинейных уравнений
- •§6.4. Решение задачи Коши для квазилинейных уравнений
§4.1. Решение однородных линейных систем с постоянными коэффициентами
Рассмотрим систему уравнений EMBED
Equation.3
![]() ,
где EMBED Equation.3
,
где EMBED Equation.3
![]() .
Будем искать решение в виде EMBED Equation.3
.
Будем искать решение в виде EMBED Equation.3
![]() .
Подставляем EMBED Equation.3
.
Подставляем EMBED Equation.3
![]() ,
EMBED Equation.3
,
EMBED Equation.3
![]() – собственный вектор, а
– собственное значение матрицы A.
Собственные значения – корни
характеристического (векового) уравнения
EMBED Equation.3
– собственный вектор, а
– собственное значение матрицы A.
Собственные значения – корни
характеристического (векового) уравнения
EMBED Equation.3
![]() .
Это алгебраическое уравнение относительно
степени n.
.
Это алгебраическое уравнение относительно
степени n.
Пусть уравнение EMBED Equation.3 имеет простые вещественные корни EMBED Equation.3
 .
Тогда матрица A имеет
простые собственные значения EMBED
Equation.3
.
Каждому EMBED Equation.3
.
Тогда матрица A имеет
простые собственные значения EMBED
Equation.3
.
Каждому EMBED Equation.3
 сопоставляем собственный вектор EMBED
Equation.3
сопоставляем собственный вектор EMBED
Equation.3
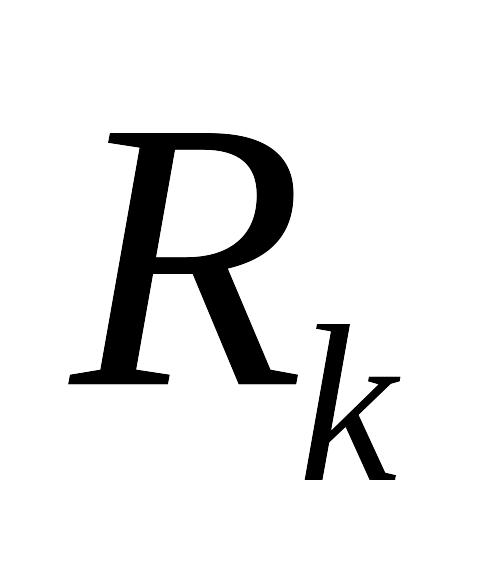 .
Имеем собственные векторы EMBED Equation.3
.
Имеем собственные векторы EMBED Equation.3
 .
Они линейно независимы. По формуле
EMBED Equation.3
.
Они линейно независимы. По формуле
EMBED Equation.3
 получаем решение системы EMBED Equation.3
получаем решение системы EMBED Equation.3
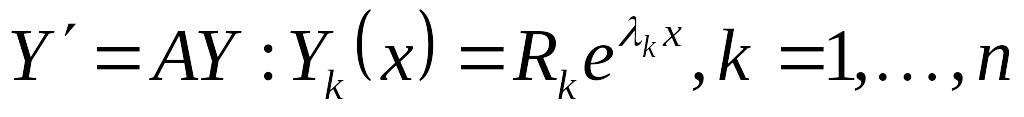 .
Эти решения линейно независимы (т.к.
определитель Вронского отличен от 0),
их n, следовательно,
они образуют ФСР. Общее решение системы
EMBED Equation.3
.
Эти решения линейно независимы (т.к.
определитель Вронского отличен от 0),
их n, следовательно,
они образуют ФСР. Общее решение системы
EMBED Equation.3
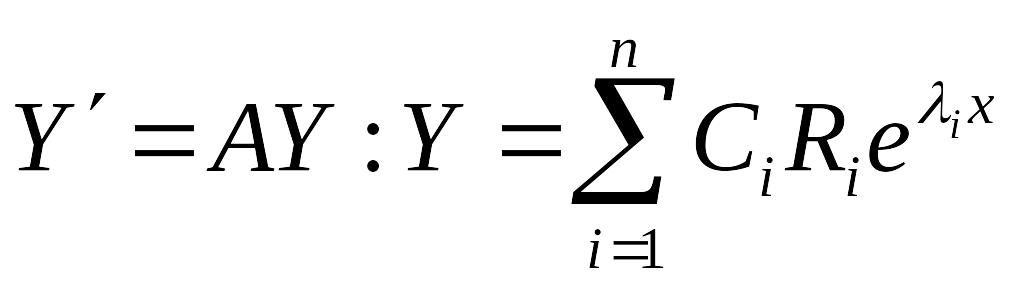 .
.Корни характеристического уравнения EMBED Equation.3 простые, но среди них есть комплексные. Пусть EMBED Equation.3 – корни уравнения EMBED Equation.3 . Они являются собственными значениями матрицы A. Пусть EMBED Equation.3 – какой-либо корень. Если он вещественный, то по формуле EMBED Equation.3 получаем решение: EMBED Equation.3
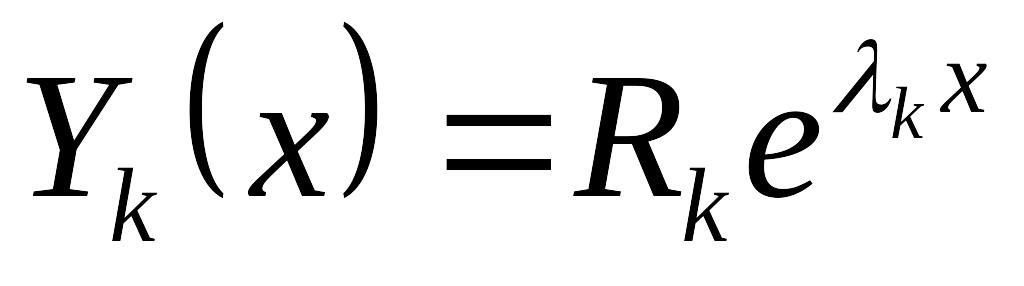 .
Пусть теперь EMBED Equation.3
– комплексный корень, EMBED Equation.3
.
Пусть теперь EMBED Equation.3
– комплексный корень, EMBED Equation.3
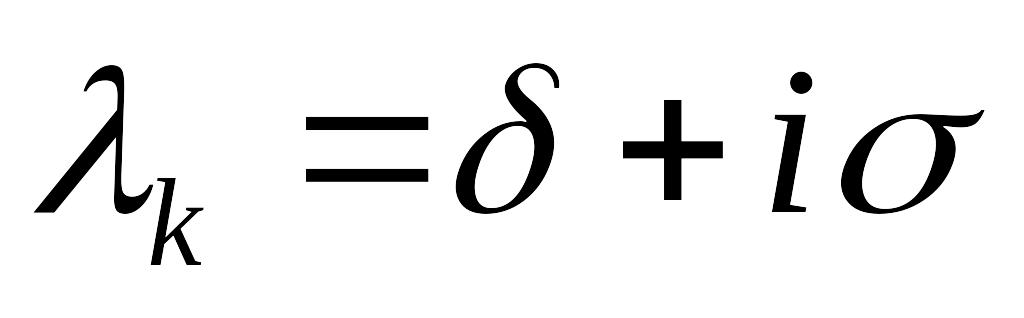 .
Тогда в силу вещественности матрицы A
существует ещё один корень EMBED Equation.3
.
Тогда в силу вещественности матрицы A
существует ещё один корень EMBED Equation.3
 .
Этим комплексным значениям соответствуют
комплексные собственные векторы EMBED
Equation.3
и EMBED Equation.3
.
Этим комплексным значениям соответствуют
комплексные собственные векторы EMBED
Equation.3
и EMBED Equation.3
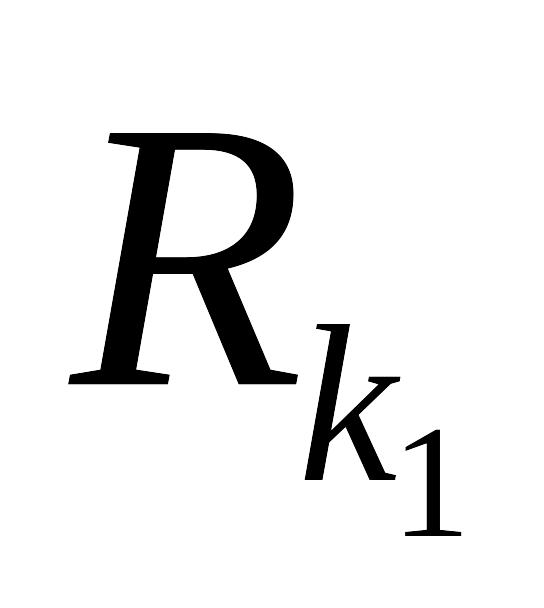 ,
причём EMBED Equation.3
,
причём EMBED Equation.3
 ,
следовательно, корням EMBED Equation.3
и EMBED Equation.3
,
следовательно, корням EMBED Equation.3
и EMBED Equation.3
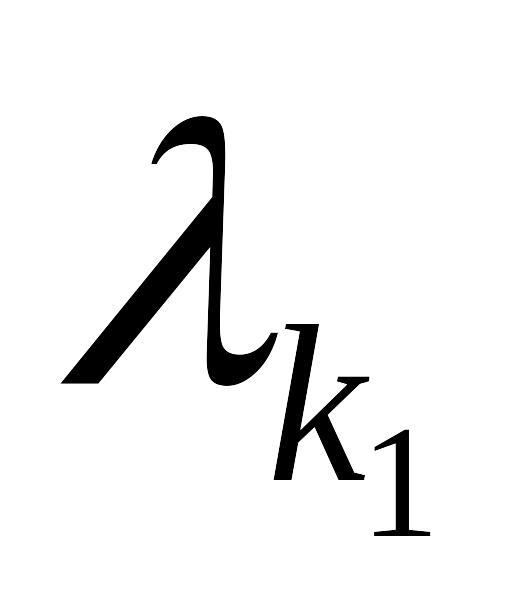 сопоставляется комплексные решения
EMBED Equation.3
сопоставляется комплексные решения
EMBED Equation.3
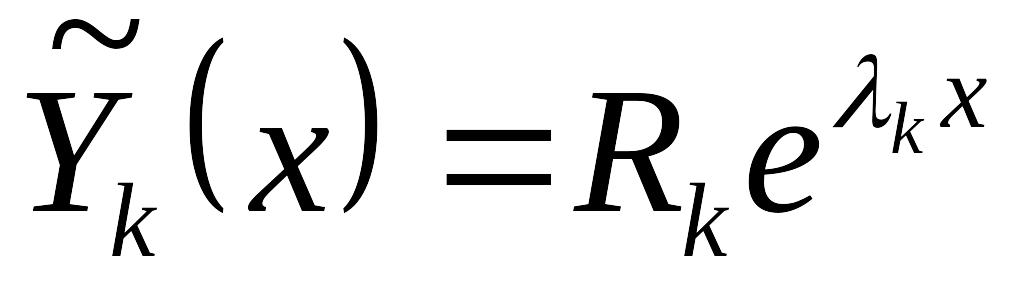 и EMBED Equation.3
и EMBED Equation.3
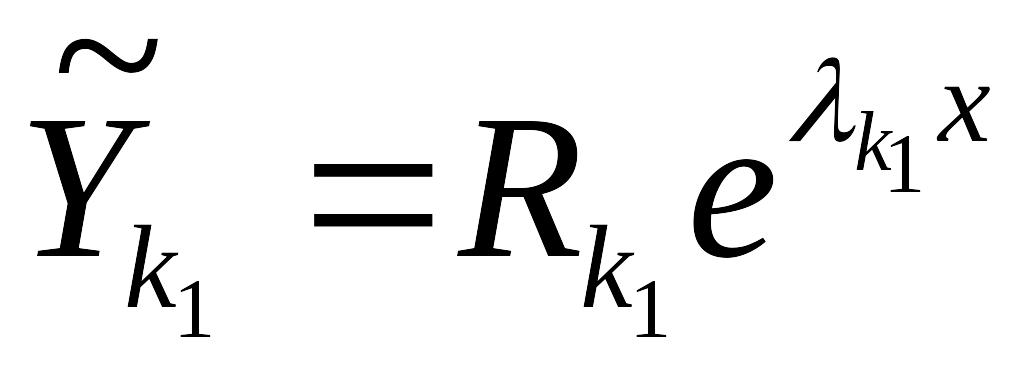 .
При этом EMBED Equation.3
.
При этом EMBED Equation.3
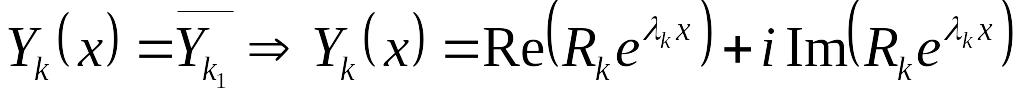 ,
EMBED Equation.3
,
EMBED Equation.3
 .
Выбираем EMBED Equation.3
.
Выбираем EMBED Equation.3
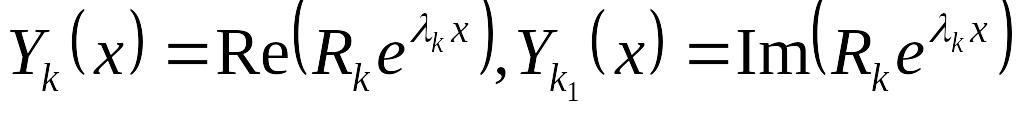 .
В итоге двум комплексным корням
поставлены в соответствие два вещественных
решения. Разбираясь таким образом с
каждым корнем уравнения EMBED Equation.3
,
получаем n решений.
Эти решения линейно независимы,
следовательно, они образуют ФСР,
следовательно, можно записать общее
решение системы EMBED Equation.3
.
.
В итоге двум комплексным корням
поставлены в соответствие два вещественных
решения. Разбираясь таким образом с
каждым корнем уравнения EMBED Equation.3
,
получаем n решений.
Эти решения линейно независимы,
следовательно, они образуют ФСР,
следовательно, можно записать общее
решение системы EMBED Equation.3
.Пусть уравнение EMBED Equation.3 имеет корни EMBED Equation.3
 ,
соответственно, кратности EMBED Equation.3
.
Имеем EMBED Equation.3
.
Если EMBED Equation.3
,
соответственно, кратности EMBED Equation.3
.
Имеем EMBED Equation.3
.
Если EMBED Equation.3
 ,
то все корни простые. Этот случай уже
рассмотрен. Пусть EMBED Equation.3
,
то все корни простые. Этот случай уже
рассмотрен. Пусть EMBED Equation.3
 ,
тогда существует хотя бы один корень
EMBED Equation.3
кратности EMBED Equation.3
,
тогда существует хотя бы один корень
EMBED Equation.3
кратности EMBED Equation.3
 .
По-прежнему сопоставляем каждому корню
решения системы EMBED Equation.3
,
число которых равно кратности корня.
Поскольку EMBED Equation.3
– кратный корень, ему можно сопоставить
по формуле EMBED Equation.3
в общем случае несколько решений EMBED
Equation.3
.
По-прежнему сопоставляем каждому корню
решения системы EMBED Equation.3
,
число которых равно кратности корня.
Поскольку EMBED Equation.3
– кратный корень, ему можно сопоставить
по формуле EMBED Equation.3
в общем случае несколько решений EMBED
Equation.3
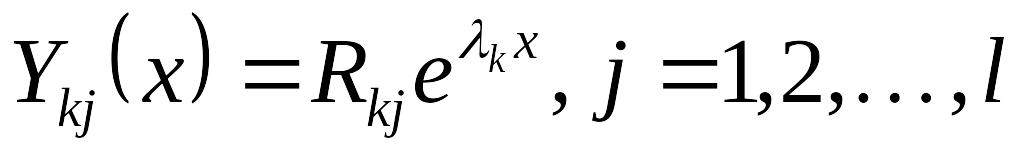 ,
где EMBED Equation.3
,
где EMBED Equation.3
 – линейно независимые собственные
векторы, соответствующие собственному
значению EMBED Equation.3
.
Если EMBED Equation.3
– линейно независимые собственные
векторы, соответствующие собственному
значению EMBED Equation.3
.
Если EMBED Equation.3
 ,
недостающие решения можно искать в
виде EMBED Equation.3
,
недостающие решения можно искать в
виде EMBED Equation.3
 ,
где EMBED Equation.3
,
где EMBED Equation.3
 – неопределённые постоянные векторные
коэффициенты (удобнее взять EMBED
Equation.3
– неопределённые постоянные векторные
коэффициенты (удобнее взять EMBED
Equation.3
 ).
Выбирая EMBED Equation.3
).
Выбирая EMBED Equation.3
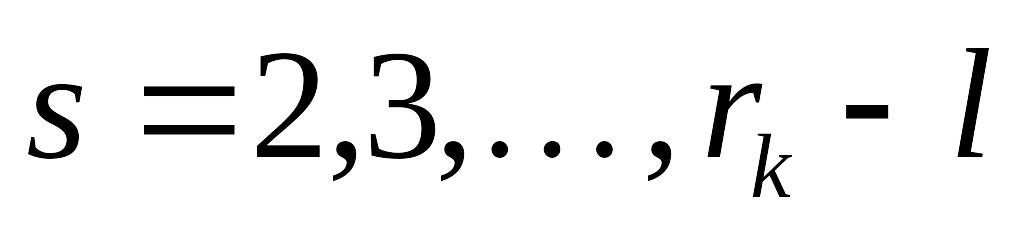 ,
достраиваем недостающие решения до
EMBED Equation.3
,
достраиваем недостающие решения до
EMBED Equation.3
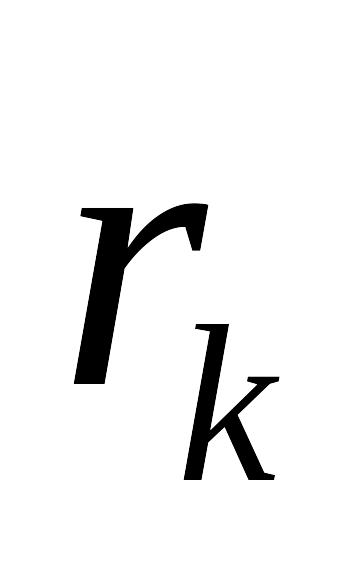 .
Поступая таким образом с каждым кратным
корнем, получаем n
решений системы EMBED Equation.3
.
В общем случае эти решения комплексные.
Выделяя вещественные и мнимые части у
построенных решений (как в пункте 2),
получаем n вещественных
решений системы EMBED Equation.3
.
Они линейно независимы, следовательно,
они образуют ФСР. Получаем общее решение
системы EMBED Equation.3
.
Отметим, что можно ограничиться и
выбором комплексной ФСР. В этом случае
при записи общего решения системы
произвольные постоянные также должны
быть комплексными.
.
Поступая таким образом с каждым кратным
корнем, получаем n
решений системы EMBED Equation.3
.
В общем случае эти решения комплексные.
Выделяя вещественные и мнимые части у
построенных решений (как в пункте 2),
получаем n вещественных
решений системы EMBED Equation.3
.
Они линейно независимы, следовательно,
они образуют ФСР. Получаем общее решение
системы EMBED Equation.3
.
Отметим, что можно ограничиться и
выбором комплексной ФСР. В этом случае
при записи общего решения системы
произвольные постоянные также должны
быть комплексными.
Можно предложить ещё один
способ решения систем уравнений с
постоянными коэффициентами. Он позволяет
решать и неоднородные системы EMBED
Equation.3
:
делаем замену EMBED Equation.3
![]() ,
где C
– невырожденная постоянная матрица.
EMBED Equation.3
,
где C
– невырожденная постоянная матрица.
EMBED Equation.3
![]() .
Выбираем C
таким, что EMBED Equation.3
.
Выбираем C
таким, что EMBED Equation.3
![]() – наиболее простая матрица, например,
диагональная.
– наиболее простая матрица, например,
диагональная.
Решения неоднородных линейных систем. Метод вариации постоянных. Матрица Коши.
Рассмотрим неоднородную систему EMBED Equation.3 .
Пусть EMBED Equation.3
– фундаментальные системы решений,
соответствующие системе EMBED Equation.3
![]() – частное решение системы EMBED Equation.3
.
Тогда EMBED Equation.3
– частное решение системы EMBED Equation.3
.
Тогда EMBED Equation.3
![]() – общие решения системы EMBED Equation.3
,
где EMBED Equation.3
– общие решения системы EMBED Equation.3
,
где EMBED Equation.3
![]() – произвольное постоянные.
– произвольное постоянные.
Общее решение неоднородной системы EMBED Equation.3 представляется суммой частного решения и общего решения соответствующей неоднородной системы.
Решить неоднородную систему EMBED Equation.3 можно, если подобрать какое-либо частное решение этой системы и решить соответствующую однородную систему. Если частное решение подобрать не удаётся, можно воспользоваться методом вариации произвольных постоянных.
Пусть уже построена ФСР соответствующей
однородной системы. Тогда её общее
решение имеет вид EMBED
Equation.3
![]() .
Полагая EMBED Equation.3
.
Полагая EMBED Equation.3
![]() ,
будем искать решения системы в виде
EMBED Equation.3
,
будем искать решения системы в виде
EMBED Equation.3
![]() :
EMBED Equation.3
:
EMBED Equation.3
![]() ,
т.к. EMBED Equation.3
,
т.к. EMBED Equation.3
![]() .
Введём матрицу EMBED Equation.3
.
Введём матрицу EMBED Equation.3
![]() составив её из всех столбцов EMBED
Equation.3
.
Тогда уравнение запишется в виде EMBED
Equation.3
составив её из всех столбцов EMBED
Equation.3
.
Тогда уравнение запишется в виде EMBED
Equation.3
 .
Заметим, что EMBED Equation.3
.
Заметим, что EMBED Equation.3
![]() при EMBED Equation.3
при EMBED Equation.3
![]() ,
следовательно, EMBED Equation.3
,
следовательно, EMBED Equation.3
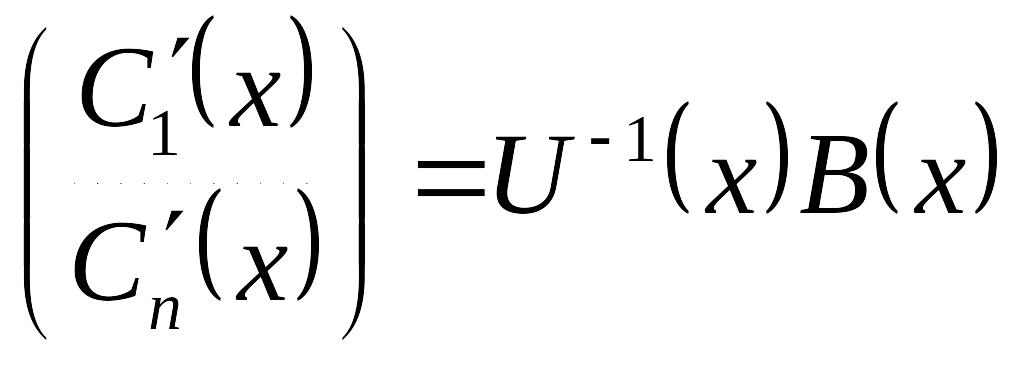 .
Интегрируя, получаем: EMBED Equation.3
.
Интегрируя, получаем: EMBED Equation.3
 ,
где EMBED Equation.3
,
где EMBED Equation.3
![]() .
Заметим, что формула EMBED Equation.3
.
Заметим, что формула EMBED Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() приводится к виду EMBED
Equation.3
приводится к виду EMBED
Equation.3
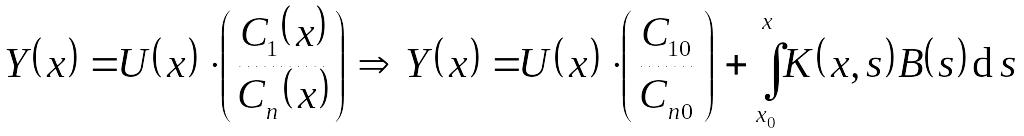 ,
где EMBED Equation.3
,
где EMBED Equation.3
![]() – матрица Коши. Здесь EMBED Equation.3
– матрица Коши. Здесь EMBED Equation.3
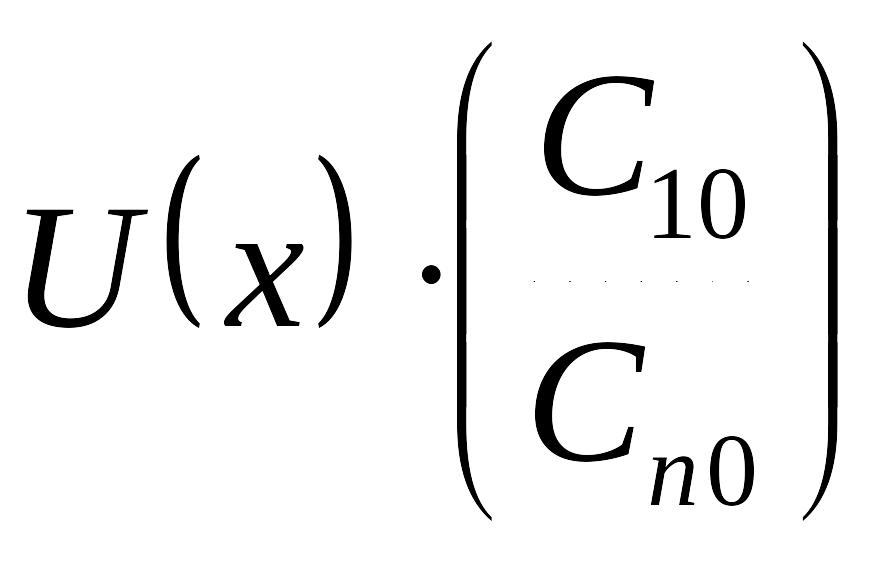 – общее решение соответствующей
однородной системы, а EMBED Equation.3
– общее решение соответствующей
однородной системы, а EMBED Equation.3
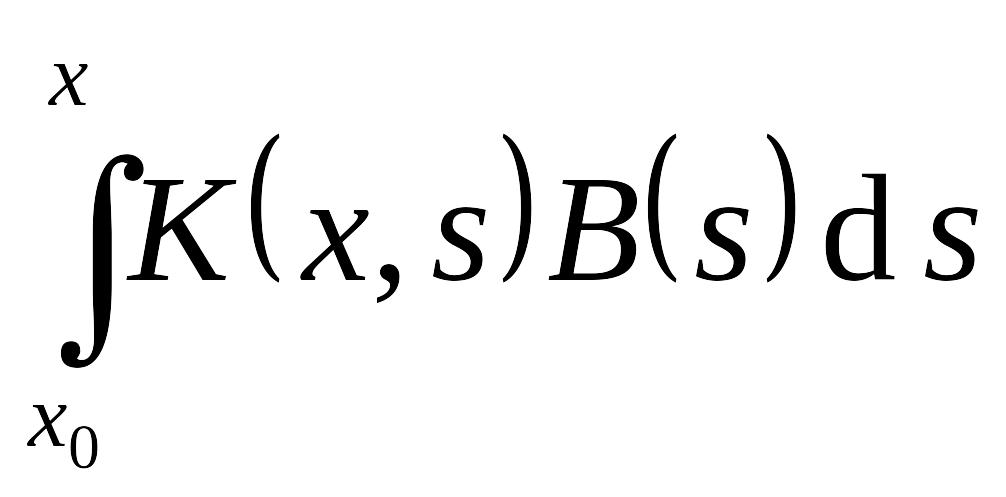 – частное решение неоднородной системы.
– частное решение неоднородной системы.
EMBED Equation.3
![]() .
При фиксированном s
матрицу Коши можно понимать как матричное
решение уравнения EMBED Equation.3
.
При фиксированном s
матрицу Коши можно понимать как матричное
решение уравнения EMBED Equation.3
![]() ,
удовлетворяющее начальному условию
EMBED Equation.3
,
удовлетворяющее начальному условию
EMBED Equation.3
![]() .
.
