Дифференциальные уравнения

Глава 0. Основные понятия теории дифференциальных уравнений

Под дифференциальным уравнением понимается соотношение типа равенства, содержащее подлежащую определению функцию и производные этой функции до некоторого порядка. Максимальный порядок производной, содержащейся в уравнении, называется порядком уравнения.

В случае одной независимой переменной дифференциальное уравнение называется обыкновенным дифференциальным уравнением (ОДУ).

В случае нескольких независимых переменных уравнение называется уравнением с частными производными (УЧП).

Функция, которая при подстановке в уравнение обращает уравнение в тождество, называют решением уравнения.

В общем случае решение дифференциального уравнения определяется неоднозначно, т.е. дифференциальное уравнение сопоставляет множество решений. Могут быть исключения, например уравнение имеет одно вещественное решение: .

Решить дифференциальное уравнение значит найти (описать) все решения этого уравнения. Обычно при решении дифференциального уравнения ставят целью получение общего решения. Так, для уравнения – общее решение. Здесь C – произвольная постоянная. Других решений этого уравнения нет. Однако, такое возможно не всегда. Так, уравнение EMBED Equation.3 имеет общее решение EMBED Equation.3 . Однако существует ещё одно решение EMBED Equation.3 . Его не удаётся включить в общее решение. Такие решения называются особыми.

Основное внимание в этом курсе уделяется обыкновенным дифференциальным уравнениям (ОДУ). В общем случае ОДУ представляется в виде EMBED Equation.3 – ОДУ n-го порядка. Решение таких уравнений понимается в классическом смысле: непрерывно дифференцируемая функция до порядка n, при подстановке обращающая уравнение в тождество. Геометрически решению EMBED Equation.3 на плоскости xy соответствует линия, называемая интегральной.

Обычно при решении прикладных задач уравнение рассматривается вместе с некоторыми дополнительными условиями. В этом случае говорят, что рассматривается задача. Простейшие дополнительные условия: условия Коши (начальные), которые задают задачу Коши; и краевые условия, дающие краевую задачу.

Примеры: EMBED Equation.3 – задача Коши, EMBED Equation.3 – краевая задача.

Глава 1. Уравнения первого порядка.

§ 1.1 Уравнения, разрешённые относительно производных; их геометрическая интерпретация.

Рассмотрим уравнение 1-го порядка вида EMBED Equation.3 , предполагая, что функция EMBED Equation.3 определена в некоторой области EMBED Equation.3 . Область D – область определения уравнения. Чаще всего EMBED Equation.3 предполагается непрерывной в D. Решением EMBED Equation.3 называется функция EMBED Equation.3 , непрерывная и непрерывно дифференцируемая, для которой EMBED Equation.3 и EMBED Equation.3 . Здесь x пробегает некоторое множество. Если рассматривается EMBED Equation.3 , то говорят, что EMBED Equation.3 – решение уравнения EMBED Equation.3 на EMBED Equation.3 .

Общим решением уравнения EMBED Equation.3 в области D называется функция EMBED Equation.3 , удовлетворяющая условиям:

1. Для любой точки EMBED Equation.3 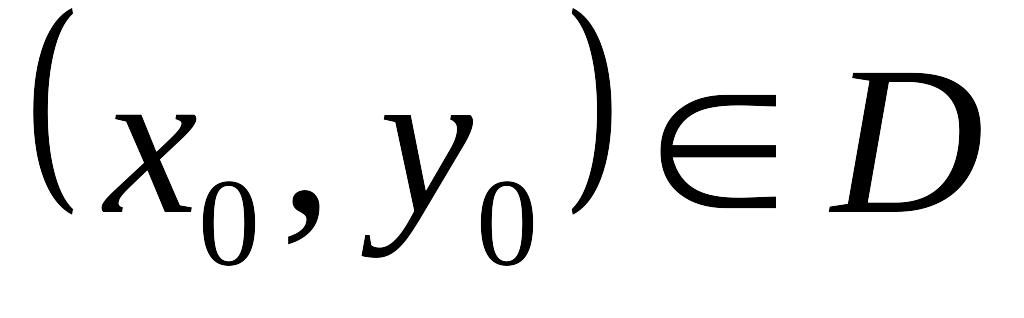уравнение EMBED Equation.3 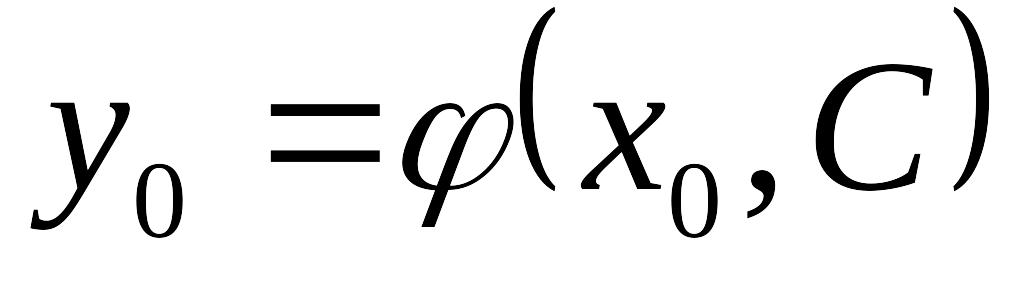однозначно определяет EMBED Equation.3 .

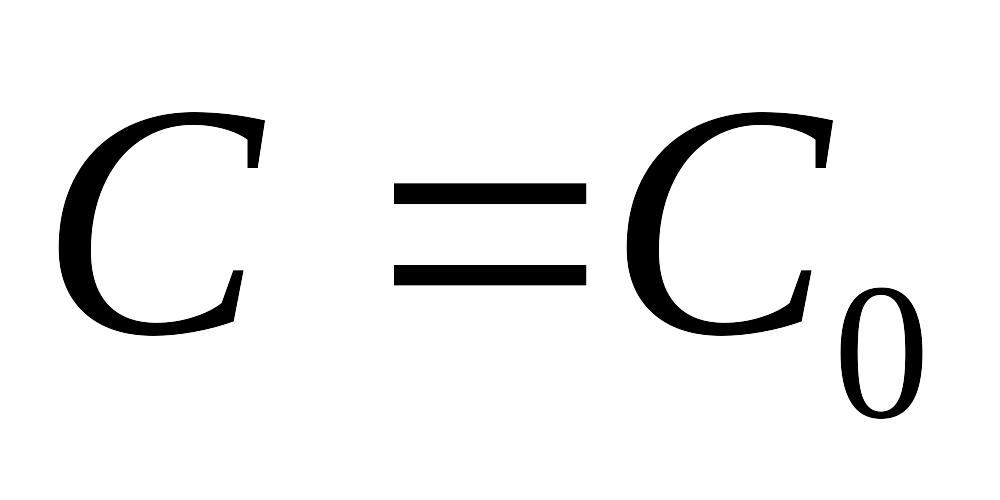2. Функция EMBED Equation.3 является решением уравнения EMBED Equation.3 .

Решение уравнения EMBED Equation.3 , получающееся из общего решения при конкретном задании постоянной C называется частным решением уравнения.

Решение, не являющееся частным решением, называется особым решением.

Геометрически решению уравнения EMBED Equation.3 отвечает интегральная линия на плоскости xy (график функции EMBED Equation.3 ), а общему решению – семейство интегральных линий. Заметим, что через любую точку в области EMBED Equation.3 проходит единственная интегральная линия из этого семейства.

Для уравнения EMBED Equation.3 можно поставить дополнительные условия: найти интегральную линию, проходящую через дополнительную точку EMBED Equation.3 . Получается начальное условие: EMBED Equation.3 . Имеем задачу Коши. Решить задачу Коши значит среди всех интегральных линий уравнения найти ту, которая проходит через данную точку EMBED Equation.3 .

Уравнение EMBED Equation.3 в области D задаёт векторное поле (поле касательных направлений).

Геометрически решить уравнение EMBED Equation.3 – это провести линии в области D так, чтобы в каждой точке такой линии касательная определялась векторным полем.

Изоклина – геометрическое место точек, в каждой точке которых векторы равны.

В дальнейшем будем считать, что переменные x и y в уравнении EMBED Equation.3 равноправны. В случае, когда EMBED Equation.3 установится неограниченным, можно рассматривать уравнение EMBED Equation.3 . Будем также записывать уравнение в виде EMBED Equation.3 , где EMBED Equation.3 в D.

Часто не удаётся получить решение уравнения EMBED Equation.3 в явном виде. Если решение удаётся получить в неявном виде – EMBED Equation.3 , – то такое конечное уравнение называется интегралом уравнения EMBED Equation.3 . Если в неявном виде получается общее решение уравнения EMBED Equation.3 , то имеем общий интеграл уравнения EMBED Equation.3 .