2. Влияние последействия отказов элементов

на надежность системы

1. Постановка задачи

Дано:

• структурная схема технической системы (система 1);

• λ – интенсивность отказов элементов до отказа какого-нибудь одно из них;

• λ' – интенсивность отказов элементов после отказа любого одного элемента;

• дублированная система с постоянно включенным резервом (система 2);

• вид закона распределения времени до отказа элементов системы 2, отличный от экспоненциального;

• математическое ожидание и среднее квадратическое отклонение времени безотказной работы элементов:

• до отказа m, σ любого элемента;

• после отказа m', σ' любого элемента;

• время работы систем t.

Определить:

• вероятность безотказной работы системы 1 при отсутствии и при наличии последействия отказов P_c(t), P_{c, посл}(t) в виде формул, таблиц и графиков;

• среднее время безотказной работы системы при отсутствии и при наличии последействия отказов: Т_c, Т_{c, посл};

• вероятность безотказной работы дублированной системы (система 2) при отсутствии и при наличии последействия отказов P_дc(t), P_{дc, посл}(t);

• среднее время безотказной работы дублированной системы при отсутствии и при наличии последействия отказов: Т_дc, Т_{дc, посл}.

Варианты заданий приведены в разд. 8.2.4.

2. Сведения из теории

Практически в любой технической системе отказы одних элементов приводят к увеличению нагрузки на остальные элементы. В результате интенсивности отказов работающих элементов возрастают. Этот эффект носит название “последействие” отказов. Любая техническая система в той или иной степени подвержена этому явлению.

Экспоненциальные распределения времени до отказа

Расчет надежности систем с последействием, элементы которых имеют экспоненциальные распределения времени до отказа, изменяется незначительно по сравнению с расчетом надежности систем без последействия.

Общий подход к анализу надежности таких систем состоит в следующем:

• описание функционирования системы графом состояний;

• составление по графу системы алгебраических уравнений относительно среднего времени пребывания системы τ_i в каждом исправном состоянии, решение системы и определение среднего времени безотказной работы: 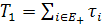, где Е₊ - множество исправных состояний;

• составление по графу системы дифференциальных уравнений относительно вероятностей пребывания системы р_i(t) в исправных состояниях, решение системы и определение вероятности безотказной работы:

.

Произвольные распределения времени до отказа

Проведем анализ надежности системы с последействием отказов, если элементы имеют неэкспоненциальные законы распределения времени до отказа. Покажем, что и в этом случае при вычислении показателей надежности системы эффект последействия можно учесть.

Рассмотрим дублированную систему с постоянно включенным резервом. Введем следующие обозначения:

• f₁(t) и P₁(t) – плотность распределения времени до отказа и вероятность безотказной работы элемента 1;

• f₂(t) и P₂(t) – плотность распределения времени до отказа и вероятность безотказной работы элемента 2;

• f₃(t) и P₃(t) – плотность распределения времени до отказа и вероятность безотказной работы элемента 1 после отказа элемента 2;

• f₄(t) и P₄(t) – плотность распределения времени до отказа и вероятность безотказной работы элемента 2 после отказа элемента 1.

Определим закон распределения времени до отказа системы. По формуле полной вероятности получим:

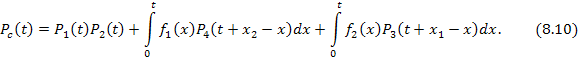
Появление параметра сдвига в аргументе функции обусловлено тем, что элемент 2 уже проработал время , и теперь до отказа он должен проработать время , но с законом распределения , причем не с самого начала, а с момента времени , обеспечивающего продолжение функционирования элемента 2. Момент времени берется так, чтобы вероятность остаточного времени работы элемента 2 после момента была одинаковой для законов и . Это значит, что должно выполняться равенство (условие сохранения остаточного ресурса). Таким образом, момент времени в формуле (8.10) является функцией момента . Аналогичный смысл имеет аргумент в функции , который определяется уравнением .

Рассмотрим частный случай экспоненциальных законов распределения, когда

По формуле (8.10) получим:

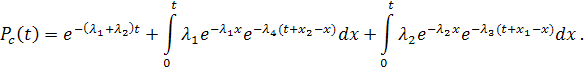
Из соотношения следует, что , а их соотношения − что . Следовательно:

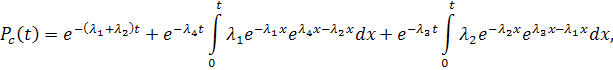
Для одинаковых по надежности элементов с первоначальной интенсивностью отказа λ и интенсивностью отказа λ' после возникновения отказа другого элемента получим:

Для неэкспоненциальных распределений расчет по формуле (8.10) является более сложной вычислительной задачей.

Если элементы дублированной системы имеют одинаковую надежность, то

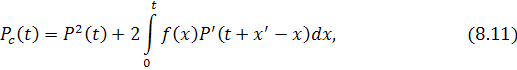
где:

• f(t) и P(t) – плотность распределения и вероятность безотказной работы элемента до наступления отказа другого элемента;

• P'(t) – вероятность безотказной работы после отказа другого элемента;

• x' – корень уравнения P'(x') = P(x).

Исследование надежности дублированной системы с последействием отказов элементов можно провести на основе программного средства aftereffect.exe, рассчитывающего вероятность безотказной работы в соответствии с формулами (8.10) или (8.11). Описание программы содержится в части IV.

В [5, разд. 8.7] получены вероятности безотказной работы дублированной системы с последействием отказов для случаев отсутствия и наличия “памяти”. Приведем соответствующие формулы:

• отсутствие “памяти”. Вероятность безотказной работы системы выражается формулой:

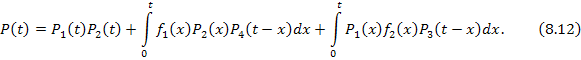
В частности, если элементы равнонадежны, то

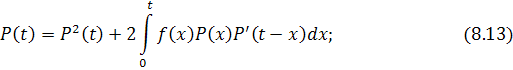
• наличие “памяти”. Вероятность безотказной работы системы выражается формулой:

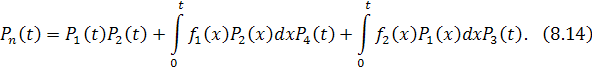
В частности, если элементы равнонадежны, то

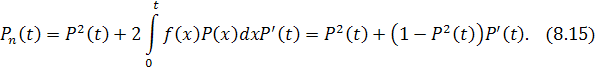
Покажем, что выражения (8.12) и (8.14) являются соответственно нижней и верхней оценками вероятности безотказной работы системы, вычисленной по формуле (8.10).

Для этого сделаем два естественных допущения:

• распределения 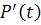− “стареющие”, т.е. вероятность остаточного времени “жизни” элемента в течение времени x не превышает вероятности безотказной работы за это же время:

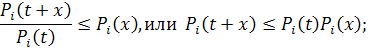
• эффект последействия может только ухудшить показатели надежности элементов:

В силу первого допущения:

и, значит:

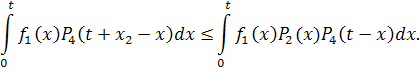
Отсюда следует, что .

Согласно второму допущению, , и в силу убывания функции , получим . Тогда:

значит:

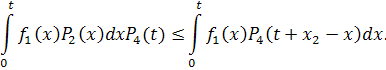
Отсюда следует, что .

Таким образом, получена двусторонняя оценка вероятности безотказной работы системы с последействием отказов:

. (8.16)

В [5, разд. 8.7] получены формулы для вероятности безотказной работы резервированной системы кратности n−1 с последействием отказов для случаев отсутствия и наличия “памяти”:

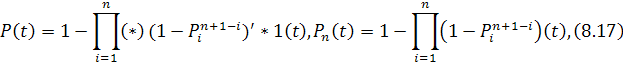
где – плотность распределения времени безотказной работы, а – вероятность безотказной работы каждого элемента после отказа i элементов, i = 0,1,2,…,n−1.

Соотношения (8.17) являются обобщением формул (8.13) и (8.15) на системы с произвольным числом элементов. Они имеют простой смысл. Вероятности и равны вероятностям безотказной работы схем общего резервирования замещением (рис. 8.5, а) и с постоянным резервом (рис. 8.5, б). Элементы каждой нерезервированной подсистемы равнонадежны, а элементы различных подсистем имеют разную надежность.

Рис. 8.5. Структурные схемы систем с последействием отказов

для случаев отсутствия (а) и наличия (б) “памяти”

Время до отказа системы в случае отсутствия “памяти”

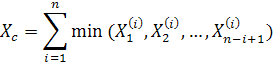
соответствует резервированию замещением, а в случае наличия “памяти”

− резервированию с постоянным резервом. Отсюда, в частности, следует неравенство .