3. Последовательность выполнения работы

Лабораторную работу целесообразно выполнять в такой последовательности:

1. Определить наработку на отказ системы.

2. Исследовать функцию и коэффициент готовности системы.

3. Выполнить анализ риска системы.

Отчет о лабораторной работе должен содержать следующие пункты:

1. Постановка задачи.

2. Уравнения и расчетные формулы.

3. Таблицы и графики.

4. Выводы по каждому пункту и по результатам работы в целом.

4. Пример выполнения лабораторной работы

Пусть нерезервированная система имеет следующие исходные данные:

• число элементов системы n = 10;

• время жизни (долговечность) системы T_n = 1000 час;

• допустимый риск системы R ≤ 2500 усл. ед.;

• значения риска, интенсивностей отказов и восстановления элементов системы приведены в табл. 5.1.

Таблица 5.1. Исходные данные задачи

Номера элементов	1	2	3	4	5	6	7	8	9	10
λ∙10-4, час-1	1	0,23	0,36	0,054	0,72	0,83	0,08	0,25	0,6	1,2
r, усл. ед.	20	50	40	104	600	250	103	10	80	100
μ∙10-1, час-1	0,2	0,3	0,5	2	1	1,2	7	0,5	1	1

1. Определение наработки на отказ системы

Определим интенсивность отказа системы. Суммирование интенсивностей отказов элементов с помощью пакета Derive 5 н6аиболее просто и удобно выполнить с помощью функции ELEMENT и кнопки Sum панели инструментов, предварительно образовав вектор элементов i, i = 1, 2, …, n. Подробно этот способ был описан в лабораторной работе 2. В результате вычислений получим час^-1. Тогда на основании формулы (5.4) наработка на отказ будет равна .

2. Исследование функции и коэффициента готовности системы

Определить коэффициент готовности с помощью системы Derive 5 наиболее просто следующими способами:

• образовать вектор значений …, 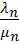с помощью кнопки Author Vector, при этом операцию деления нужно только обозначить, но вычисления не делать;

• вычислить значения суммы элементов вектора с помощью кнопки Find Sum панели инструментов;

• вычислить К_г = 1/(1 + #k), где #k – номер выражения суммы.

Для исходных данных нашей задачи получаем:

или

Значения коэффициента готовности, вычисленные по формулам (5.2) и (5.3), полностью совпадают.

Функцию готовности определим двумя способами.

Способ 1. Решим систему дифференциальных уравнений (5.6) методом Рунге−Кутты с помощью Derive в такой последовательности:

• установить режим ввода переменных с индексами, выбрав пункт главного меню Declare │Input и щелкнув мышью на вкладке Word;

• ввести уравнения системы (5.6) в аналитическом виде;

• подставить в уравнения численные значения λ_i и μ_i с помощью команды Variable Substitution (кнопка Sub); на экране отобразятся 11 уравнений, не объединенных в систему;

• вызвать утилиту решения дифференциальных уравнений методом Рунге−Кутты: пункт меню File│Load│Utility File;

• ввести имя утилиты: ODE_APPR.MTH;

• набрать и ввести выражение функции решения дифференциальных уравнений методом Рунге−Кутты:

RK([#1,#2,#3,#4,#5,#6,#7,#8,#9,#10,#11], [t,p0,p1,p2,p3,p4,p5,p6,p7, p8, p9, p10], [0,1,0,0,0,0,0,0,0,0,0,0], 1, 500).

В первых квадратных скобках записаны номера, которые присвоены уравнениям на экране монитора. Во вторых квадратных скобках перечислены аргумент t и все искомые вероятности. В третьих квадратных скобках указаны начальные условия, за начальными условиями указывается шаг интегрирования (в нашем случае h = 1) и конечное значение аргумента t (в нашем случае 500).

В нашем примере состояние (0) соответствует исправному состоянию систему (см. рис. 5.1). Тогда К_г(t) = p₀(t), а К_г = .

Описанные ранее процедуры на экране монитора имеют вид:

В табл. 5.2 приведены результаты решения задачи при шаге интегрирования h = 0,5 и конечном значении аргумента, равном пяти (третий столбец таблицы).

Способ 2. Будем рассматривать нерезервированную систему как один элемент, имеющий интенсивность отказа λ_с и интенсивность восстановления μ_с. Тогда справедлива система дифференциальных уравнений (5.7), решением которой является функция (5.1). Для сравнения результатов расчетов двумя способами представим К_г(t) в виде таблицы. Решение легко получить, табулируя (5.1) с помощью функции

VECTOR([t, К_г(t)], tn, tk, dt).

В нашем случае tn = 0, tk = 5, dt = 0,5. Результаты табулирования приведены в табл. 5.2 (второй столбец таблицы). Из анализа данных следуют два важных вывода:

• оба способа вычисления функции готовности в данном примере дали практически одинаковые результаты;

• приближенная формула (5.1) дает несколько заниженные значения К_г(t) и является ее нижней оценкой.

Таблица 5.2. Функция готовности системы

t, час	Кг(t), прибл.	Кг(t), Рунге−Кутты
0	1	1
0,5	0,99737	0,99739
1	0,994825	0,994915
1,5	0,992347	0,992538
2	0,989939	0,990263
2,5	0,987599	0,988083
3	0,985325	0,985991
3,5	0,98311	0,98398
4	0,980969	0,982057
4,5	0,978882	0,980205
5	0,976855	0,978425

Таблица 5.3. Оценка длительности переходного процессе системы

t, час	Кг(t), прибл.	Кг(t), Рунге−Кутты
0	1	1
10	0,95947	0,96387
20	0,93664	0,946047
30	0,923766	0,935725
40	0,916510	0,928954
50	0,912420	0,924133
60	0,910115	0,920533
70	0,90881	0,91776
80	0,908084	0,915615
90	0,907671	0,913918
100	0,907438	0,912574

Определим теперь длительность переходного режима системы. Для этого увеличим диапазон табулирования функции (5.1), выбрав tn = 0, tk = 100, dt = 10. Данные табулирования приведены в табл. 5.3.

В третьем столбце таблицы приведены данные решения дифференциальных уравнений методом Рунге−Кутты. Из табл. 5.3 видно, что переходный процесс в системе длится короткое время. Так, например, в течение 100 часов работы системы функция готовности совпадает с коэффициентом готовности с точностью три знака после запятой. При t = Т = 188 час. функция и коэффициент готовности совпадают с точностью пять знаков после запятой. Из этих исследований вытекает важный для практики вывод: в течение времени t, равного наработке на отказ, переходный режим функционирования восстанавливаемой системы заканчивается и функция готовности практически совпадает с коэффициентом готовности.