1. Определение показателей надежности системы

Интенсивность отказов системы равна . Подставляя в это выражение значения интенсивностей отказов элементов из табл. 2.1, получим: λ₀ = 8,24^.10^-5 час^-1 (технология вычисления λ_с с помощью системы Derive 5 приведена далее в разд. 2.4.2).

Тогда вероятность и среднее время безотказной работы будут равны:

При t = T = 1000 час

2. Определение риска системы по точной формуле

Для образования вектора интенсивностей отказов и вектора риска r в системе Derive 5 необходимо выполнить следующие действия:

• выбрать пункт меню Author│Vector, на экране появится окно Vector Setup;

• ввести размер вектора (в нашем случае 10), нажать кнопку ОК, на экране появится окно ввода элементов вектора Author 10 element vector;

• ввести интенсивности отказов элементов (для ускорения процедуры ввода значения λ не умножаются на 10^-5), после нажатия кнопки ОК на экране в строке #1 отобразится вектор интенсивностей отказов элементов.

Аналогично образуется вектор риска r. Пусть он находится в строке #2.

Вычисление интенсивности отказов системы λ_с осуществляется с помощью следующих действий:

• набрать в строке пользователя функцию:

ELEMENT (#1, n),

после нажатия клавиши <Enter> на экране появится функция ELEMENT с вектором интенсивности отказов;

Внимание

В функции ELEMENT первым аргументом должен быть номер строки с вектором λ, определенным ранее, а вторым аргументом – символ n, а не его численное значение.

• щелкнуть на кнопке Find Sum панели инструментов, на экране появится новое окно Calculus Sum. На вкладке Variable установить значение n, на вкладке Sum установить переключатель в положение Definite, на вкладке Definite Sum определить область суммирования (в нашем случае от 1 (Lower Limit) до 10 (Upper Limit)). После нажатия ОК на экране отобразится выражение суммы элементов вектора λ_с;

• нажать кнопку Approximate панели инструментов, на экране появится искомое значение суммы интенсивностей отказов элементов. В нашем случае с учетом масштаба (10^-5) λ_с = 8,24∙10^-5 час^-1.

Для вычисления суммы необходимо получить скалярное произведение векторов λ и r, которые в нашем примере находятся соответственно под номерами #1 и #2. Для этого в строке пользователя набирается выражение #1 #2, нажимаются клавиша <Enter> и кнопка Approximate панели инструментов, на экране появляется ответ 1,0506 ∙10⁴. В нашем случае с учетом масштаба интенсивностей отказа (10^-5) искомая сумма равна 0,10506.

Процедуры решения на экране монитора имеют следующий вид:

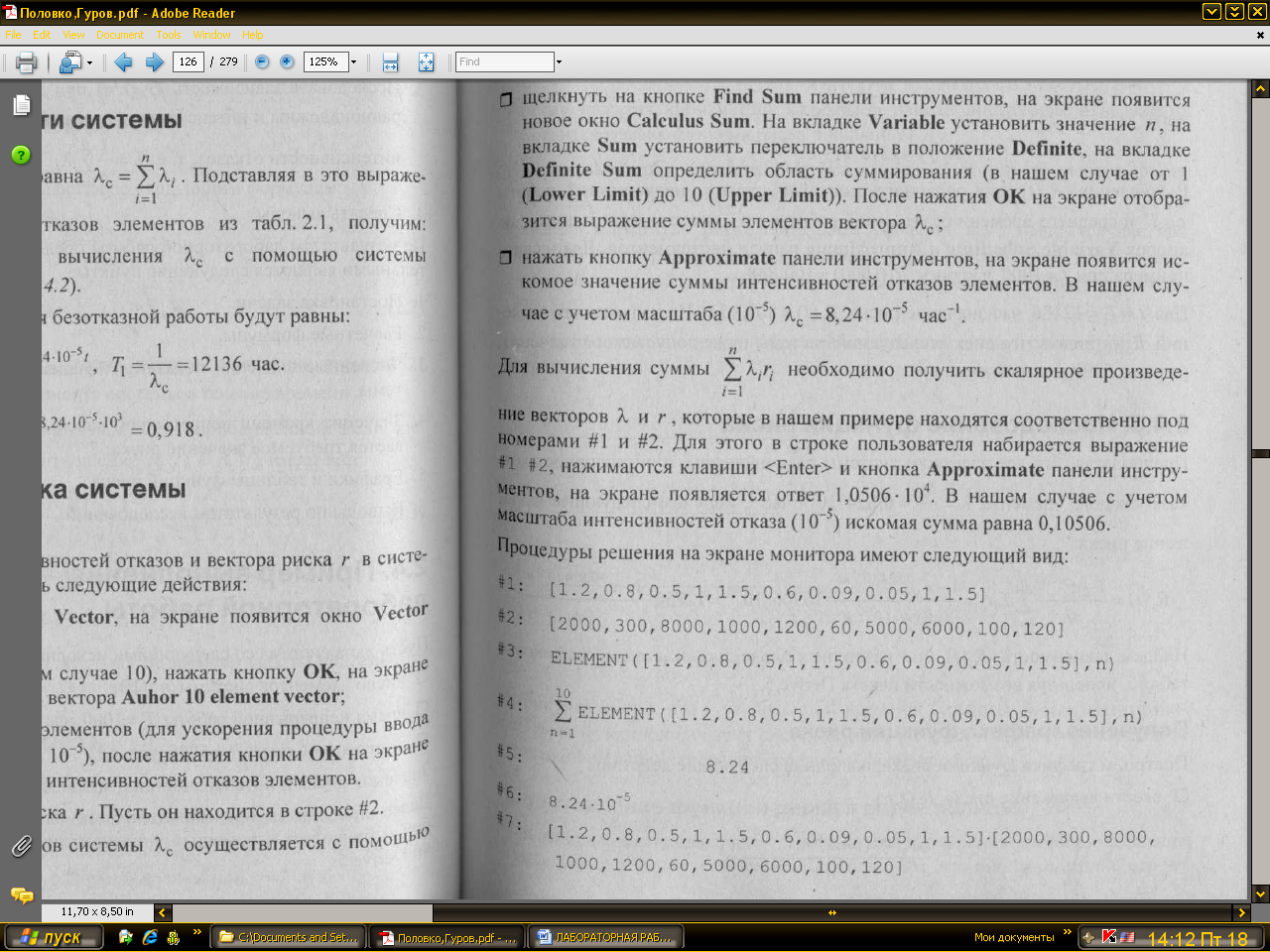
Так как Q_c(t) = 1−P_c(t) = 1− , λ_с = 8,24∙10^-5 , , то в соответствии с (2.1) функция риска будет равна:

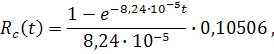
или

Вычисление R_c(t) для заданного значения времени непрерывной работы t = T и среднего времени безотказной работы t = T₁ выполняется с помощью кнопок Variable Substitute и Approximate панели инструментов. Для нашего примера при t = 1000 час риск R_c(1000) = 100,848.

Для t = T₁ = 12136 час значение риска R_c(t) = 805,953. Из полученных значений R_c(t) видно, что риск исследуемой системы ниже допустимого значения, равного 5000 условных единиц.