Алгоритм вычисления двойного интеграла
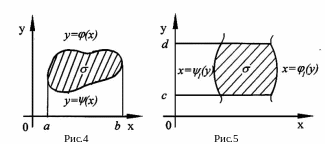
Область на плоскости
назовем простой
областью:
1) (относительно
оси
)
если она ограничена сверху линией
,
снизу
(функции
и
непрерывны)
и с боков отрезками прямых
и
(рис. 4); в частных случаях один из этих
отрезков (или оба вместе) могут превратиться
в точку (рис.5);
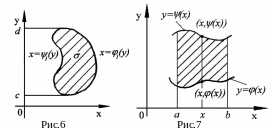
2) (относительно
оси
)
если она ограничена слева линией
,
справа
(функции
и
непрерывны) и сверху и снизу отрезками
прямых
и
(рис. 6, 7).
Тогда имеет место формула перехода от двойного интеграла к повторному
, (3.8)
где
-простая
область относительно оси
;
,
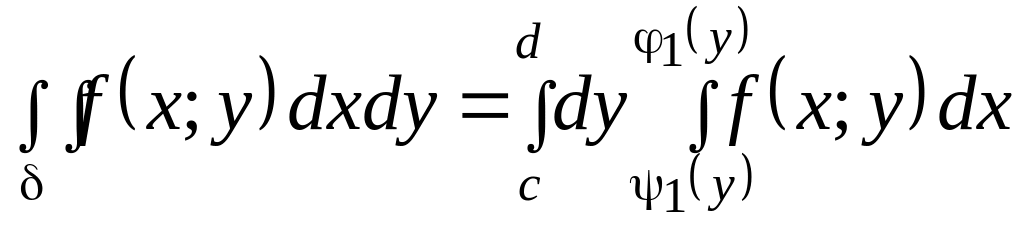(3.9)
где -простая область относительно оси .
З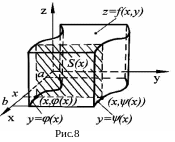
аметим,
что в случае вычисления объема
цилиндрических тел интеграл
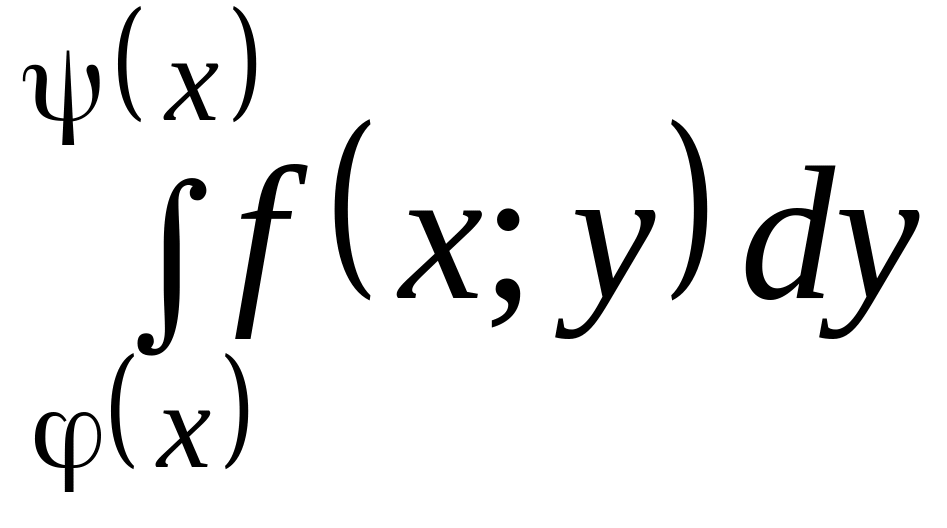дает площадь
поперечного сечения нашего тела (рис.8),
следовательно, весь объем
будет
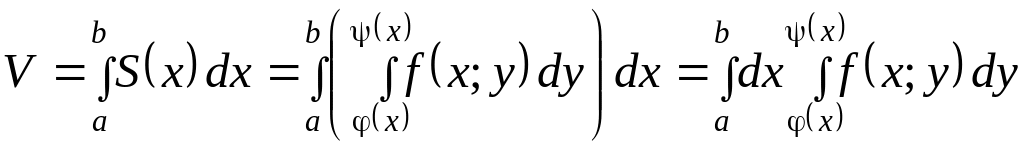(3.10)
Используя формулы
(3.2) и (3.7) получим формулу для вычисления
массы материальной двумерной пластинки
,
если известна её плотность
(3.11)
Наиболее
простой вид формулы (3.8) и (3.9) принимают
в случае прямоугольной области
,
ограниченной прямыми
,
,
,
(рис.9):
.
(3.12)
Следует заметить,
что если область
не является простой областью, то ее
разбивают на конечное число простых
областей
,
,
…,
и при вычислении двойного интеграла по
области
используют третье свойство двойного
интеграла.
О бразцы решения задач
Пример 1.
Вычислить двойной интеграл
,
если область
ограничена параболами
и
(рис.10).
Решение. Область
( см. рис.10) – простая (вида 1). Она ограничена
снизу кривой
,
сверху – кривой
,
т.е.
или
(перед радикалом ставим только знак
“+”, так как область
находится в I
квадранте, где
);
при любом фиксированном значении
из отрезка
меняется от
до
.
Поэтому по формуле (3.9) при
имеем
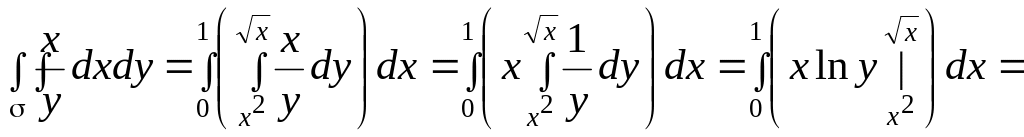
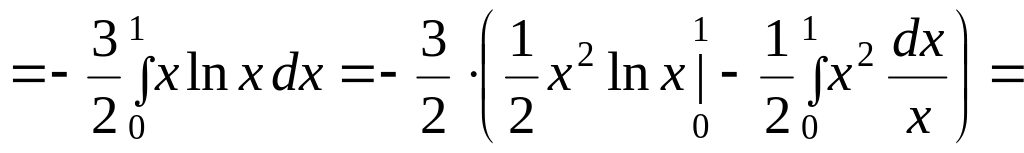
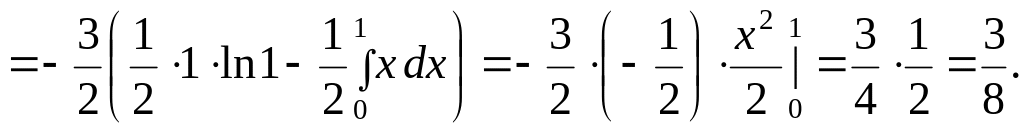
Замечание
Интеграл
взят методом интегрирования по частям,
причем при подстановке нижнего предела
использовался тот факт, что
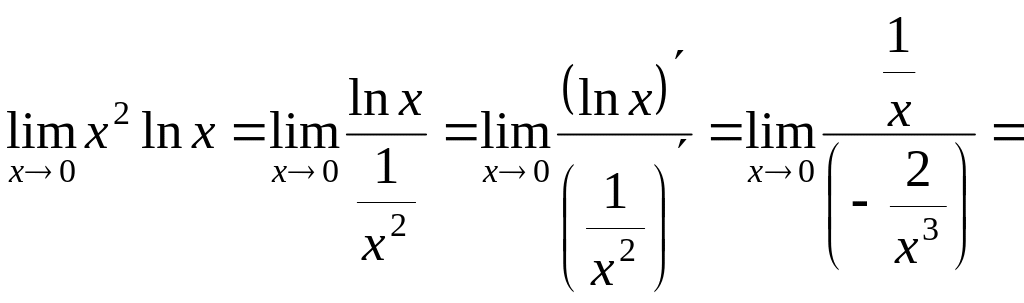
Пример
2. Вычислить
двойной интеграл
,
если область
ограничена слева кривой
,
справа прямой
и с боков прямыми
,
.
Решение.
Область
(рис.11) является простой (вида 2). При
любом фиксированном
из отрезка
меняется от
,
до
.
Поэтому по формуле (3.8) имеем:
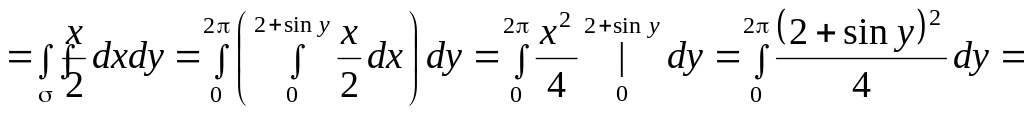
Замечание.
Интеграл
взят методом подстановки
,
тогда
или
.
При изменении
от 0 до
t
меняется от 0 до
.
Следовательно,
.
Пример
3. Вычисляется
объем цилиндрического тела, ограниченного
снизу областью
,
указанной на рис.12, и сверху – плоскостью
.
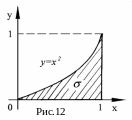Решение.
Область интегрирования
ограничена снизу кривой
,
сверху – кривой
.
Спроецировав
на ось
,
получим отрезок
.
Следовательно,
.
По формуле (3.10) при
имеем:
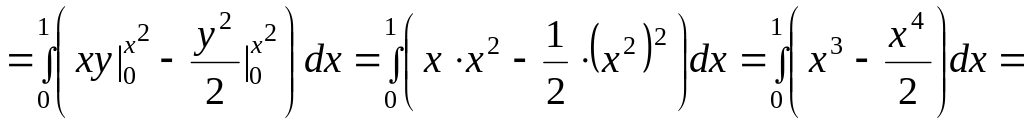
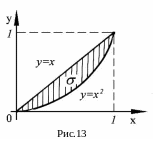Пример
4. Вычислить
массу пластинки, ограниченной прямой
и параболой
(рис.13), если плотность распределения
массы выражается функцией
.
Решение.
Область интегрирования
ограничена снизу кривой
,
сверху – кривой
,
спроецировав,
на
ось
,
получим отрезок
.
Следовательно,
.
По формуле (3.11) при
имеем:
