
- •Введение
- •Лабораторная работа 1
- •Примеры решения задач
- •Лабораторная работа 2
- •Лабораторная работа 3
- •Примеры решения задач
- •Задания лабораторной работы
- •Лабораторная работа 4
- •Примеры решения задач
- •Лабораторная работа 5
- •Примеры решения задач
- •Лабораторная работа 6
- •Примеры решения задач
- •Лабораторная работа 7
- •Примеры решения задач
- •Лабораторная работа 9 Обратные операторы Примеры решения задач
- •Литература
- •246019, Г. Гомель, ул. Советская, 104
Лабораторная работа 6
Сжимающие отображения
Примеры решения задач
Задача 1 Является ли отображение F метрического пространства X в себя сжимающим?
Найти х3, где хк+1 = F(хк), х0 = 0. Оценить расстояние от х3 до неподвижной
точки, если F является сжимающим.
Пример 1
![]() .
.
Решение. Оценим расстояние в
![]()
![]()
![]()
![]()
(мы воспользовались неравенством
).
Значит, F является
сжимающим отображением с константой
Липшица
![]() .
.
Построим последовательность
![]() .
По условию
.
По условию
![]() поэтому
поэтому
![]()
![]() .
А так как
.
А так как
![]() ,
,
где
![]() - неподвижная точка, то
- неподвижная точка, то
![]()
Пример 2
![]()
![]()
Решение. Оценим расстояние в

Значит, f – сжимающее
отображение с константой
![]()
По условию,
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
а потому
,
а потому
![]()
(на самом деле, как легко проверить,
![]() является неподвижной точкой).
является неподвижной точкой).
Пример 3
![]() .
.
Решение. Допустим, что отображение F является сжимающим, т.е.
![]() .
.
При y=0 из этого неравенства следует,
что
![]()
![]() .
(1)
.
(1)
Подставив
![]() в левую часть неравенства (1), получим
в левую часть неравенства (1), получим
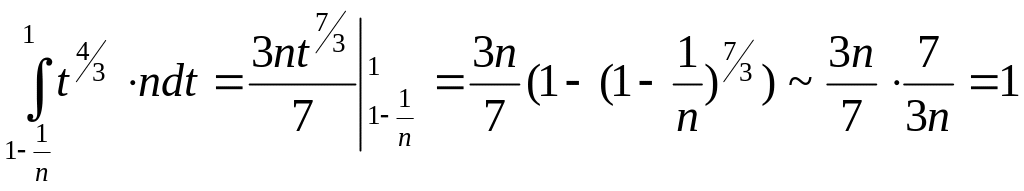 при
при
(мы воспользовались эквивалентностью
![]() при
).
при
).
Правая же часть неравенства (1), как легко
проверить, при этом значении х равна
![]() .
Следовательно, неравенство (1) при
указанных
.
Следовательно, неравенство (1) при
указанных
![]() и
примет вид:
и
примет вид:
![]() противоречие. Значит, F не является
сжимающим. (Аналогичное решение получается
и при
противоречие. Значит, F не является
сжимающим. (Аналогичное решение получается
и при
![]() ).
).
Задача 2 Применим ли принцип сжимающих отображений к заданному интегральному
уравнению в пространстве Х
при
![]() При
При
![]() с точностью до
с точностью до
0,01 найти приближенное решение и сравнить его с точным решением.
![]() (1)
(1)
Решение. Определим отображение
![]() по формуле
по формуле
![]() (2)
(2)
Тогда исходное уравнение запишется в
виде
![]() и искомое решение есть неподвижная
точка отображения
и искомое решение есть неподвижная
точка отображения
![]() .
Метрическое пространство C[0;1]
является полным, поэтому если мы покажем,
что
– сжимающее отображение C[0;1]
в себя, то можно будет применить принцип
сжимающих отображений. То, что отображение
непрерывную на
.
Метрическое пространство C[0;1]
является полным, поэтому если мы покажем,
что
– сжимающее отображение C[0;1]
в себя, то можно будет применить принцип
сжимающих отображений. То, что отображение
непрерывную на
![]() функцию переводит в непрерывную, в
данном случае очевидно (а в общем следует
из свойств интеграла, зависящего от
параметра). Определим, при каких
функцию переводит в непрерывную, в
данном случае очевидно (а в общем следует
из свойств интеграла, зависящего от
параметра). Определим, при каких
![]() отображение
является
сжимающим. Известно, что отображение
отображение
является
сжимающим. Известно, что отображение
![]() (3)
(3)
является сжимающим в C[a;b],
если
![]() где
где
![]() .
При этом константа Липшица
.
При этом константа Липшица
![]() .
(Заметим, что это утверждение дает лишь
достаточное условие сжимаемости). В
данном случае
.
(Заметим, что это утверждение дает лишь
достаточное условие сжимаемости). В
данном случае
![]() ,
,
![]() .
Следовательно,
является сжимающим при
.
Следовательно,
является сжимающим при
![]() т.е., в частности, при
и
т.е., в частности, при
и
![]() .
.
Докажем, что
не является сжимающим при
![]() .
Если допустить, что
– сжимающее, то для
.
Если допустить, что
– сжимающее, то для
![]() и некоторого
и некоторого
![]() должно выполняться неравенство
должно выполняться неравенство
![]() .
.
При
![]() ,
,
![]() последнее неравенство примет вид
последнее неравенство примет вид
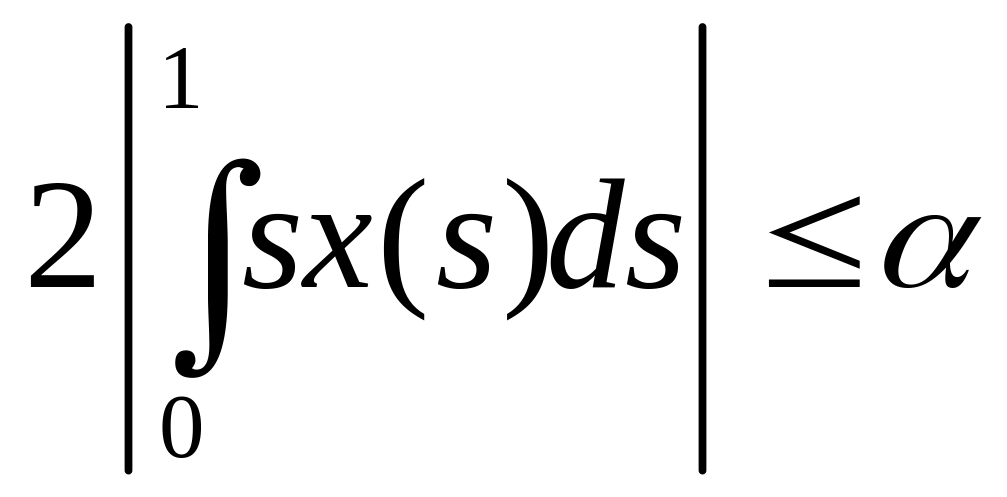 .
А так как
.
А так как
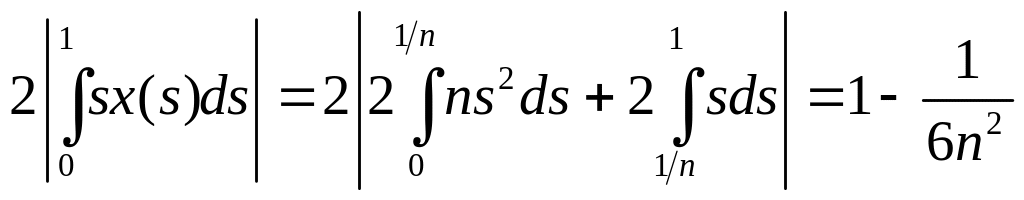 ,
,
То получаем, что
![]() ,
откуда в пределе
,
откуда в пределе
![]() .
Это противоречие доказывает, что
не является сжимающим при
.
Это противоречие доказывает, что
не является сжимающим при
![]() .
.
Решим уравнение (1) при
![]() .
При этом
отображение
- сжимающее, а потому для нахождения
приближённого решения можно воспользоваться
методом итераций (последовательных
приближений). Из уравнения (1) следует,
что его решение имеет вид
.
При этом
отображение
- сжимающее, а потому для нахождения
приближённого решения можно воспользоваться
методом итераций (последовательных
приближений). Из уравнения (1) следует,
что его решение имеет вид
![]() где
где
![]() (4)
(4)
Поскольку
выбирается произвольно, возьмём
![]() .
Дальнейшие приближения находятся по
формулам
.
Дальнейшие приближения находятся по
формулам
![]() ,
,
![]() .
.
Установим номер k, при котором
элемент
![]() будет давать точность приближения 0,01.
Используем оценку погрешности (х -
точное решение)
будет давать точность приближения 0,01.
Используем оценку погрешности (х -
точное решение)
![]() .
.
В нашем случае
![]() .
Тогда
.
Тогда
![]() .
.
![]() .
.
Следовательно,
![]() ,
,
А потому искомое k
определяется из неравенства:
![]() .
Поскольку k=3 ему удовлетворяет,
.
Поскольку k=3 ему удовлетворяет,
![]() будет приближенным решением исходного
уравнения с точностью 0,01. Найдём
:
будет приближенным решением исходного
уравнения с точностью 0,01. Найдём
:
![]() ,
,
![]() .
.
Итак, приближённое решение с нужной
точностью есть
![]()
Точное решение имеет вид
![]() (см. формулу (4)). Подставив
(см. формулу (4)). Подставив
![]() в (1), получим:
в (1), получим:
![]() .
Отсюда
.
Отсюда
![]() ,
,
![]()
![]() .
Следовательно, точное решение есть
.
Следовательно, точное решение есть
![]()
Сравним его с приближённым:
![]() .
.
Замечание. Первую часть решения можно сократить, если воспользоваться тем фактом, что норма линейного оператора
![]()
в пространстве C[0;1] дается формулой
![]() .
.
Поскольку норма есть точная константа
в неравенстве ограниченности, отображение
А1 является сжимающим
тогда и только тогда, когда
![]() То же верно и для отображения
То же верно и для отображения
![]() (почему?).
(почему?).
Задания лабораторной работы
Задача 1 Является ли отображение F метрического пространства X в себя сжимающим?
Найти х3, где хк+1 = F(хк), х0 = 0. Оценить расстояние от х3 до неподвижной
точки, если F является сжимающим.
№ |
X |
F |
1.1 |
|
|
1.2 |
|
|
1.3 |
C[-1;1] |
|
1.4 |
|
|
1.5 |
C[-1;1] |
|
1.6 |
|
|
Задача 2 Применим ли принцип сжимающих отображений к заданному интегральному
уравнению в пространстве Х
при
![]() ?
При
с точностью
?
При
с точностью
до 0,01 найти приближённое решение и сравнить его с точным решением.
№ |
Х |
|
|
|
Уравнение |
2.1 |
C[0;1] |
|
|
|
|
2.2 |
C[-1;1] |
|
|
|
|
2.3 |
C[-2;2] |
|
|
|
|
2.4 |
C[-1;1] |
|
|
|
|
2.5 |
C[0;1] |
|
|
|
|
2.6 |
C[-1;1] |
|
|
|
|
