
- •Оглавление
- •Введение
- •1. Теория функций комплексного переменного
- •Комплексные числа и операции над ними
- •1.1.1. Определение комплексного числа
- •1.1.2. Формы записи комплексных чисел
- •1.1.3. Формула Муавра и извлечение корня n-ой степени из комплексного числа
- •1.2. Функции комплексного переменного
- •1.3. Дифференцирование функций комплексного переменного
- •1.3.1. Определение производной
- •1.3.2. Необходимые и достаточные условия дифференцируемости функции комплексного переменного
- •1.3.3. Производные основных элементарных функций
- •1.3.4. Восстановление аналитической функции по известной действительной или мнимой части
- •Интегрирование функций комплексного переменного
- •1.4.1. Определение интеграла от функции комплексного переменного
- •1.4.2. Теорема Коши. Вычисление интегралов от аналитических функций
- •2. Теория рядов
- •2.1. Числовые ряды
- •2.1.1.Основные понятия Пусть дана последовательность чисел (вещественных или комплексных)
- •Свойства сходящихся рядов
- •Замечание. Условие является необходимым, но не достаточным для сходимости, т.Е. Если , то ряд может сходиться, а может и расходиться.
- •Т. Е. Сходимость ряда равносильна тому, что сумма любого числа членов ряда, следующих за достаточно большим номером, должна быть произвольно мала.
- •2.1.2. Достаточные признаки сходимости положительных рядов
- •Пусть даны два положительных ряда и .
- •2.1.3. Сходимость рядов с произвольными членами
- •2.2. Функциональные ряды
- •2.2.1. Сходимость функционального ряда
- •Функциональные свойства суммы сходящегося ряда
- •2.2.2. Степенные ряды
- •Область сходимости степенных рядов
- •Ряды Тейлора и Маклорена
- •2.3. Ряды Фурье
- •2.3.1. Тригонометрический ряд Фурье. Периодические функции.
- •2.3.2. Сходимость ряда Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода 2l
- •2.3.3. Интеграл Фурье
- •3. Теория вероятностей
- •Случайные события и их вероятности
- •Классификация событий
- •3.1.2. Операции над событиями
- •3.1.3. Аксиоматическое определение вероятности
- •Примеры вероятностных пространств
- •Конечное вероятностное пространство
- •2. Непрерывное вероятностное пространство
- •3.1.4. Условная вероятность. Теорема умножения вероятностей.
- •3.1.5. Формула полной вероятности. Формула Байеса
- •3.1.6. Последовательность независимых испытаний. Формула Бернулли
- •3.1.7. Статистическое определение вероятности
- •3.2. Случайные величины, их распределения и числовые
- •3.2.1.Дискретные случайные величины
- •3.2.2. Функция распределения. Плотность распределения
- •3.2.3. Математическое ожидание случайной величины
- •3.2.4. Дисперсия случайной величины
- •3.2.5. Примеры законов распределения случайных величин Дискретные случайные величины
- •1. Биномиальное распределение
- •2. Распределение Пуассона
- •3. Геометрическое распределение
- •4. Гипергеометрическое распределение
- •Непрерывные случайные величины
- •5. Равномерное распределение
- •6. Показательное распределение
- •7. Нормальное распределение
- •3.3. Системы случайных величин
- •3.3.1. Закон распределения системы случайных величин
- •Условный закон распределения
- •3.3.2. Числовые характеристики случайного вектора
- •3.3.3. Предельные теоремы теории вероятностей
- •4. Математическая статистика
- •4.1. Методы статистического описания результатов наблюдений
- •4.1.1. Статистическое распределение выборки
- •4.1.2. Эмпирическая функция распределения
- •4.2. Оценки параметров распределения
- •4.2.1.Точечные оценки параметров распределения
- •4.2.2. Интервальные оценки параметров распределения
- •4.3. Проверка статистических гипотез
- •4.4. Статистические оценки параметров линейной корреляционной зависимости (между двумя случайными величинами)
- •5. Контрольная работа № 7. Задания
- •5.1. Пример выполнения контрольной работы № 1. Вариант 0.
- •5.2. Варианты заданий контрольной работы № 7
- •6. Контрольная работа № 8. Задания
- •6.1. Пример выполнения контрольной работы № 2. Вариант № 0.
- •6.2. Варианты заданий контрольной работы № 8
2. Теория рядов
2.1. Числовые ряды
2.1.1.Основные понятия Пусть дана последовательность чисел (вещественных или комплексных)
Определение.
Выражение
![]() называют числовым
рядом, или
просто рядом,
а сами числа
называют числовым
рядом, или
просто рядом,
а сами числа
![]() -
членами ряда.
-
членами ряда.
Числовой
ряд будем обозначать
![]() .
.
Ряд
считается заданным, если известен общий
член ряда
,
выраженный как функция его номера n:
![]() .
.
Определение.
Сумма первых n
членов ряда
![]() называется
n-й
частичной суммой ряда
и обозначается
называется
n-й
частичной суммой ряда
и обозначается
![]() ,
т.е.
,
т.е.
![]()
Рассмотрим частичные суммы:
![]() ,…,
,…,![]()
Определение.
Если последовательность
![]() имеет конечный предел:
имеет конечный предел:
![]() ,
то говорят, что ряд
сходится.
В этом случае, предел
,
то говорят, что ряд
сходится.
В этом случае, предел
![]() называют суммой
ряда и пишут:
называют суммой
ряда и пишут:
![]() .
.
Ряд
расходится,
если
последовательность
![]() не
имеет предела или он равен
не
имеет предела или он равен
![]() .
Если
.
Если
![]() ,
то говорят, что сумма ряда равна
,
и пишут:
,
то говорят, что сумма ряда равна
,
и пишут:
![]() .
.
Пример.
Показать,
что числовой ряд
![]() расходится.
расходится.
Решение.
Запишем n-ю
частичную сумму ряда. Имеем
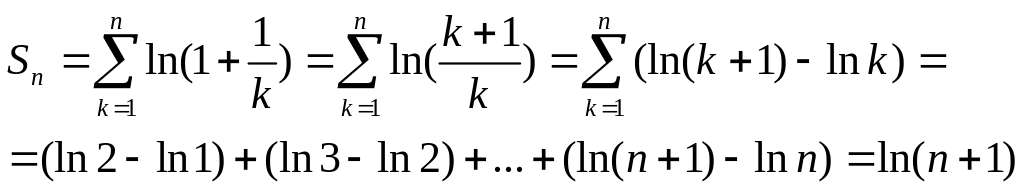
Тогда
при
![]() имеем
имеем
![]() .
Следовательно, ряд расходится, и
считается,что его сумма равна
.
.
Следовательно, ряд расходится, и
считается,что его сумма равна
.
Пример.
Показать, что ряд
![]() сходится.
сходится.
Решение.
Частичные суммы ряда имеют вид:
![]() ,
,
![]() ,
…,
,
…,
![]() .
Вычислим сумму ряда:
.
Вычислим сумму ряда:
![]() ,
т.е. ряд сходится, и его сумма равна 1.
,
т.е. ряд сходится, и его сумма равна 1.
Пример.
Исследовать
на сходимость ряд, члены которого
образуют геометрическую прогрессию:
![]() =
=
![]()
![]() .
.
Решение.
Сумма первых
n
членов прогрессии вычисляется по формуле
![]() .
Найдем предел этой суммы:
.
Найдем предел этой суммы:
![]() .
.
В зависимости от величины q имеем:
если
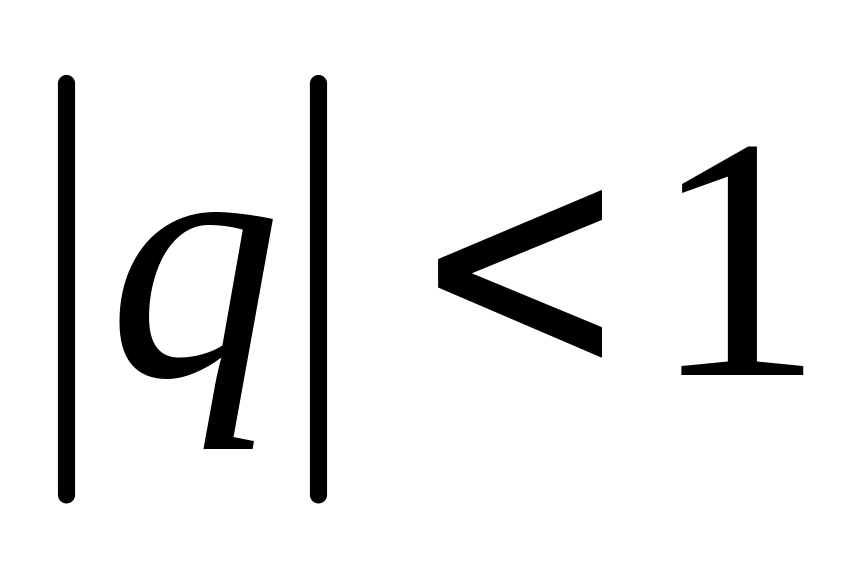 ,
то
,
то
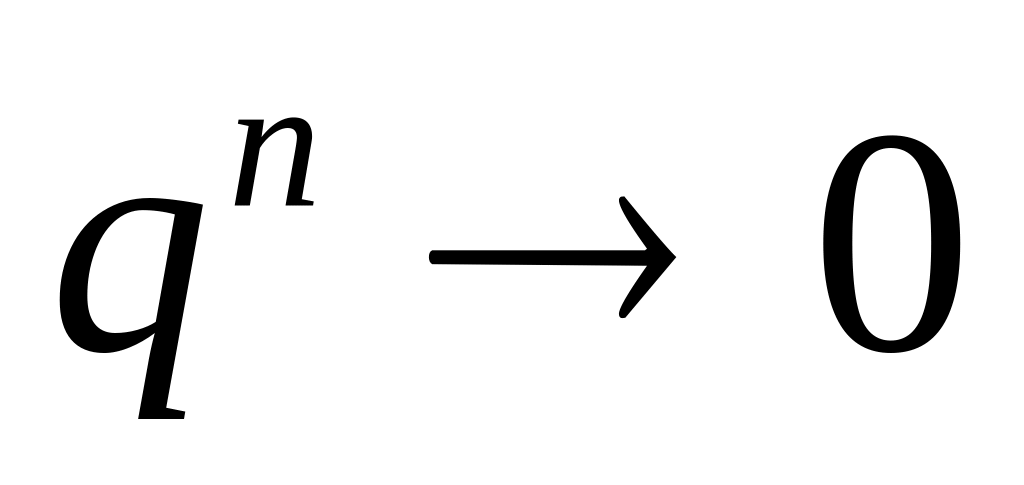 при
.
Поэтому
при
.
Поэтому
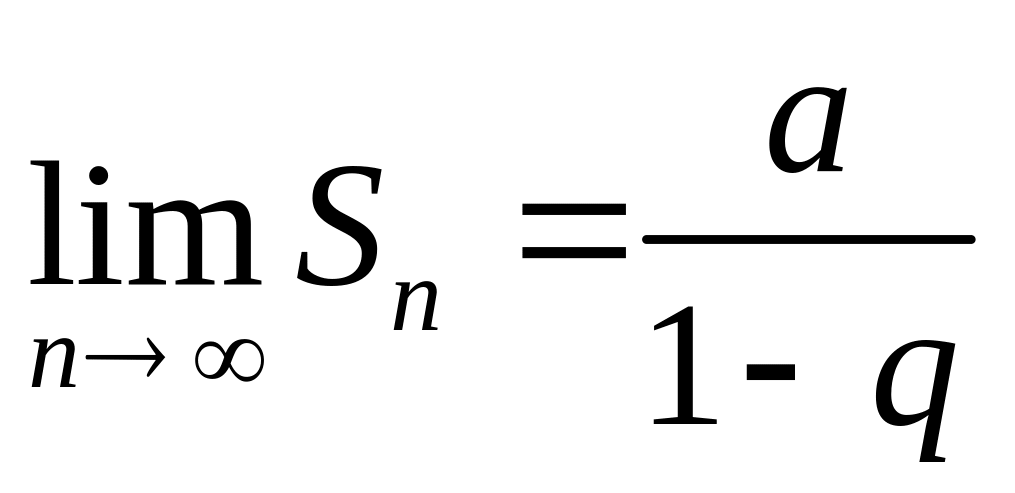 ,
ряд сходится, его сумма равна
,
ряд сходится, его сумма равна
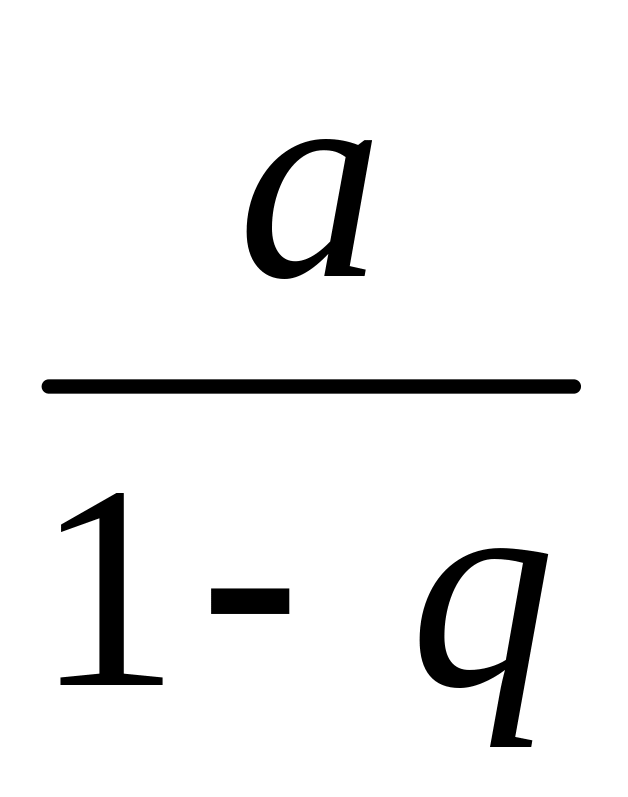 ;
;если
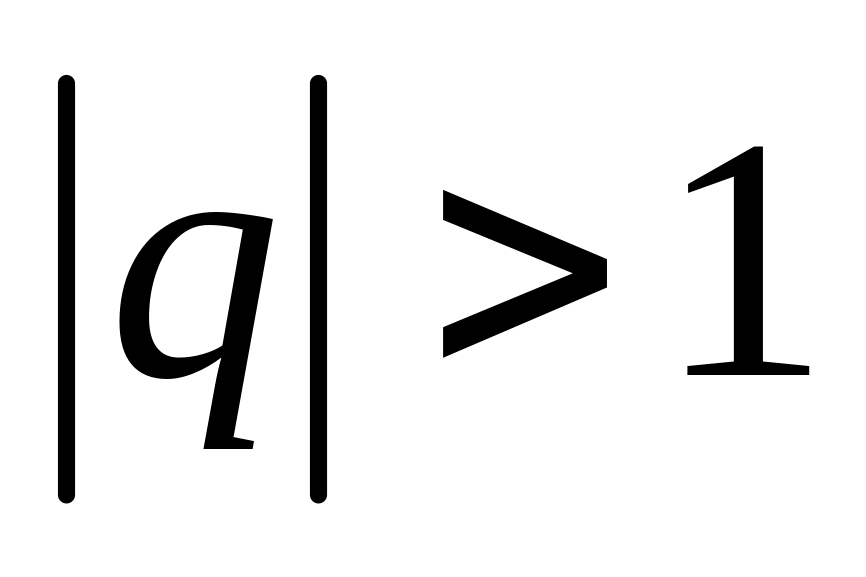 ,
то
,
то
 при
.
Поэтому
при
.
Поэтому
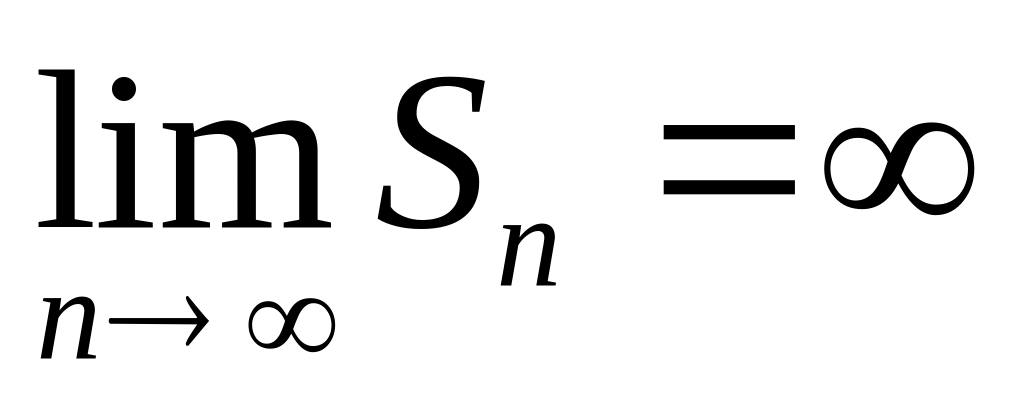 ,
ряд расходится;
,
ряд расходится;если
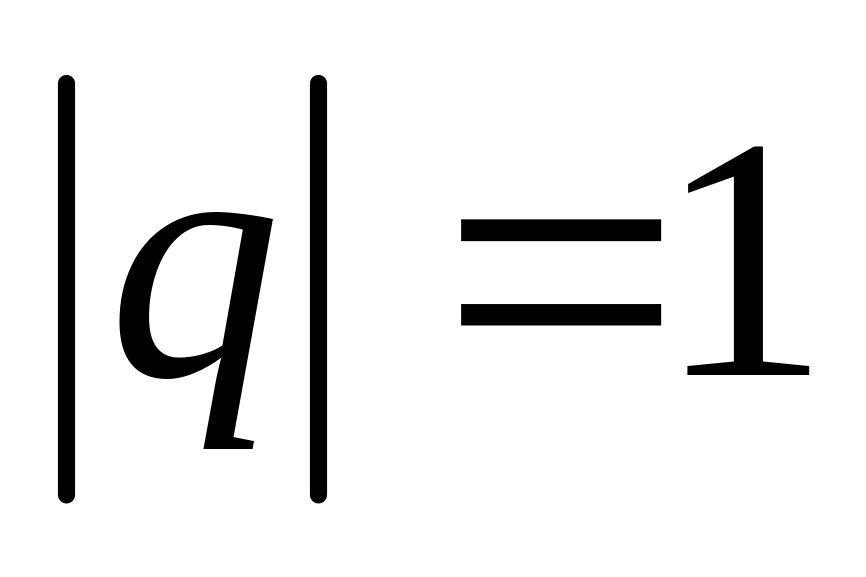 ,
то при
,
то при
 ряд принимает вид
ряд принимает вид
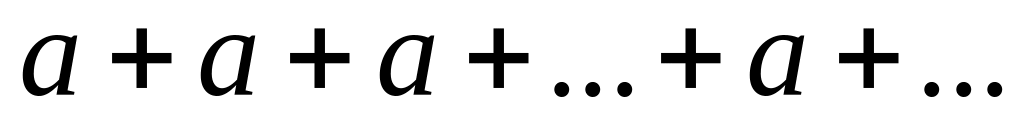 ,
,
для
него
![]() и
,
т.е. он расходится;
и
,
т.е. он расходится;
при
![]() ряд принимает вид
ряд принимает вид
![]() , в этом случае
, в этом случае
![]() при четном n
и
при четном n
и
![]() при нечетном n.
Следовательно,
при нечетном n.
Следовательно,
![]() не существует, ряд расходится.
не существует, ряд расходится.
Таким
образом, ряд сходится при
и расходится при
![]() .
Такой ряд будем называть рядом
геометрической прогрессии.
.
Такой ряд будем называть рядом
геометрической прогрессии.
Свойства сходящихся рядов
Теорема 1. Если в ряде отбросить конечное число первых членов, то полученный ряд и ряд сходятся или расходятся одновременно.
Теорема
2. Если ряды
и
![]() сходятся
и С
– некоторое число, то ряды
сходятся
и С
– некоторое число, то ряды
![]() и
и
![]() также
сходятся, при этом
также
сходятся, при этом
![]() ,
,
![]() .
.
Теорема
3. (необходимый признак сходимости ряда).
Если ряд
сходится,
то
![]() .
.
Следствие
(достаточное условие расходимости
ряда). Если
![]() или
или
![]() не существует, то ряд
расходится.
не существует, то ряд
расходится.
Замечание. Условие является необходимым, но не достаточным для сходимости, т.Е. Если , то ряд может сходиться, а может и расходиться.
Пример.
Исследовать
сходимость ряда
![]() .
.
Решение.
Ряд
расходится, т.к.
![]() ,
т.е. выполняется достаточное условие
расходимости ряда.
,
т.е. выполняется достаточное условие
расходимости ряда.
Пример.
Исследовать
сходимость ряда
![]()
Решение.
Данный ряд
расходится, т.к.
![]() .
.
Пример.
Исследовать
сходимость ряда
![]() .
.
Решение.
=![]() ,
для него
,
для него
![]() ,
но этот ряд является расходящимся.
Докажем это. Предположим, что ряд сходится
и его сумма равна S,
тогда имеем
,
но этот ряд является расходящимся.
Докажем это. Предположим, что ряд сходится
и его сумма равна S,
тогда имеем
![]() .
С другой стороны,
.
С другой стороны,
![]() .
Значит,
.
Значит,
![]() .
Полученное противоречие, доказывает,
что данный ряд не может сходиться. Данный
ряд называется гармоническим.
.
Полученное противоречие, доказывает,
что данный ряд не может сходиться. Данный
ряд называется гармоническим.
Теорема
4 (Критерий
Коши).
Для того, чтобы ряд
сходился, необходимо и достаточно, чтобы
для
![]()
![]() такой, что при
такой, что при
![]() неравенство
неравенство
![]() выполнялось для любого конечного
выполнялось для любого конечного
![]() .
.
