4.2. Оценки параметров распределения

4.2.1.Точечные оценки параметров распределения

Зная эмпирическую функцию распределения, мы можем оценить характер теоретической функции распределения генеральной совокупности. Однако как в теории, так и на практике бывает важно оценить отдельные свойства случайной величины на основе экспериментальных данных.

Распределение случайной величины Х характеризуется целым рядом параметров или числовых характеристик, например: математическое ожидание, дисперсия, мода и так далее. Используя выборку исследуемой случайной величины, можно вычислить приближенные значения каждого из неизвестных параметров, называемые в статистике точечными оценками параметров (т.е. оценивание параметра осуществляется одним числом, точкой на числовой оси).

Точечные оценки параметров распределения являются значениями некоторых функций элементов выборки, которые называются статистиками. Например, для оценки математического ожидания случайной величины Х используют статистику 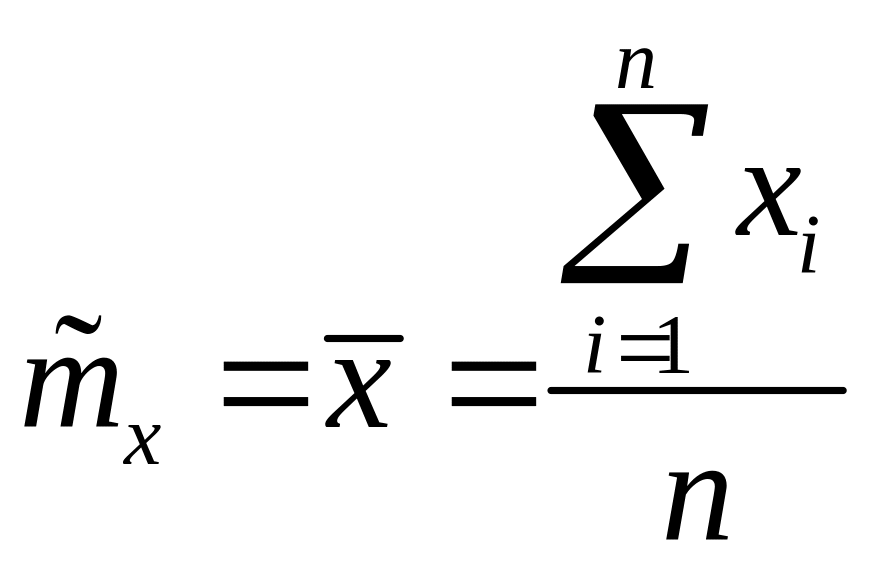, которая называется выборочное среднее.

Оценку параметра будем обозначать символом с тильдой: .

Очевидно, что значения статистик изменяются от выборки к выборке случайным образом, т.е. статистики являются случайными величинами. Для оценки данного параметра можно использовать несколько разных статистик, получая при этом различные значения оценок. Очевидно, что для наилучшей оценки следует взять такую статистику, значения которой для различных выборок из данной генеральной совокупности были бы «в среднем» близки к истинному значению параметра, который оценивается.

Качество оценок характеризуют следующими свойствами.

• Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру: .

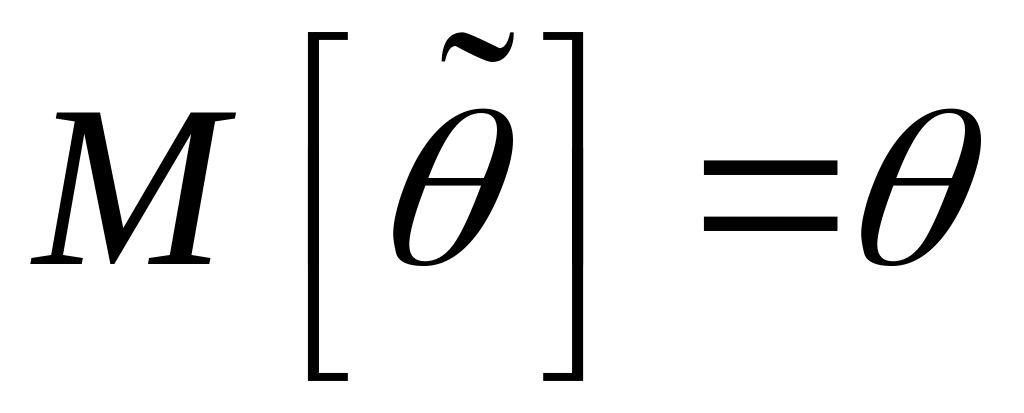• Оценка 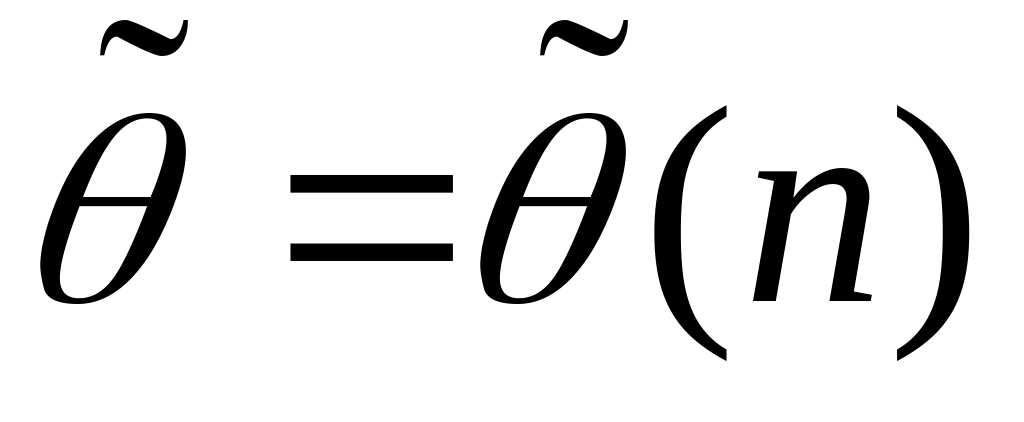называется состоятельной, если при увеличении объема выборки оценка сходится по вероятности к . Это означает, что для любых 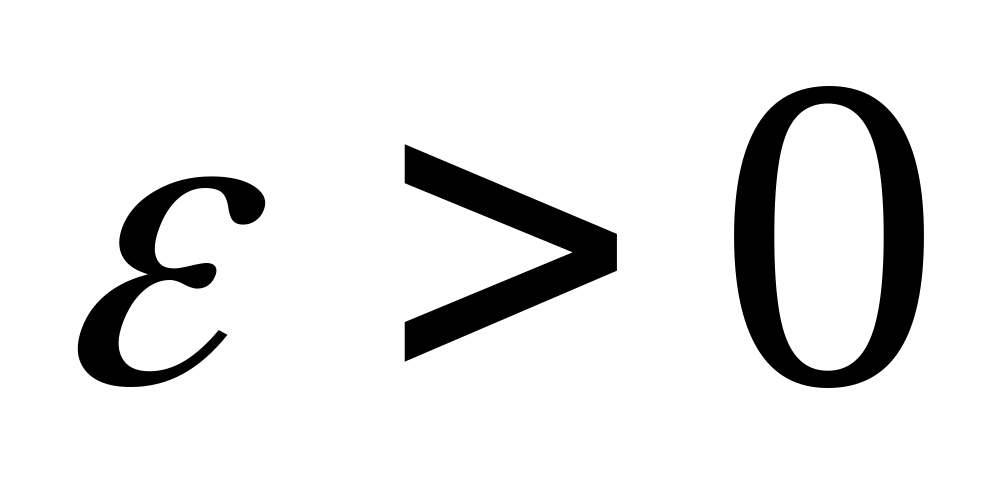и 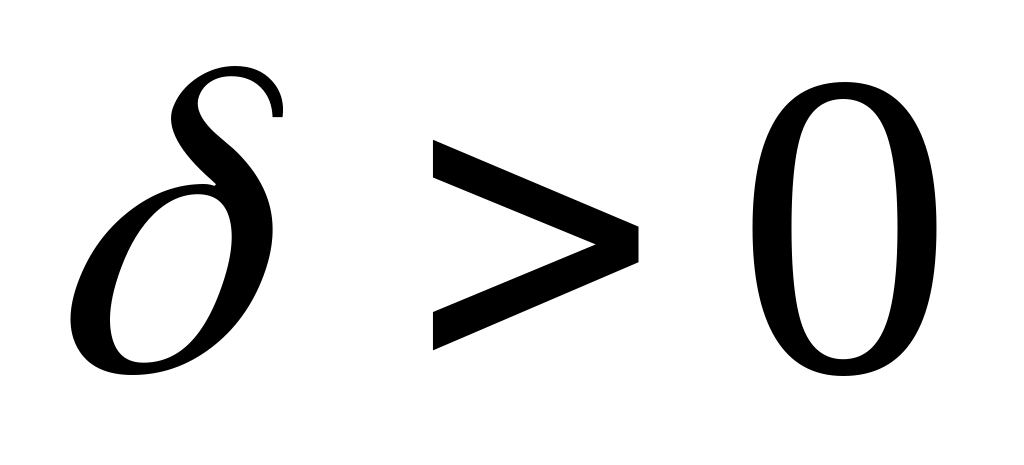существует 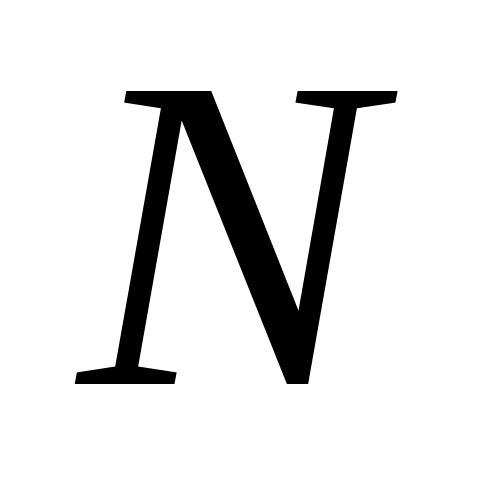такое, что при выполняется неравенство: 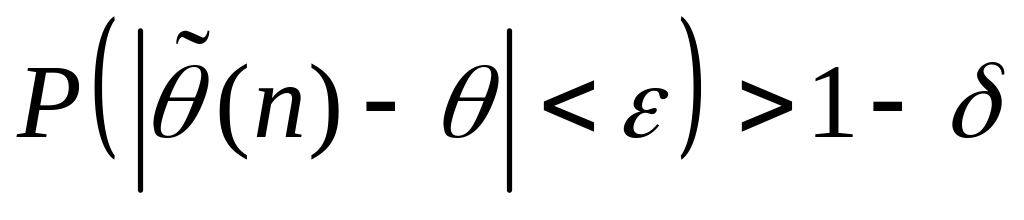(вероятность того, что оценка отличается от истинного значения не больше, чем на , близка к единице).

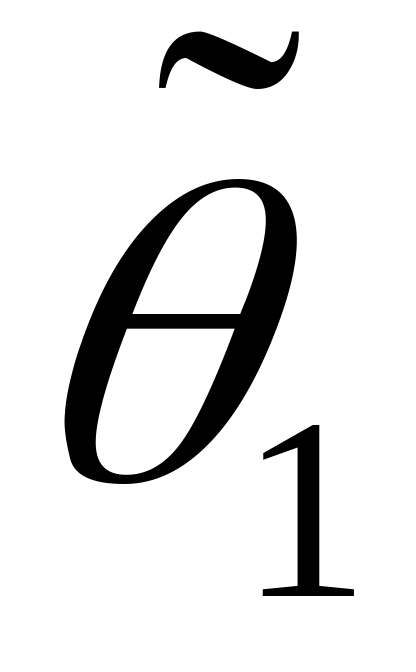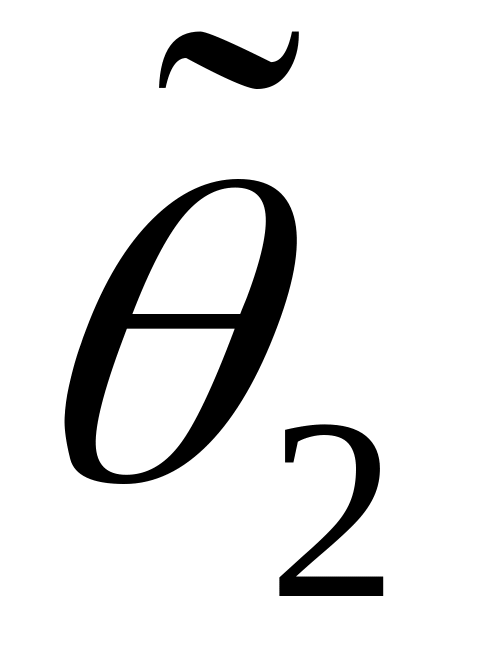• Пусть и - две различные несмещенные оценки параметра . Если 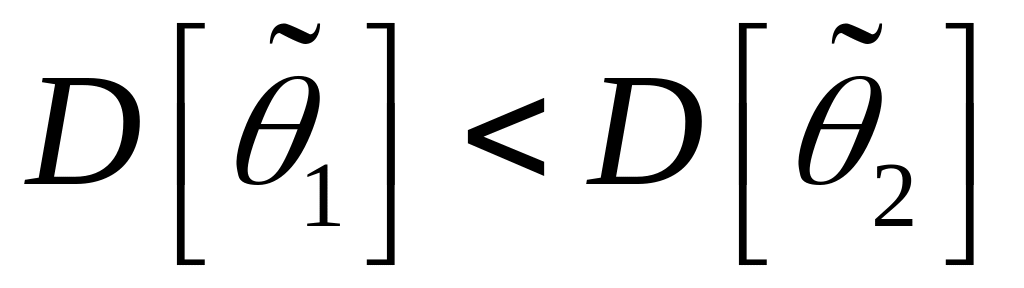, то говорят, что оценка , более эффективна, чем оценка .

• Пример. Несмещенной и состоятельной оценкой математического ожидания случайной величины Х будет выборочное среднее: ,

а несмещенной и состоятельной оценкой дисперсии будет исправленная выборочная дисперсия: .

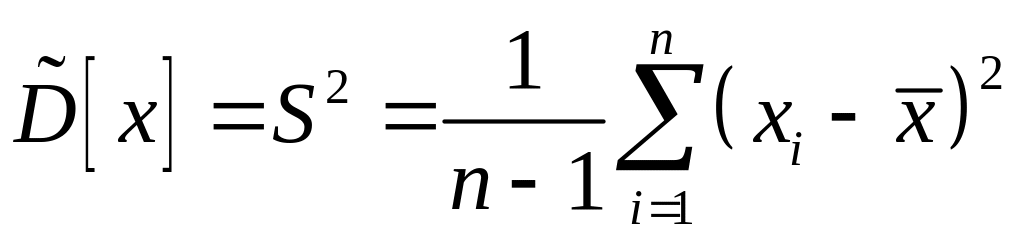Метод максимального правдоподобия

Для нахождения точечных оценок параметров распределения можно использовать метод максимального правдоподобия. Этот метод основан на следующем интуитивном представлении: в большинстве случаев в эксперименте наблюдается именно то значение случайной величины Х, при котором плотность вероятности близка к максимальному значению.

Согласно методу максимального правдоподобия для нахождения оценки параметра на основании выборки :

1. составляют функцию правдоподобия:

,

(это функция аргумента и элементов выборки, - плотность распределения случайной величины Х, содержащая неизвестный параметр, - значение плотности при );

2) находят то значение , при котором функция правдоподобия принимает максимальное значение: . Для этого находят точку максимума функции :

.

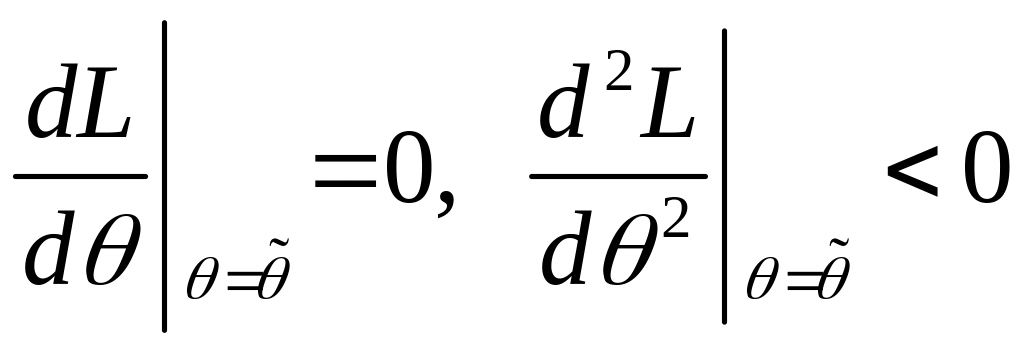Иногда для упрощения вычислений удобно рассматривать логарифм функции правдоподобия.

3) в качестве точечной оценки параметра принимают найденное значение .

Определение. Оценку называют оценкой наибольшего (максимального) правдоподобия.

Оценки параметров, полученные по методу максимального правдоподобия, асимптотически нормально распределены и для некоторых законов распределения генеральной совокупности имеют минимальную дисперсию.

Пример. Найти оценку параметра показательного распределения , если в результате испытаний величины Х, распределенной по показательному закону, получены значения .

Решение. Составим функцию правдоподобия:

.

Для упрощения вычислений найдем: 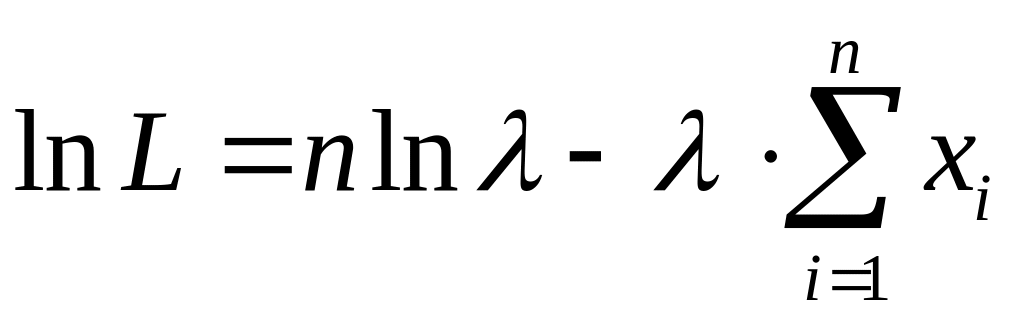, и его точку максимума:

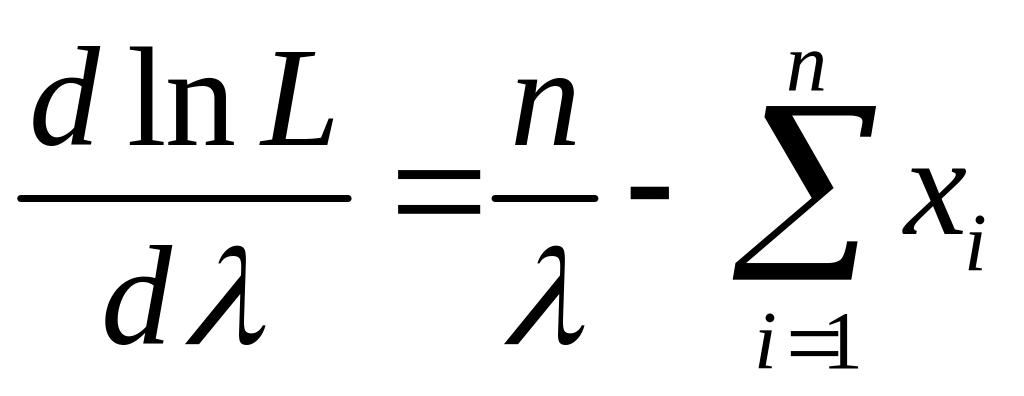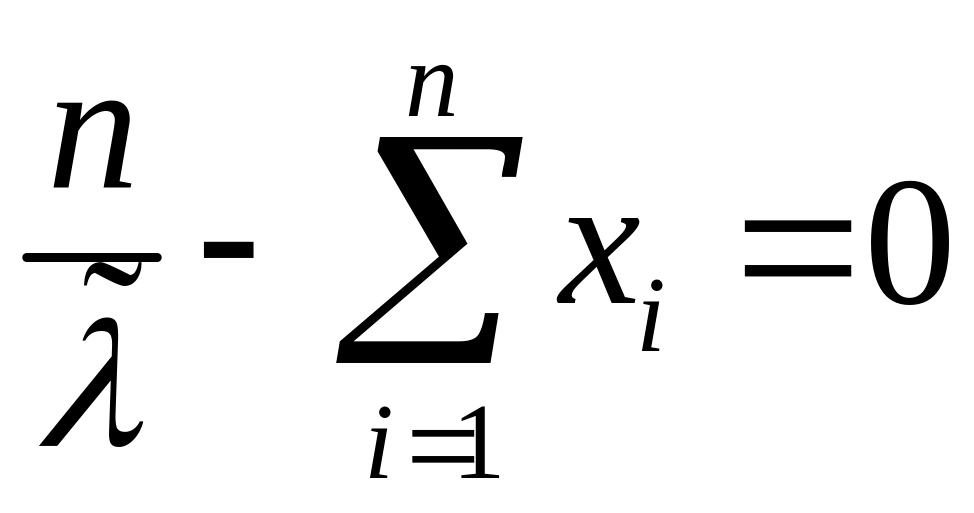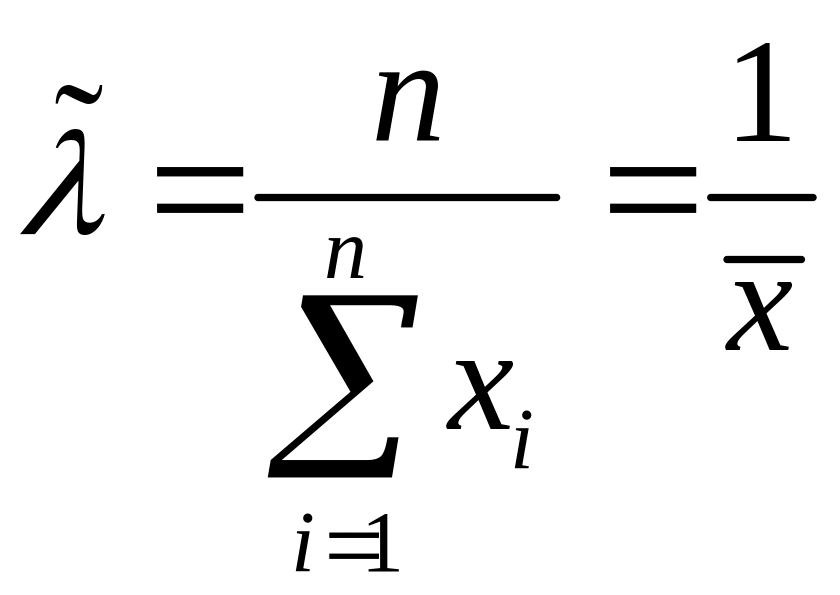, , (здесь - выброчное среднее).

Так как 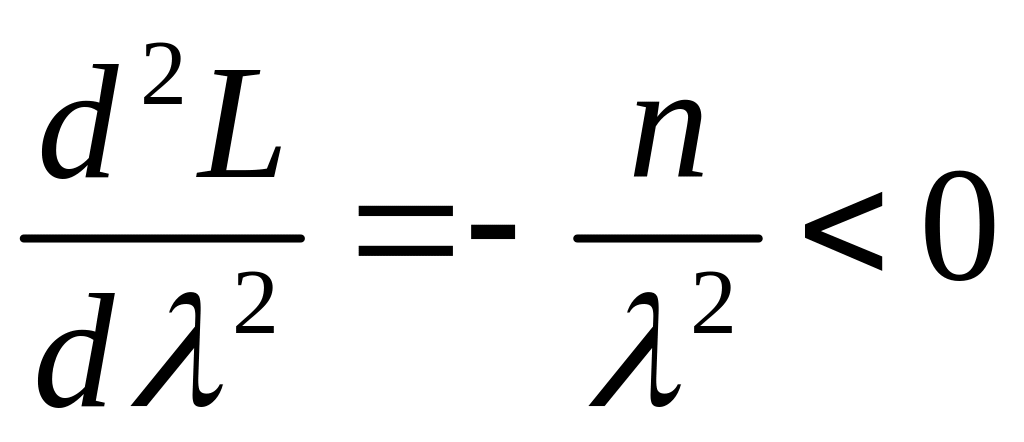, то функция правдоподобия принимает максимальное значение при , значит - искомая оценка параметра .