Интегрирование функций комплексного переменного
1.4.1. Определение интеграла от функции комплексного переменного
Пусть
на комплексной плоскости задана
ориентированная кусочно-гладкая кривая
,
вдоль которой определена функция
.
Замечание. Дуга называется гладкой, если она может быть задана непрерывно-дифференцируемой функцией. Кривая, состоящая из конечного числа гладких дуг, называется кусочно – гладкой.
Разобьем
эту кривую на
частей
точками
,
пронумерованными в направлении от
- начальной точки кривой
,
до
- конечной точки
.
Обозначим через
(
).
В каждой части выберем произвольно
точку
(
)
и составим сумму:
,
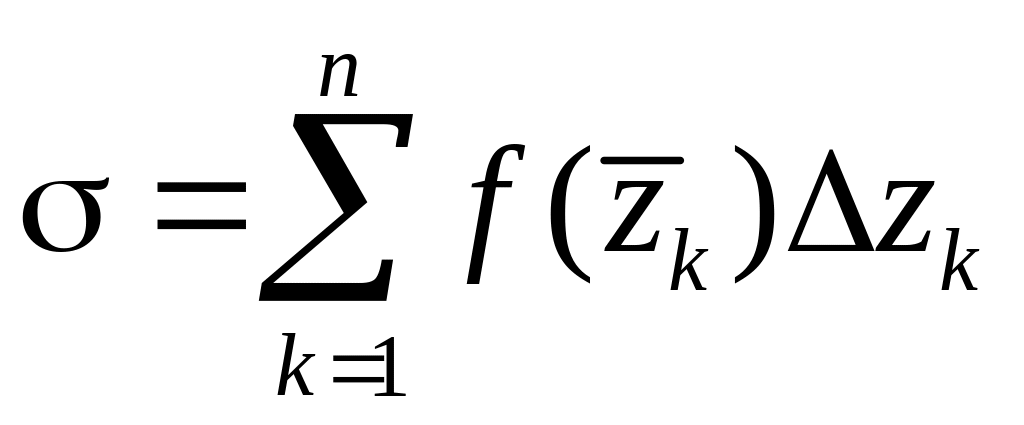которую назовем интегральной суммой.
Устремим
в бесконечность так, чтобы
.
Определение.
Если существует предел интегральной
суммы
при условии произвольного способа
разбиения кривой
на части, произвольного выбора точек
(
)
и при условии
,
то этот предел называется интегралом
от функции
по дуге (контуру)
и обозначается:
.
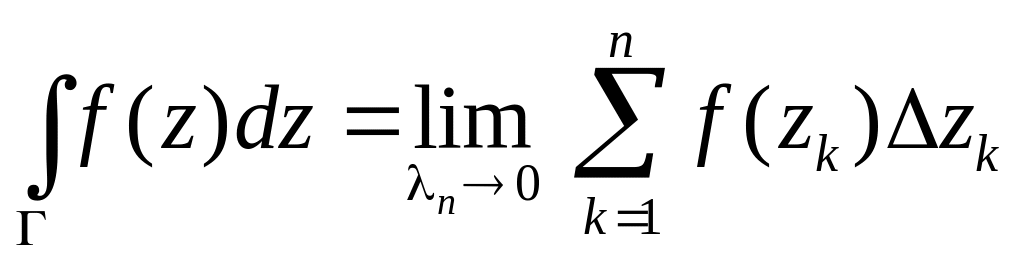Из
определения интеграла следует, что его
значения зависят не только от функции
,
но и от пути интегрирования Г. Если
кривая
замкнутая (точки
и
совпадают), то интеграл обозначают
символом:
.
Если
функция
непрерывна вдоль кривой
,
то интеграл
существует.
Пусть и ,
тогда
.
Таким образом, интеграл от функции комплексного переменного равен сумме двух криволинейных интегралов 2-го рода от вещественных функций:
.
Если кривая задана параметрическим уравнением:
(или
),
тогда:
.
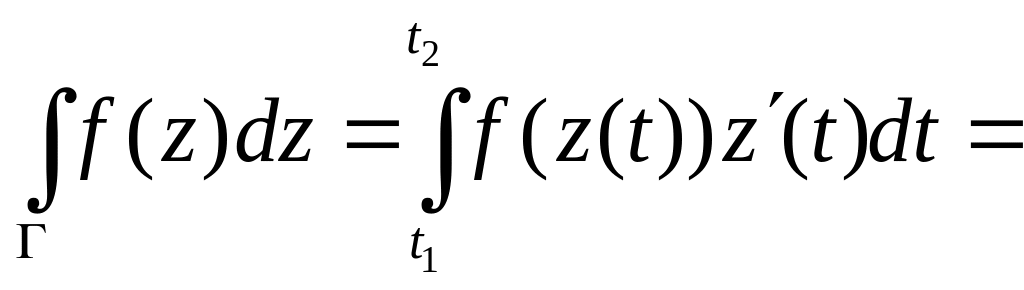
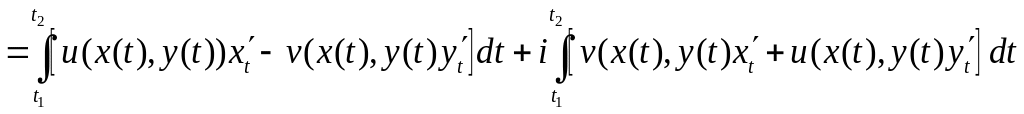Замечание.
Довольно
часто в качестве параметра
выбирают угол:
.
Поскольку интеграл от функции комплексного переменного сводится к криволинейным интегралам второго рода от действительных функций, то его свойства будут аналогичны известным свойствам криволинейных интегралов:
,
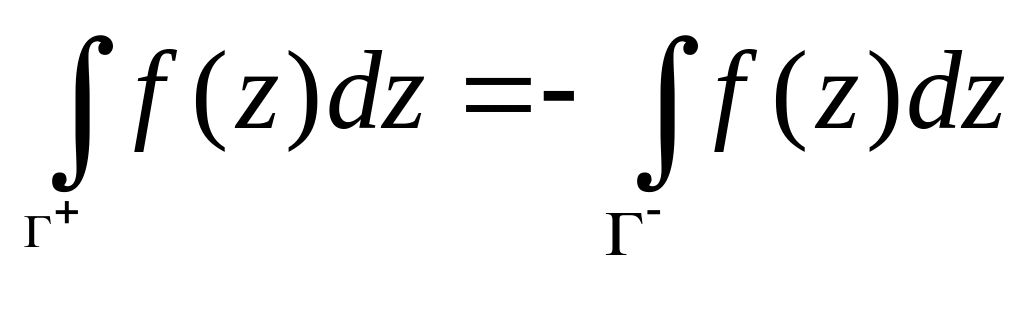где
и
- один и тот же контур, проходимый в
положительном и отрицательном направлениях
(в качестве положительного направления
обхода замкнутого контура принимается
направление, при котором внутренняя
область, ограниченная данным замкнутым
контуром, остается слева от направления
движения).
.
.
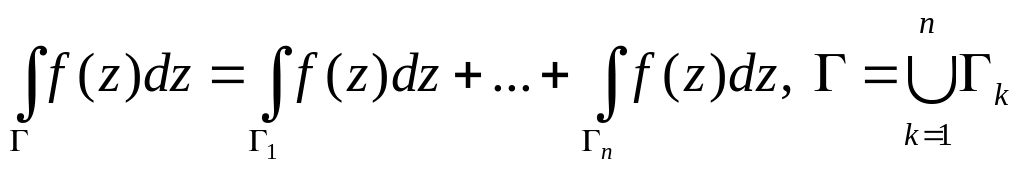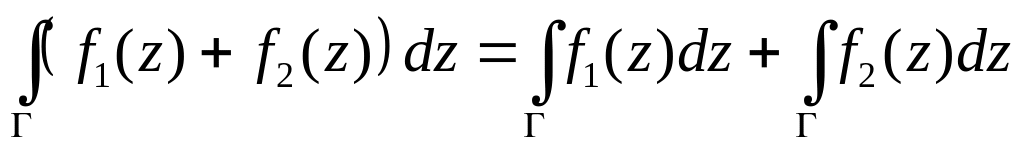.Если вдоль кривой :
,
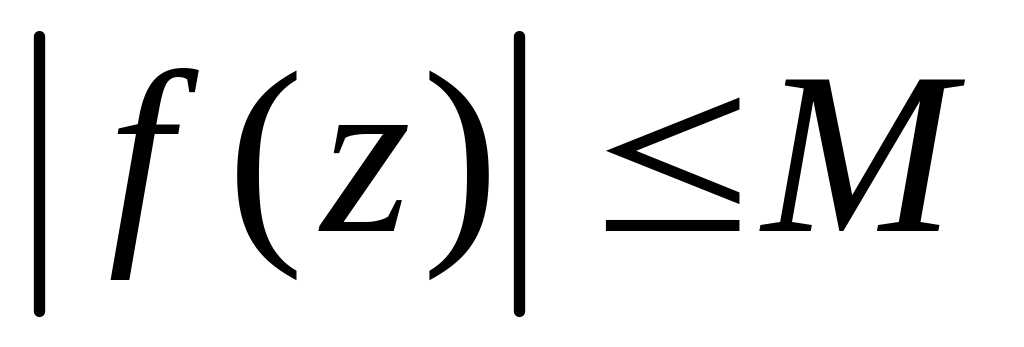и длина кривой
есть
,
то
.
,
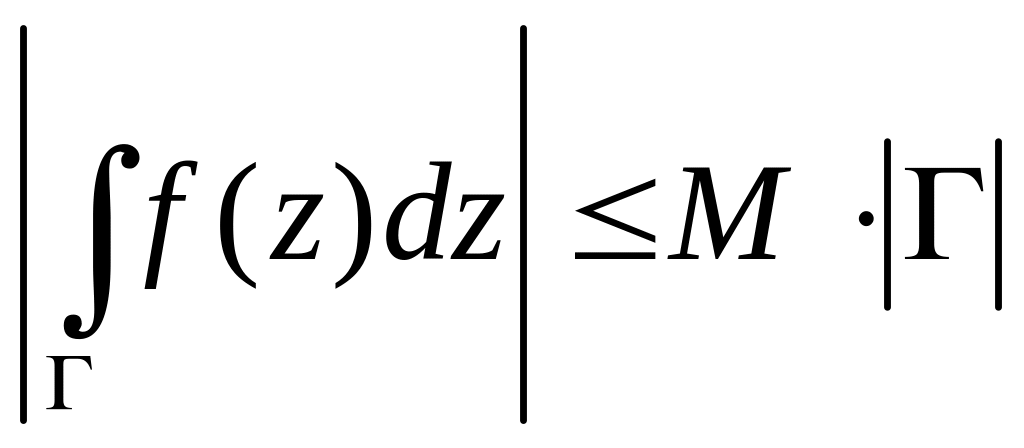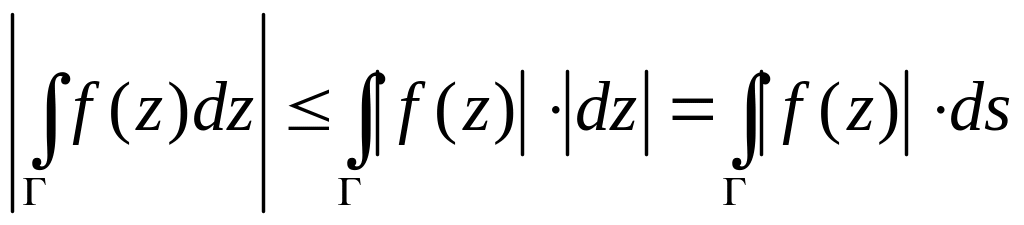- дифференциал длины дуги.
Пример.
Вычислить интеграл
,
где
- дуга параболы
от точки 0 до точки
.
Решение.
Так как для всех точек кривой
имеем:
,
то
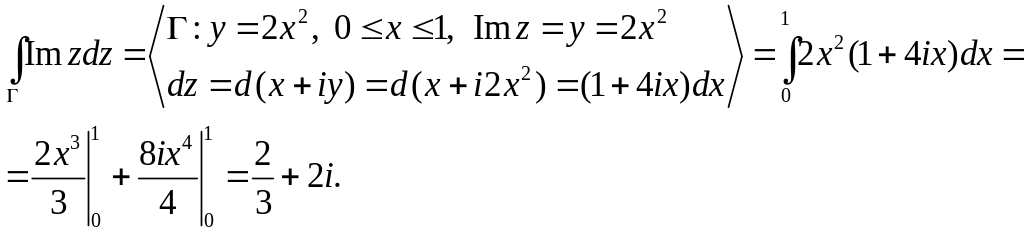
Пример.
Вычислить интеграл
,
где
- часть окружности
,
.
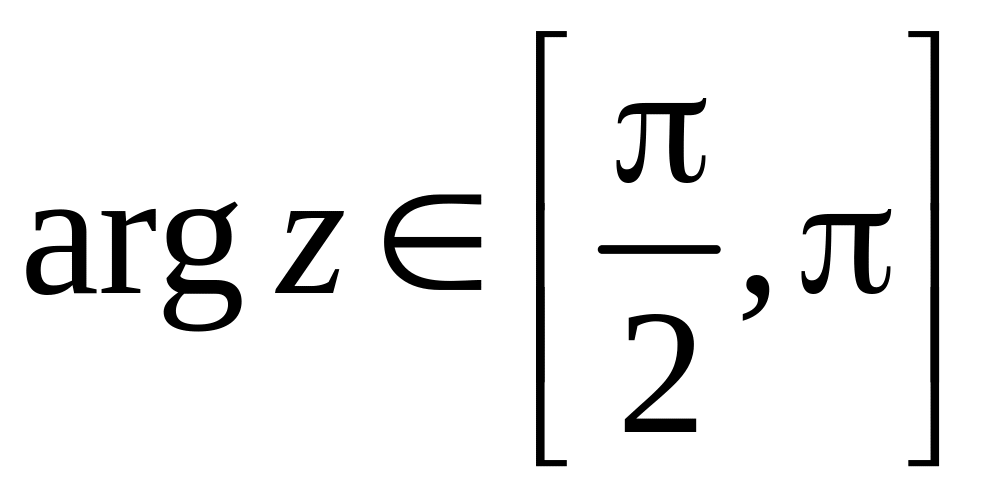Решение.
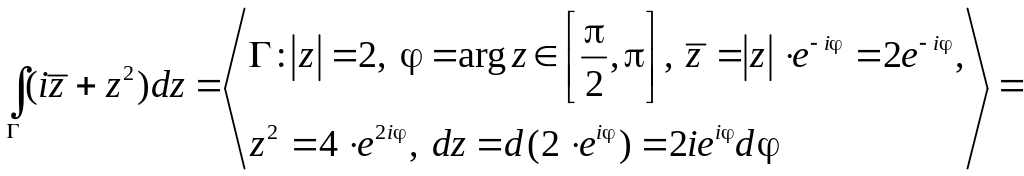
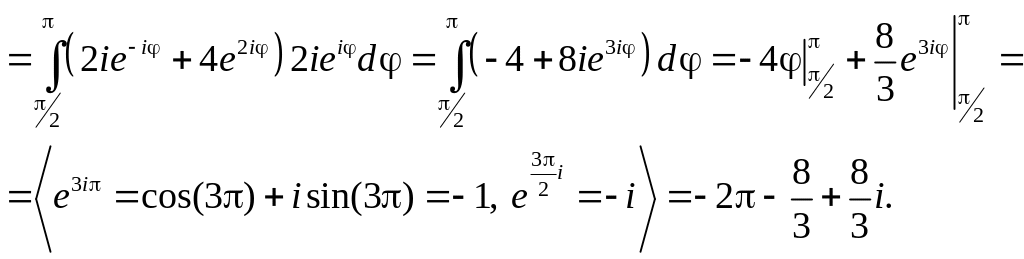
1.4.2. Теорема Коши. Вычисление интегралов от аналитических функций
Мы уже отмечали, что условия, при выполнении которых функция является аналитической, достаточно жесткие. Это и обуславливает справедливость следующей теоремы.
Теорема
2 (Теорема Коши). Если
- односвязная область комплексной
плоскости и
- однозначная аналитическая в этой
области функция, то для любой замкнутой
спрямляемой кривой
,
лежащей в области
,
интеграл от
вдоль
равен нулю:
.
Отметим, что теорема Коши остается справедливой и для многосвязной области.
Из
теоремы 2 вытекает, что интегралы от
аналитической функции вдоль любых двух
кривых
и
с общим началом
и концом
имеют равные значения.
В
самом деле, кривая
является замкнутой, и, следовательно,
откуда
Это
означает, что
интеграл от
функции
,
аналитической
в односвязной области
,
не зависит от кривой
(от
пути интегрирования), а зависит только
от начальной и конечной точек этой
кривой. Поэтому для интеграла вдоль
произвольной спрямляемой кривой
,
соединяющей точки
и
,
можно пользоваться обозначением
.
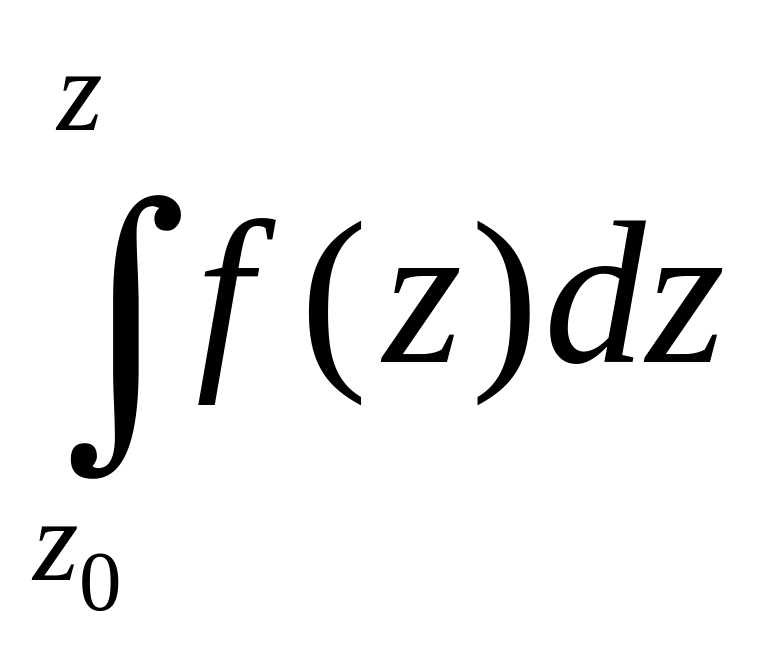Рассмотрим интеграл от аналитической функции, если конечная точка – переменная, т.е. есть некоторая функция от верхнего предела:
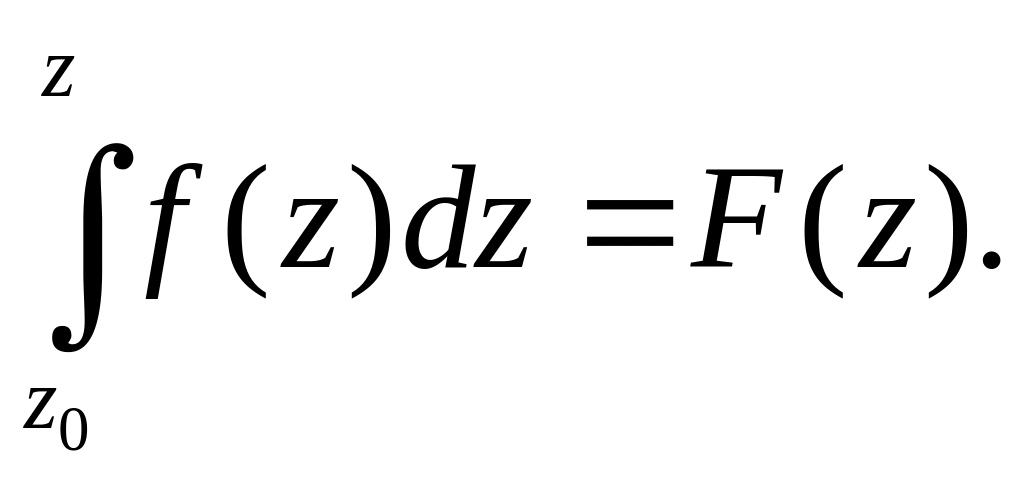
Можно
показать, что
- аналитическая функция, и что ее
производная равна
.
Таким образом, интеграл
является первообразной
для подынтегральной функции (определение
первообразной аналитической функции
аналогично определению первообразной
функции действительной переменной).
И это позволяет сделать вывод о справедливости формулы Ньютона-Лейбница:
,
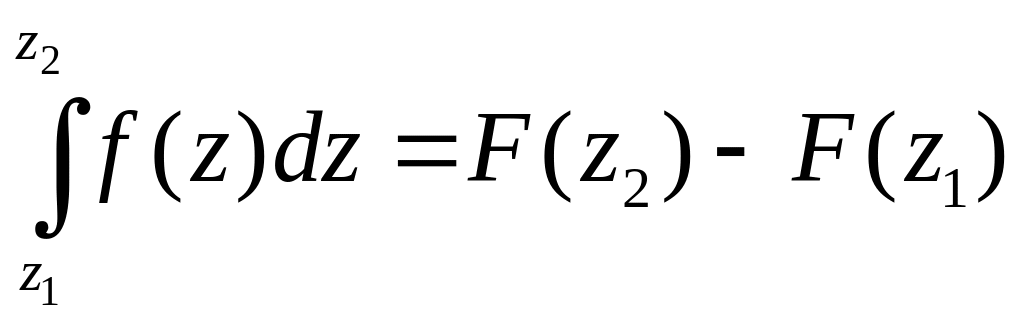здесь
- одна из первообразных функции
,
(
).
Этот
результат позволяет сводить вычисление
интеграла от аналитической функции
к отысканию какой-либо первообразной
функции и, следовательно, использовать
известные формулы и методы интегрирования
функций действительной переменной. В
частности, если
и
аналитические функции, то будет
справедлива формула
интегрирования по частям:
.
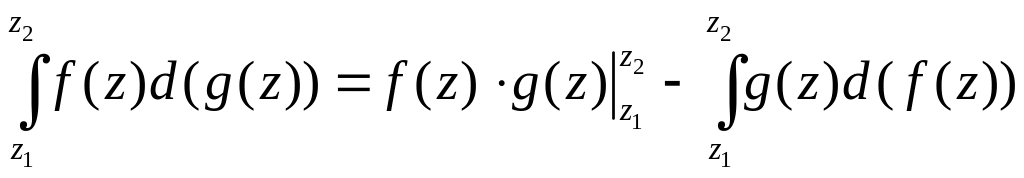Пример.
Вычислить интеграл
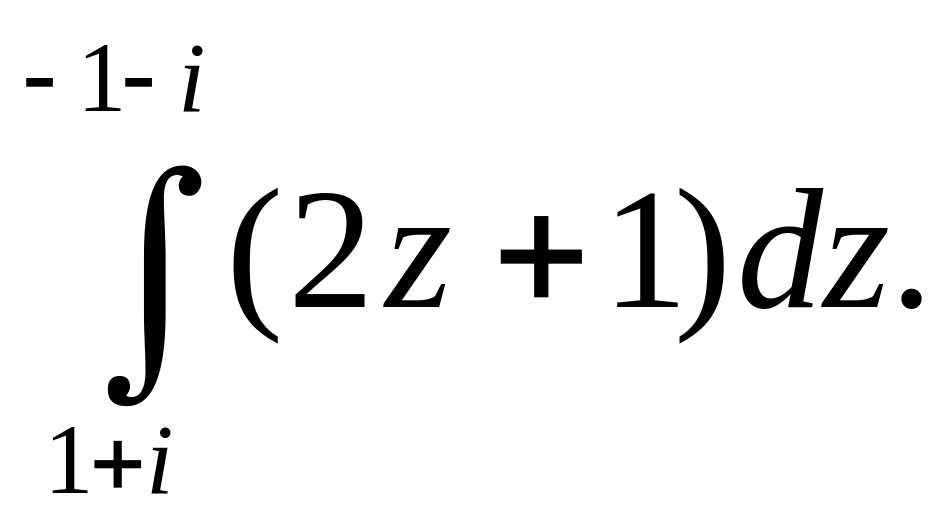
Решение. Подынтегральная функция является аналитической на всей комплексной плоскости, поэтому для нее существует первообразная. Воспользуемся формулой Ньютона-Лейбница:
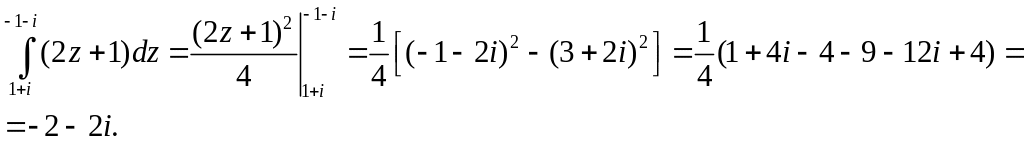
Пример.
Вычислить
интеграл
.
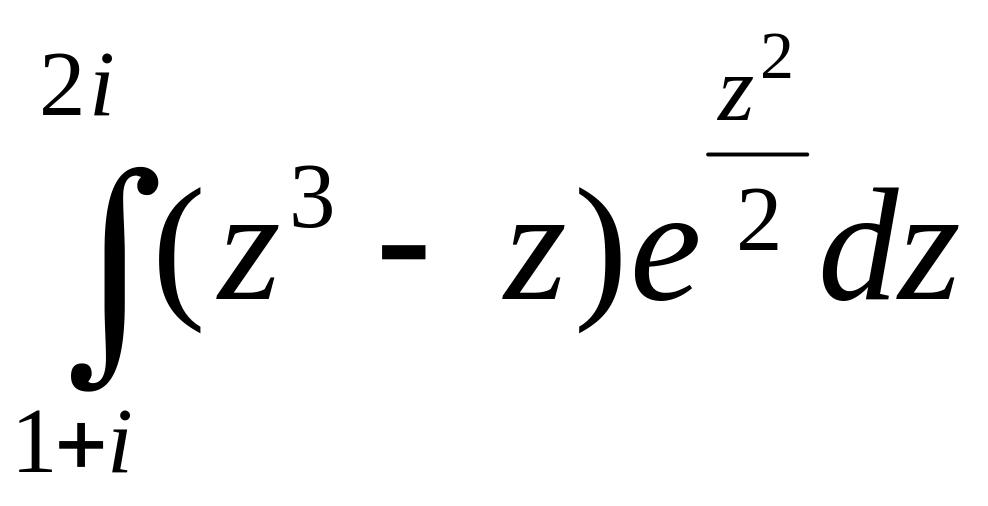Решение. Подынтегральная функция является аналитической, поэтому воспользуемся формулой интегрирования по частям:
=
=
=
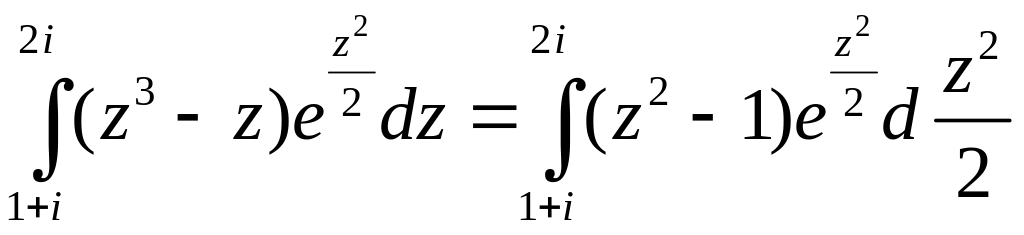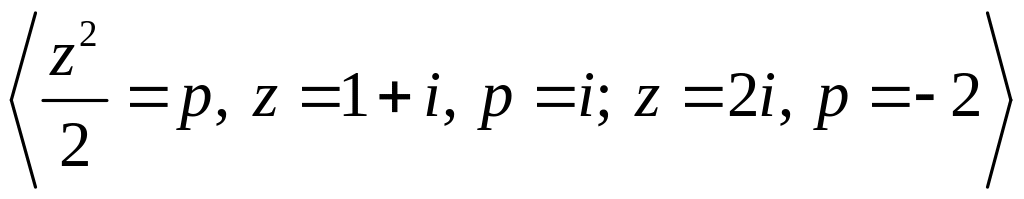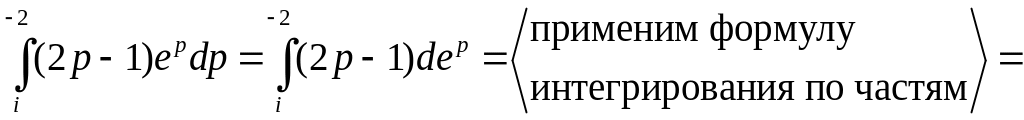
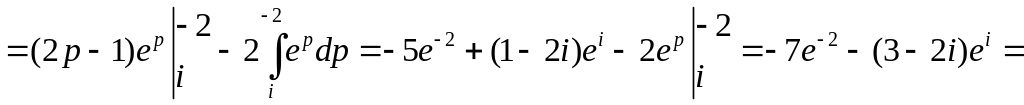
Аналитические функции комплексного переменного обладают следующим замечательным свойством:
Теорема 3. (Интегральная формула Коши) Если - внутренняя точка односвязной области , ограниченной замкнутым контуром , - аналитическая в замкнутой области функция, то справедлива формула:
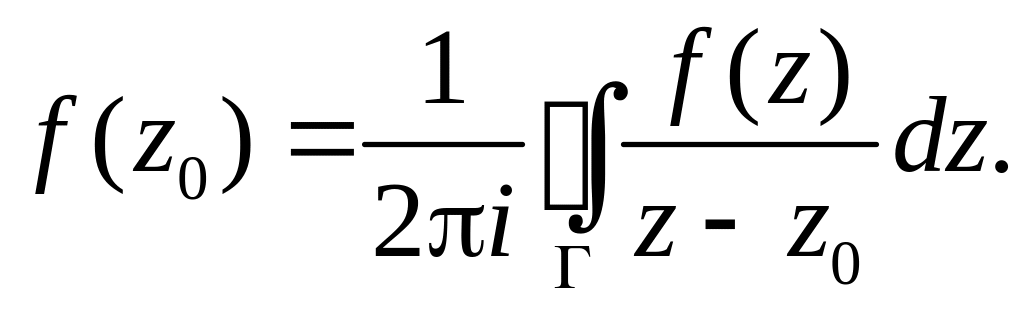
Иными словами, если мы знаем значение аналитической функции на границе односвязной области, то мы можем найти значение этой функции в любой внутренней точке области.
Более того, справедлива следующая теорема.
Теорема 4. Если однозначная функция комплексного переменного имеет всюду в области первую производную, то она имеет в этой области и все производные высших порядков, которые могут быть найдены по формуле:
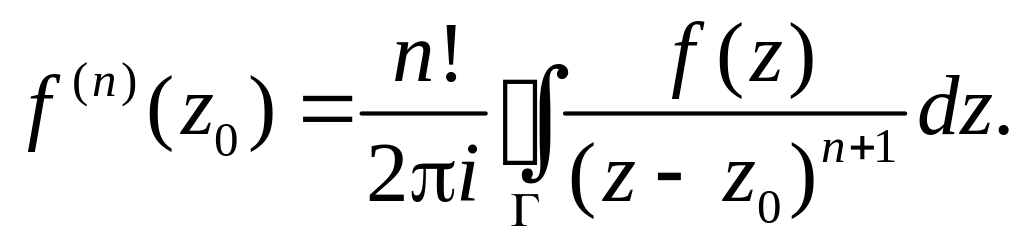
Интегральную формулу Коши и формулу для производных высших порядков можно использовать для вычисления интегралов по замкнутому контуру.
Пример.
Вычислить интеграл
.
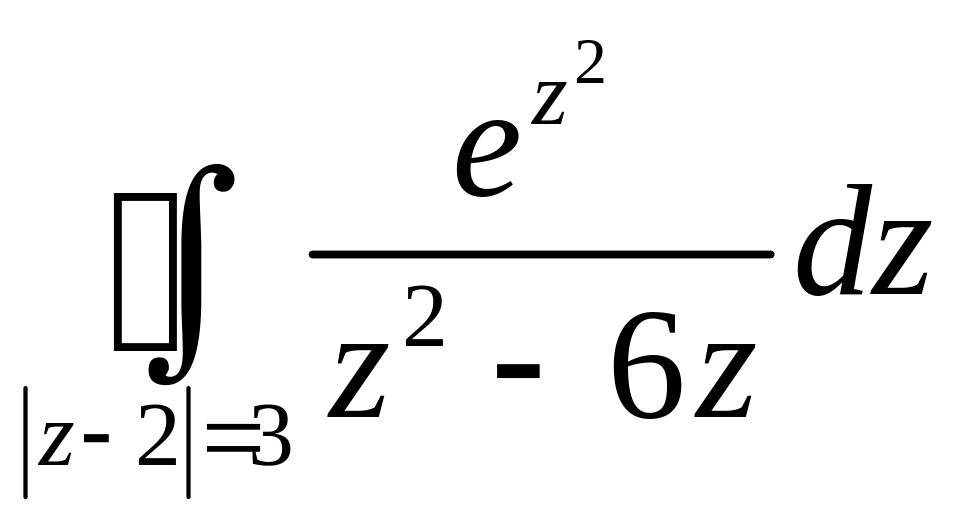Решение.
Рассмотрим подынтегральную функцию
.
Аналитичность этой функции нарушается
в точках:
(точки,
в которых знаменатель равен 0). Контур,
по которому вычисляется интеграл:
,
есть окружность с центром в точке
и радиусом 3. Внутри этого контура лежит
точка
,
поэтому внутри контура подынтегральная
функция не является аналитической.
Запишем эту функцию в виде:
.
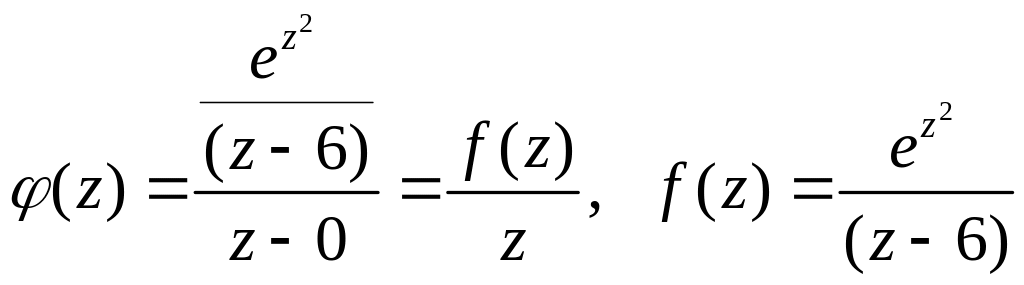Тогда функция
является
аналитической внутри замкнутого контура.
Воспользуемся интегральной формулой
Коши:
.
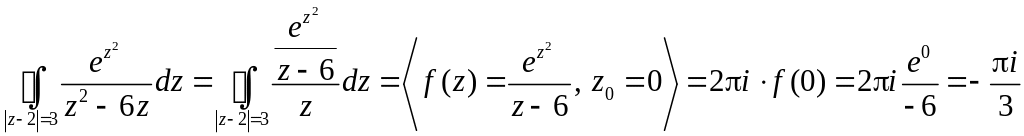Пример.
Вычислить интеграл
.
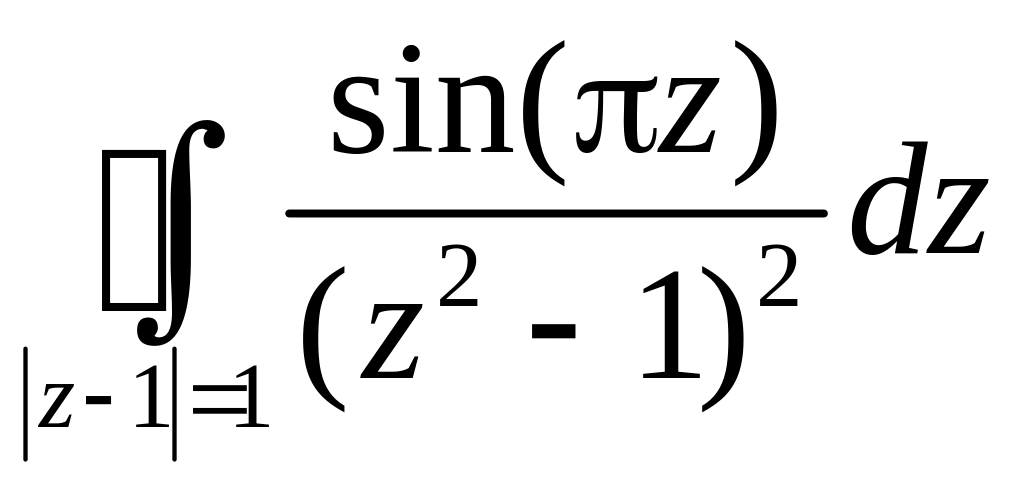Решение.
Аналитичность подынтегральной функции
нарушается в точках
.
Внутри контура есть только одна из них:
.
Преобразуем подынтегральную функцию
к виду:
.
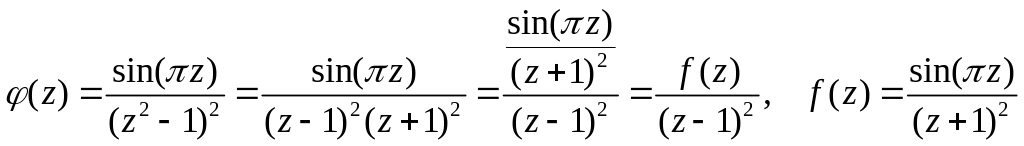Функция
-
аналитическая внутри контура, поэтому
можно применить теорему 4 (в данном
случае
):
