
- •Оглавление
- •Введение
- •1. Теория функций комплексного переменного
- •Комплексные числа и операции над ними
- •1.1.1. Определение комплексного числа
- •1.1.2. Формы записи комплексных чисел
- •1.1.3. Формула Муавра и извлечение корня n-ой степени из комплексного числа
- •1.2. Функции комплексного переменного
- •1.3. Дифференцирование функций комплексного переменного
- •1.3.1. Определение производной
- •1.3.2. Необходимые и достаточные условия дифференцируемости функции комплексного переменного
- •1.3.3. Производные основных элементарных функций
- •1.3.4. Восстановление аналитической функции по известной действительной или мнимой части
- •Интегрирование функций комплексного переменного
- •1.4.1. Определение интеграла от функции комплексного переменного
- •1.4.2. Теорема Коши. Вычисление интегралов от аналитических функций
- •2. Теория рядов
- •2.1. Числовые ряды
- •2.1.1.Основные понятия Пусть дана последовательность чисел (вещественных или комплексных)
- •Свойства сходящихся рядов
- •Замечание. Условие является необходимым, но не достаточным для сходимости, т.Е. Если , то ряд может сходиться, а может и расходиться.
- •Т. Е. Сходимость ряда равносильна тому, что сумма любого числа членов ряда, следующих за достаточно большим номером, должна быть произвольно мала.
- •2.1.2. Достаточные признаки сходимости положительных рядов
- •Пусть даны два положительных ряда и .
- •2.1.3. Сходимость рядов с произвольными членами
- •2.2. Функциональные ряды
- •2.2.1. Сходимость функционального ряда
- •Функциональные свойства суммы сходящегося ряда
- •2.2.2. Степенные ряды
- •Область сходимости степенных рядов
- •Ряды Тейлора и Маклорена
- •2.3. Ряды Фурье
- •2.3.1. Тригонометрический ряд Фурье. Периодические функции.
- •2.3.2. Сходимость ряда Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода 2l
- •2.3.3. Интеграл Фурье
- •3. Теория вероятностей
- •Случайные события и их вероятности
- •Классификация событий
- •3.1.2. Операции над событиями
- •3.1.3. Аксиоматическое определение вероятности
- •Примеры вероятностных пространств
- •Конечное вероятностное пространство
- •2. Непрерывное вероятностное пространство
- •3.1.4. Условная вероятность. Теорема умножения вероятностей.
- •3.1.5. Формула полной вероятности. Формула Байеса
- •3.1.6. Последовательность независимых испытаний. Формула Бернулли
- •3.1.7. Статистическое определение вероятности
- •3.2. Случайные величины, их распределения и числовые
- •3.2.1.Дискретные случайные величины
- •3.2.2. Функция распределения. Плотность распределения
- •3.2.3. Математическое ожидание случайной величины
- •3.2.4. Дисперсия случайной величины
- •3.2.5. Примеры законов распределения случайных величин Дискретные случайные величины
- •1. Биномиальное распределение
- •2. Распределение Пуассона
- •3. Геометрическое распределение
- •4. Гипергеометрическое распределение
- •Непрерывные случайные величины
- •5. Равномерное распределение
- •6. Показательное распределение
- •7. Нормальное распределение
- •3.3. Системы случайных величин
- •3.3.1. Закон распределения системы случайных величин
- •Условный закон распределения
- •3.3.2. Числовые характеристики случайного вектора
- •3.3.3. Предельные теоремы теории вероятностей
- •4. Математическая статистика
- •4.1. Методы статистического описания результатов наблюдений
- •4.1.1. Статистическое распределение выборки
- •4.1.2. Эмпирическая функция распределения
- •4.2. Оценки параметров распределения
- •4.2.1.Точечные оценки параметров распределения
- •4.2.2. Интервальные оценки параметров распределения
- •4.3. Проверка статистических гипотез
- •4.4. Статистические оценки параметров линейной корреляционной зависимости (между двумя случайными величинами)
- •5. Контрольная работа № 7. Задания
- •5.1. Пример выполнения контрольной работы № 1. Вариант 0.
- •5.2. Варианты заданий контрольной работы № 7
- •6. Контрольная работа № 8. Задания
- •6.1. Пример выполнения контрольной работы № 2. Вариант № 0.
- •6.2. Варианты заданий контрольной работы № 8
1.2. Функции комплексного переменного
Пусть
![]() - некоторое множество комплексных чисел
(или множество точек комплексной
плоскости). Пусть комплексное число
может принимать любое значение из
,
тогда будем называть
- комплексным переменным, а
- областью его изменения.
- некоторое множество комплексных чисел
(или множество точек комплексной
плоскости). Пусть комплексное число
может принимать любое значение из
,
тогда будем называть
- комплексным переменным, а
- областью его изменения.
Определение.
Величина
![]() называется
функцией независимого переменного
,
если каждому
значению
соответствует
одно или несколько комплексных значений
,
при этом пишут:
называется
функцией независимого переменного
,
если каждому
значению
соответствует
одно или несколько комплексных значений
,
при этом пишут:
![]() .
.
Запишем комплексные числа и в алгебраической форме:
,
![]() .
.
Тогда
![]() ,
и значит, задание функции комплексного
переменного
,
и значит, задание функции комплексного
переменного
![]() эквивалентно заданию двух действительных
функций от двух действительных переменных.
эквивалентно заданию двух действительных
функций от двух действительных переменных.
Определение.
Число
![]() называется пределом функции
называется пределом функции
![]() при
при
![]() ,
если для любого
,
если для любого
![]() найдется такое
найдется такое
![]() ,
что
,
что
![]() как только
как только
![]() (
(![]() ).
Записывают:
).
Записывают:
![]() .
.
Несложно показать, что соотношение ,
где
![]() ,
а
,
а
![]() ,
,
![]() эквивалентно двум действительным
соотношениям:
эквивалентно двум действительным
соотношениям:
![]() .
.
Определение.
Функция
называется непрерывной
в точке
![]() ,
если она определена в некоторой
окрестности этой точки и
,
если она определена в некоторой
окрестности этой точки и
![]() .
.
Если
,
определенная на множестве
,
непрерывна в каждой точке этого множества,
то говорят, что она непрерывна на
множестве
.
Вновь легко показать, что условие
непрерывности функции
в точке
эквивалентно двум соотношениям:
![]() .
Таким образом, функция комплексного
переменного непрерывна в точке
тогда и только тогда, когда ее действительная
и мнимая части, рассматриваемые как
функции действительных переменных
.
Таким образом, функция комплексного
переменного непрерывна в точке
тогда и только тогда, когда ее действительная
и мнимая части, рассматриваемые как
функции действительных переменных
![]() и
и
![]() ,
непрерывны в той же точке.
,
непрерывны в той же точке.
Введем определения основных элементарных функций комплексного переменного.
Показательная
функция
![]() .
.
Определение.
Функция
для
комплексных значений z=x+iy
определяется формулой:
![]() .
.
Следовательно,
![]()
Свойства функции :
Для любых
 и
и
 справедливо:
справедливо:
 .
.Функция
 периодична с периодом
периодична с периодом
 :
:
 .
.Функция непрерывна на всей комплексной области.
Для любого имеют место равенства:

Функция принимает все значения, кроме нуля, т.е. уравнение
 разрешимо для любого комплексного
разрешимо для любого комплексного .
.
Тригонометрические функции.
Тригонометрические функции комплексного аргумента определяются формулами:
 ,
,
 .
.
Свойства тригонометрических функций:
функции
 непрерывны на всей комплексной плоскости,
непрерывны на всей комплексной плоскости,функции принимают все значения, т.е. уравнения
 и
и
 имеют решения для любого комплексного
числа
имеют решения для любого комплексного
числа
 .
.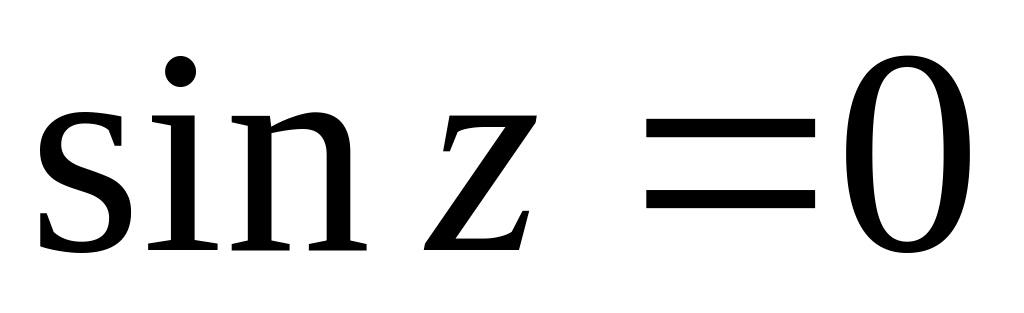 при
при
 ;
; при
при
 .
.все формулы элементарной тригонометрии, справедливые для всех действительных чисел, остаются справедливыми и при всех комплексных значениях z.
Например:
![]() ,
,
![]() ,
,
![]() .
.
функции являются периодическими с периодом :

функция
 -
нечетная функция,
-
нечетная функция,
 ;
функция
;
функция
 -
четная функция,
-
четная функция,
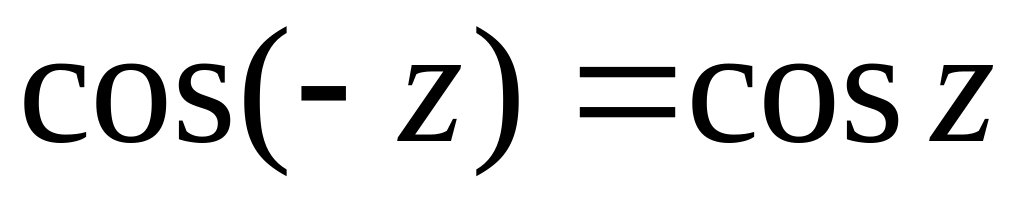 .
.функция
 непрерывна при
непрерывна при
 ,
функция
,
функция
 непрерывна при
непрерывна при
 .
.
Гиперболические функции
Гиперболические
функции
![]() определяются равенствами:
определяются равенствами:
![]() - гиперболический
синус (
- гиперболический
синус (![]() ),
),
![]() -
гиперболический
косинус (
-
гиперболический
косинус (![]() ),
),
 -
гиперболический
тангенс,
-
гиперболический
тангенс,
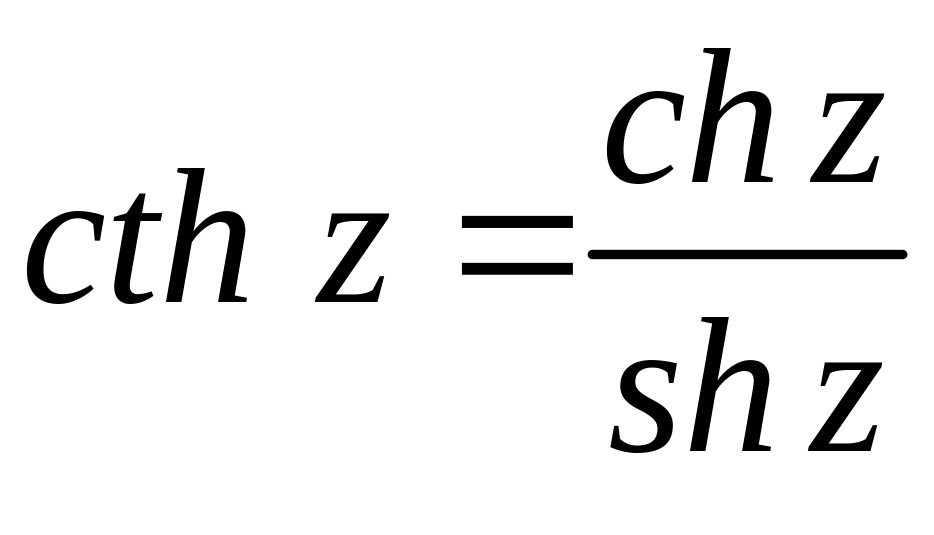 -
гиперболический
котангенс.
-
гиперболический
котангенс.
Свойства гиперболических функций вытекают из свойств функций и ; все формулы, справедливые при действительных значениях x, остаются справедливыми и для комплексных значений z.
Логарифмическая функция
Логарифмическая
функция
![]() определяется как функция обратная к
показательной.
определяется как функция обратная к
показательной.
Определение.
Если
![]() ,
где
,
где
![]() ,
то
называется логарифмом
числа
,
то
называется логарифмом
числа
z
и обозначается
![]()
Перепишем
равенство
в виде
![]() ,
тогда получим, что
,
тогда получим, что
![]() и
и
![]() .
.
Следовательно, логарифмическая функция задается равенством:
![]() ,
,
![]()
Логарифмическая
функция многозначна; ее ветвь,
соответствующую главному значению
аргумента
,
называют главным
значением логарифмической функции
и обозначают
![]() .
Таким образом,
.
Таким образом,
![]()
Свойства логарифмической функции:



 .
.
Обратные тригонометрические функции
Определение.
Если
![]() ,
то
называется арксинусом
числа z
и обозначается
,
то
называется арксинусом
числа z
и обозначается
![]()
Разрешая уравнение относительно , получим:
![]() .
.
Аналогично можно получить выражения для других обратных тригонометрических функций; все они выражаются через логарифмическую функцию:
![]() ,
,
![]() ,
,
![]() .
.
Пример.
Найти
![]()
Решение.
![]() ,
но
,
но
![]() ,
,
![]() и
поэтому
и
поэтому
![]() .
.
Пример.
Найти: а)![]() ,
б)
,
б)
![]()
Решение.
а) Поскольку
![]() ,
а главное значение аргумента у числа
-1 равно
,
а главное значение аргумента у числа
-1 равно
![]() ,
то получим:
=
,
то получим:
=![]() .
.
б)
по формуле
![]() получаем
получаем
![]()
Пример.
Найти
![]()
Решение.
По
определению функции
![]() получаем:
получаем:

Пример.
Записать в
алгебраической форме
![]()
Решение.![]() ,
тогда имеем
,
тогда имеем

![]()
