
- •Оглавление
- •Введение
- •1. Теория функций комплексного переменного
- •Комплексные числа и операции над ними
- •1.1.1. Определение комплексного числа
- •1.1.2. Формы записи комплексных чисел
- •1.1.3. Формула Муавра и извлечение корня n-ой степени из комплексного числа
- •1.2. Функции комплексного переменного
- •1.3. Дифференцирование функций комплексного переменного
- •1.3.1. Определение производной
- •1.3.2. Необходимые и достаточные условия дифференцируемости функции комплексного переменного
- •1.3.3. Производные основных элементарных функций
- •1.3.4. Восстановление аналитической функции по известной действительной или мнимой части
- •Интегрирование функций комплексного переменного
- •1.4.1. Определение интеграла от функции комплексного переменного
- •1.4.2. Теорема Коши. Вычисление интегралов от аналитических функций
- •2. Теория рядов
- •2.1. Числовые ряды
- •2.1.1.Основные понятия Пусть дана последовательность чисел (вещественных или комплексных)
- •Свойства сходящихся рядов
- •Замечание. Условие является необходимым, но не достаточным для сходимости, т.Е. Если , то ряд может сходиться, а может и расходиться.
- •Т. Е. Сходимость ряда равносильна тому, что сумма любого числа членов ряда, следующих за достаточно большим номером, должна быть произвольно мала.
- •2.1.2. Достаточные признаки сходимости положительных рядов
- •Пусть даны два положительных ряда и .
- •2.1.3. Сходимость рядов с произвольными членами
- •2.2. Функциональные ряды
- •2.2.1. Сходимость функционального ряда
- •Функциональные свойства суммы сходящегося ряда
- •2.2.2. Степенные ряды
- •Область сходимости степенных рядов
- •Ряды Тейлора и Маклорена
- •2.3. Ряды Фурье
- •2.3.1. Тригонометрический ряд Фурье. Периодические функции.
- •2.3.2. Сходимость ряда Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода 2l
- •2.3.3. Интеграл Фурье
- •3. Теория вероятностей
- •Случайные события и их вероятности
- •Классификация событий
- •3.1.2. Операции над событиями
- •3.1.3. Аксиоматическое определение вероятности
- •Примеры вероятностных пространств
- •Конечное вероятностное пространство
- •2. Непрерывное вероятностное пространство
- •3.1.4. Условная вероятность. Теорема умножения вероятностей.
- •3.1.5. Формула полной вероятности. Формула Байеса
- •3.1.6. Последовательность независимых испытаний. Формула Бернулли
- •3.1.7. Статистическое определение вероятности
- •3.2. Случайные величины, их распределения и числовые
- •3.2.1.Дискретные случайные величины
- •3.2.2. Функция распределения. Плотность распределения
- •3.2.3. Математическое ожидание случайной величины
- •3.2.4. Дисперсия случайной величины
- •3.2.5. Примеры законов распределения случайных величин Дискретные случайные величины
- •1. Биномиальное распределение
- •2. Распределение Пуассона
- •3. Геометрическое распределение
- •4. Гипергеометрическое распределение
- •Непрерывные случайные величины
- •5. Равномерное распределение
- •6. Показательное распределение
- •7. Нормальное распределение
- •3.3. Системы случайных величин
- •3.3.1. Закон распределения системы случайных величин
- •Условный закон распределения
- •3.3.2. Числовые характеристики случайного вектора
- •3.3.3. Предельные теоремы теории вероятностей
- •4. Математическая статистика
- •4.1. Методы статистического описания результатов наблюдений
- •4.1.1. Статистическое распределение выборки
- •4.1.2. Эмпирическая функция распределения
- •4.2. Оценки параметров распределения
- •4.2.1.Точечные оценки параметров распределения
- •4.2.2. Интервальные оценки параметров распределения
- •4.3. Проверка статистических гипотез
- •4.4. Статистические оценки параметров линейной корреляционной зависимости (между двумя случайными величинами)
- •5. Контрольная работа № 7. Задания
- •5.1. Пример выполнения контрольной работы № 1. Вариант 0.
- •5.2. Варианты заданий контрольной работы № 7
- •6. Контрольная работа № 8. Задания
- •6.1. Пример выполнения контрольной работы № 2. Вариант № 0.
- •6.2. Варианты заданий контрольной работы № 8
1.1.2. Формы записи комплексных чисел
Используя операции сложения и умножения комплексных чисел, запишем комплексное число в виде:
![]() .
.
Эта форма записи комплексного числа называется алгебраической формой.
Комплексные
числа, записанные в алгебраической
форме можно складывать и умножать как
обычные двучлены, учитывая, что
![]() .
.
Пример.
![]() .
.
Определение.
Два комплексных
числа
![]() и
и
![]() ,
которые отличаются знаком у мнимой
части, называют комплексно
сопряженными числами.
,
которые отличаются знаком у мнимой
части, называют комплексно
сопряженными числами.
Подчеркнем,
что
![]() .
.
Операцию
деления комплексных чисел,
записанных в алгебраической форме,
можно определить с помощью операции
умножения. А именно, чтобы вычислить
значение
![]() надо числитель и знаменатель дроби
умножить на число, сопряженное знаменателю:
надо числитель и знаменатель дроби
умножить на число, сопряженное знаменателю:
 .
.
Пример.
 .
.
Используя понятие модуля и аргумента комплексного числа можно записать:
![]() .
.
Эту форму записи называют тригонометрической формой записи комплексного числа.
Числа, записанные в тригонометрической форме, удобно умножать и делить, используя свойства модуля и аргумента.
Введем
обозначение
![]() (позже мы увидим, что введенный здесь
формально символ
(позже мы увидим, что введенный здесь
формально символ
![]() есть не что иное, как
есть не что иное, как
![]() ).
Тогда получим показательную
форму записи
комплексного числа:
).
Тогда получим показательную
форму записи
комплексного числа:
![]() .
.
Таким образом, всякое комплексное число можно записать в трех формах:
![]() .
.
В силу указанных свойств модуля и аргумента, операции умножения и деления комплексных чисел удобнее выполнять, если эти числа записаны в тригонометрической или показательной форме.
Пример.
Записать комплексное число
![]() в трех формах записи.
в трех формах записи.
Решение.
![]() - алгебраическая форма записи.
- алгебраическая форма записи.
![]() ,
,
![]() ,
,
![]() -
тригонометрическая форма записи,
-
тригонометрическая форма записи,
![]() -
показательная форма записи.
-
показательная форма записи.
Пример.
Вычислить
![]() ,
если
,
если
![]() ,
,
![]() .
.
Решение.
Запишем данные комплексные числа в
показательной форме.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
 ,
,
 .
Тогда
.
Тогда
 .
.
1.1.3. Формула Муавра и извлечение корня n-ой степени из комплексного числа
Свойства модуля и аргумента комплексного числа позволяют получить формулу возведения комплексного числа в целую положительную степень:
![]() -
эту формулу называют формулой
Муавра.
-
эту формулу называют формулой
Муавра.
Или
в показательной форме
![]() .
.
Легко
проверить, что эта формула остается
справедливой и для
![]() ,
и для целых отрицательных степеней.
,
и для целых отрицательных степеней.
Пример.
Найти
![]()
Решение.
Запишем сначала число
![]() в тригонометрической форме:
в тригонометрической форме:
![]() ,
,
 .
.
По формуле Муавра имеем:
![]() Определение.
Корнем
n-ой
степени из
комплексного числа
Определение.
Корнем
n-ой
степени из
комплексного числа
![]() называется такое комплексное число
называется такое комплексное число
![]() ,
для которого:
,
для которого:
![]() .
.
Из
определения и формулы Муавра ясно, что
модуль искомого корня будет
![]() ,
а аргумент
,
а аргумент
![]() ,
где
,
где
![]() .
Таким образом,
.
Таким образом,
![]()
или
![]() .
.
Придавать
«k»
значения, большие, чем
![]() не имеет смысла, так как будем получать
уже имеющиеся значения аргумента (с
точностью до
не имеет смысла, так как будем получать
уже имеющиеся значения аргумента (с
точностью до
![]() ).
Следовательно, корень
n-ой
степени из
комплексного числа имеет n
различных значений, модули которых
одинаковы (
),
а аргументы двух последовательных
значений отличаются на угол
).
Следовательно, корень
n-ой
степени из
комплексного числа имеет n
различных значений, модули которых
одинаковы (
),
а аргументы двух последовательных
значений отличаются на угол
![]() .
Таким образом, все значения корня лежат
на окружности с центром в начале координат
радиуса
.
.
Таким образом, все значения корня лежат
на окружности с центром в начале координат
радиуса
.
Пример.
Вычислить
все значения корня
![]()
Решение.
![]() ,
,
![]() ,
,
![]() ,
,
 ,
,
![]() .
.
Ответ.
![]() ,
,
![]() .
.
Пример.
Найти все значения
![]() .
.
Решение.
Имеем
![]() ,
тогда
,
тогда
![]() .
.
Ответ.
 ,
,
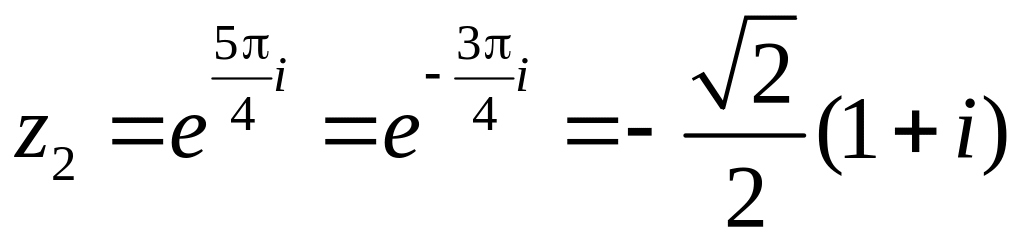 .
.
