
- •Оглавление
- •Введение
- •1. Теория функций комплексного переменного
- •Комплексные числа и операции над ними
- •1.1.1. Определение комплексного числа
- •1.1.2. Формы записи комплексных чисел
- •1.1.3. Формула Муавра и извлечение корня n-ой степени из комплексного числа
- •1.2. Функции комплексного переменного
- •1.3. Дифференцирование функций комплексного переменного
- •1.3.1. Определение производной
- •1.3.2. Необходимые и достаточные условия дифференцируемости функции комплексного переменного
- •1.3.3. Производные основных элементарных функций
- •1.3.4. Восстановление аналитической функции по известной действительной или мнимой части
- •Интегрирование функций комплексного переменного
- •1.4.1. Определение интеграла от функции комплексного переменного
- •1.4.2. Теорема Коши. Вычисление интегралов от аналитических функций
- •2. Теория рядов
- •2.1. Числовые ряды
- •2.1.1.Основные понятия Пусть дана последовательность чисел (вещественных или комплексных)
- •Свойства сходящихся рядов
- •Замечание. Условие является необходимым, но не достаточным для сходимости, т.Е. Если , то ряд может сходиться, а может и расходиться.
- •Т. Е. Сходимость ряда равносильна тому, что сумма любого числа членов ряда, следующих за достаточно большим номером, должна быть произвольно мала.
- •2.1.2. Достаточные признаки сходимости положительных рядов
- •Пусть даны два положительных ряда и .
- •2.1.3. Сходимость рядов с произвольными членами
- •2.2. Функциональные ряды
- •2.2.1. Сходимость функционального ряда
- •Функциональные свойства суммы сходящегося ряда
- •2.2.2. Степенные ряды
- •Область сходимости степенных рядов
- •Ряды Тейлора и Маклорена
- •2.3. Ряды Фурье
- •2.3.1. Тригонометрический ряд Фурье. Периодические функции.
- •2.3.2. Сходимость ряда Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода 2l
- •2.3.3. Интеграл Фурье
- •3. Теория вероятностей
- •Случайные события и их вероятности
- •Классификация событий
- •3.1.2. Операции над событиями
- •3.1.3. Аксиоматическое определение вероятности
- •Примеры вероятностных пространств
- •Конечное вероятностное пространство
- •2. Непрерывное вероятностное пространство
- •3.1.4. Условная вероятность. Теорема умножения вероятностей.
- •3.1.5. Формула полной вероятности. Формула Байеса
- •3.1.6. Последовательность независимых испытаний. Формула Бернулли
- •3.1.7. Статистическое определение вероятности
- •3.2. Случайные величины, их распределения и числовые
- •3.2.1.Дискретные случайные величины
- •3.2.2. Функция распределения. Плотность распределения
- •3.2.3. Математическое ожидание случайной величины
- •3.2.4. Дисперсия случайной величины
- •3.2.5. Примеры законов распределения случайных величин Дискретные случайные величины
- •1. Биномиальное распределение
- •2. Распределение Пуассона
- •3. Геометрическое распределение
- •4. Гипергеометрическое распределение
- •Непрерывные случайные величины
- •5. Равномерное распределение
- •6. Показательное распределение
- •7. Нормальное распределение
- •3.3. Системы случайных величин
- •3.3.1. Закон распределения системы случайных величин
- •Условный закон распределения
- •3.3.2. Числовые характеристики случайного вектора
- •3.3.3. Предельные теоремы теории вероятностей
- •4. Математическая статистика
- •4.1. Методы статистического описания результатов наблюдений
- •4.1.1. Статистическое распределение выборки
- •4.1.2. Эмпирическая функция распределения
- •4.2. Оценки параметров распределения
- •4.2.1.Точечные оценки параметров распределения
- •4.2.2. Интервальные оценки параметров распределения
- •4.3. Проверка статистических гипотез
- •4.4. Статистические оценки параметров линейной корреляционной зависимости (между двумя случайными величинами)
- •5. Контрольная работа № 7. Задания
- •5.1. Пример выполнения контрольной работы № 1. Вариант 0.
- •5.2. Варианты заданий контрольной работы № 7
- •6. Контрольная работа № 8. Задания
- •6.1. Пример выполнения контрольной работы № 2. Вариант № 0.
- •6.2. Варианты заданий контрольной работы № 8
3.1.2. Операции над событиями
Пространство элементарных исходов - есть произвольное множество, а случайные события – его подмножества. Введем операции над событиями и свяжем с ними операции над множествами.
Определение.
Если при каждом осуществлении комплекса
условий, при котором происходит событие
A, происходит и
событие B, то
говорят, что A влечет
за собой B, или A
является частным случаем B
(обозначается
![]() ).
В этом случае, множество A
является подмножеством множества B.
).
В этом случае, множество A
является подмножеством множества B.
Определение.
Если
и
![]() ,
то говорят, что события A
и B равны:
,
то говорят, что события A
и B равны:
![]() .
В этом случае, множества A
и B совпадают.
.
В этом случае, множества A
и B совпадают.
Определение.
Суммой или объединением двух
событий A и B
называется событие (обозначается
![]() или
или
![]() ),
состоящее в появлении хотя бы одного
из них.
),
состоящее в появлении хотя бы одного
из них.
По индукции определяется сумма n событий:
![]() .
.
Операции сложения событий соответствует операция объединения множеств.
Определение.
Произведением или пересечением
двух событий A и B
называется событие (обозначается
![]() или
или
![]() ),
состоящее в том, что они произошли
одновременно.
),
состоящее в том, что они произошли
одновременно.
По
индукции произведение n
событий:
![]() ,
,
![]() означает событие, состоящее в появлении
всех событий
означает событие, состоящее в появлении
всех событий
![]() .
.
Операции перемножения событий соответствует оперция пересечения множеств.
Понятия суммы и произведения событий распространяются на бесконечные последовательности событий, в этих случаях соответственно применяют обозначения:
![]() ,
,
![]() .
.
Определение.
Разностью событий A
и B называется событие
(обозначается
![]() или
или
![]() ),
которое означает, что наступает событие
A и не происходит
событие B.
Разность множеств A
и B соответствует
разности событий.
),
которое означает, что наступает событие
A и не происходит
событие B.
Разность множеств A
и B соответствует
разности событий.
Определение.
Событие
![]() называют противоположным событию A;
событие
называют противоположным событию A;
событие
![]() означает, что A не
произошло. Множество, соответсвующее
событию
,
является дополнением к множеству A.
означает, что A не
произошло. Множество, соответсвующее
событию
,
является дополнением к множеству A.
Определение.
События A и B
называют несовместными, если в
результате эксперимента они не могут
произойти одновременно, т.е.
![]() .
Это соотношение означает, что множества
A и B
не пересекаются.
.
Это соотношение означает, что множества
A и B
не пересекаются.
Пример. Эксперимент состоит в подбрасывании игральной кости один раз.
Элементарный исход ={на верхней грани выпало к очков}. Пространство элементарных исходов состоит из шести элементов: . Рассмотрим события из примера 1:
А={выпало 5 очков}, B={число выпавших очков четное}.
Эти события рассматривают как подмножества множества , а именно:
![]() .
.
Опишем следующие
события:
![]() .
.
Событие
![]() состоит в том, что B
не произошло, значит
состоит в том, что B
не произошло, значит
![]() ={выпало
нечетное число очков };
={выпало
нечетное число очков };
Событие
![]() состоит в том, что A и
B произошли одновременно,
значит
состоит в том, что A и
B произошли одновременно,
значит
![]() -
невозможное событие, т.к. число 5 не
является четным. Это означает, что
события A и B
несовместные.
-
невозможное событие, т.к. число 5 не
является четным. Это означает, что
события A и B
несовместные.
Событие
![]() состоит в том, что произошло хотя бы
одно из событий A или
B, значит
состоит в том, что произошло хотя бы
одно из событий A или
B, значит
![]() ={выпало
четное число очков или пятерка} .
={выпало
четное число очков или пятерка} .
Событие
![]() состоит в том, что событие
состоит в том, что событие
![]() произошло, а событие A
нет.
произошло, а событие A
нет.
Таким образом,
![]() ={выпали
единица или тройка}.
={выпали
единица или тройка}.
3.1.3. Аксиоматическое определение вероятности
Пусть
-
пространство элементарных исходов,
![]() -
некоторое множество (система ) случайных
событий.
-
некоторое множество (система ) случайных
событий.
Определение.
Система
случайных событий называется алгеброй
событий, если выполнены условия: 1)
![]() ;
2) если
;
2) если
![]() ,
то
,
то
![]() ,
,
![]() ,
,
![]() .
.
Из этого
определения вытекает, что
![]() ,
,
![]() .
.
Определение.
Алгебра событий называется
![]() -
алгеброй, если из того, что
-
алгеброй, если из того, что
![]() ,
следует
,
следует
![]() .
.
Определение.
Числовая функция
![]() ,
определенная на алгебре событий
,
называется вероятностью, если
выполнены следующие аксиомы.
,
определенная на алгебре событий
,
называется вероятностью, если
выполнены следующие аксиомы.
Аксиома
1. Каждому событию
![]() ставится в соответствие неотрицательное
число
- его вероятность, т.е.
ставится в соответствие неотрицательное
число
- его вероятность, т.е.
![]() для любого
.
для любого
.
Аксиома
2. Вероятность достоверного события
равна единице:
![]() .
.
Аксиома
3. Вероятность суммы двух несовместных
событий равна сумме вероятностей этих
событий, т.е.
![]() ,
если
.
,
если
.
Аксиома
4. Для любой последовательности
событий из
такой, что
![]() и
и
![]() ,
справедливо равенство
,
справедливо равенство
![]() .
.
Определение.
Тройка
![]() ,
в которой
является
-
алгеброй и функция
удовлетворяет аксиомам 1-4, называется
вероятностным пространством.
,
в которой
является
-
алгеброй и функция
удовлетворяет аксиомам 1-4, называется
вероятностным пространством.
Простейшие следствия из аксиом вероятности:
Сумма вероятностей противоположных событий равна единице:
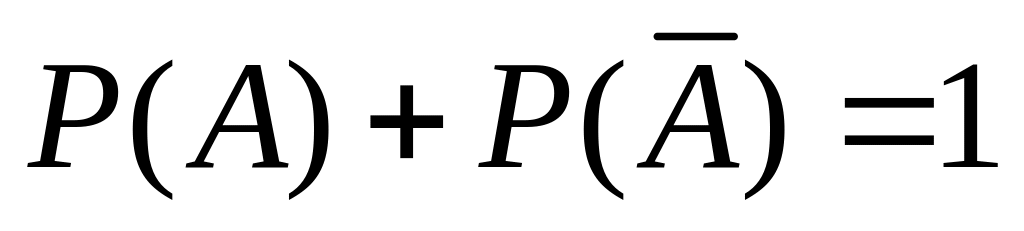 .
Тогда
.
Тогда
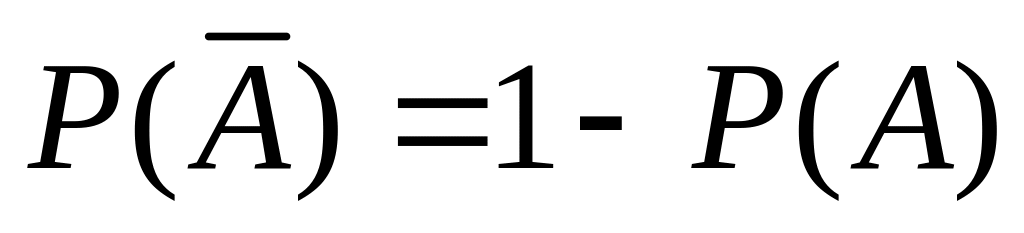 .
.Вероятность невозможного события равна нулю:
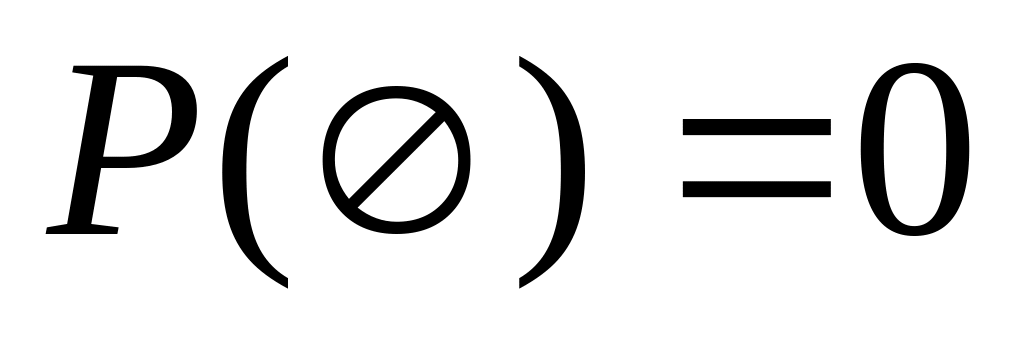 .
.Если событие A влечет событие B
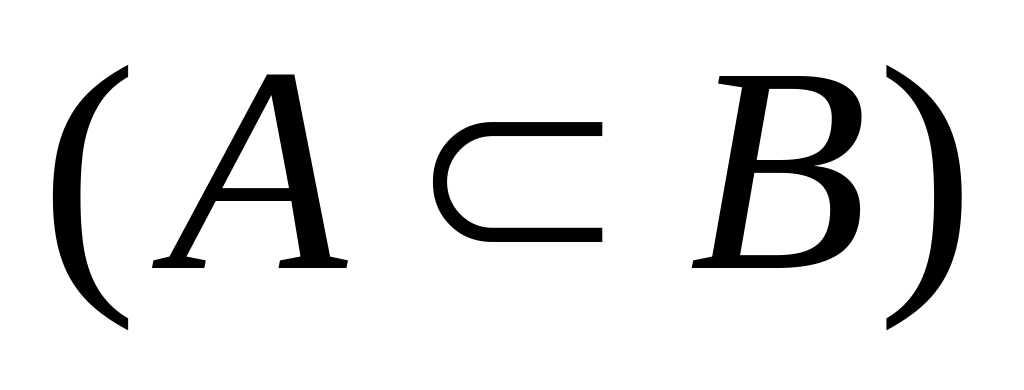 ,
то
,
то
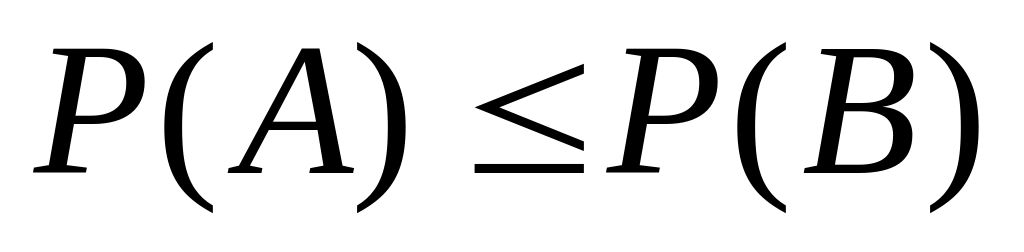 .
.Для любых событий A и B верны соотношения:
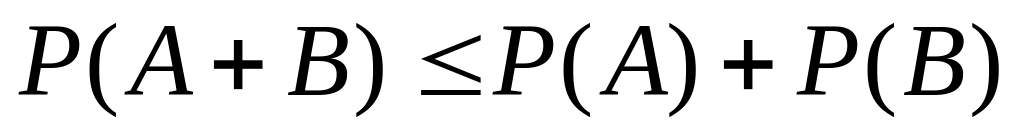 и
и
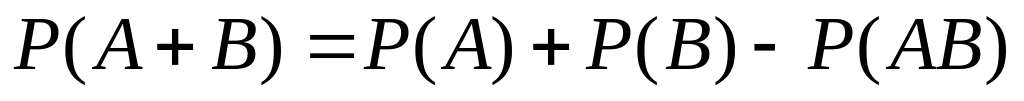 (Теорема сложения вероятностей).
(Теорема сложения вероятностей).Для любых событий
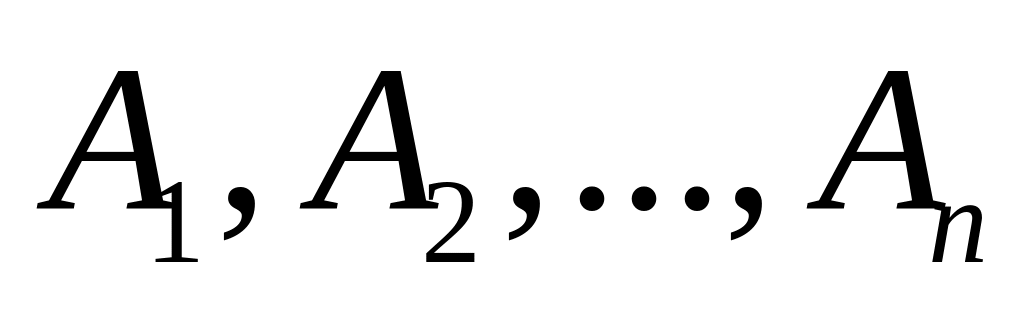 выполняется неравенство
выполняется неравенство
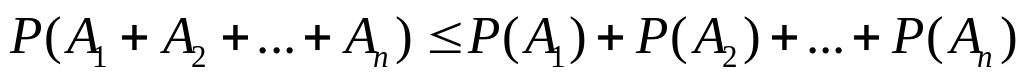 .
.Если события попарно несовместны (т.е.
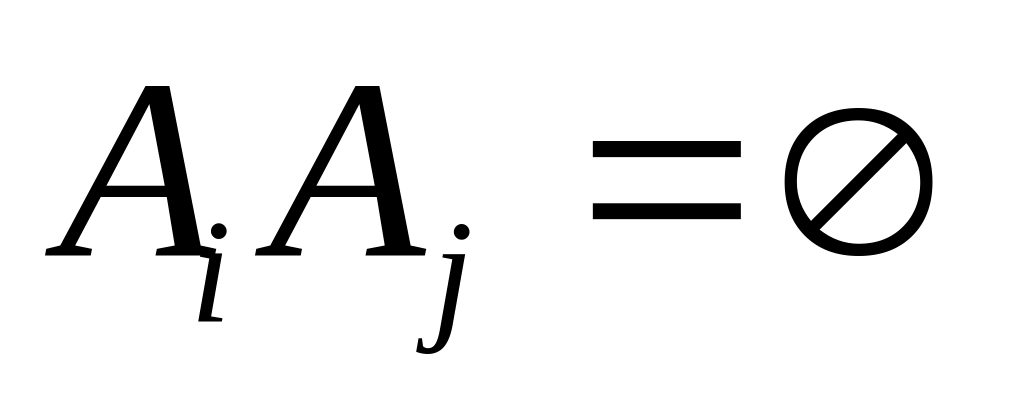 при любых
при любых
 ),
то
),
то
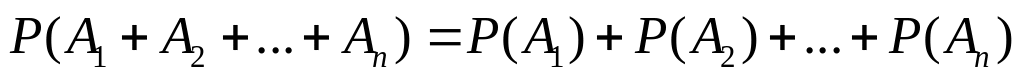 .
.Если события
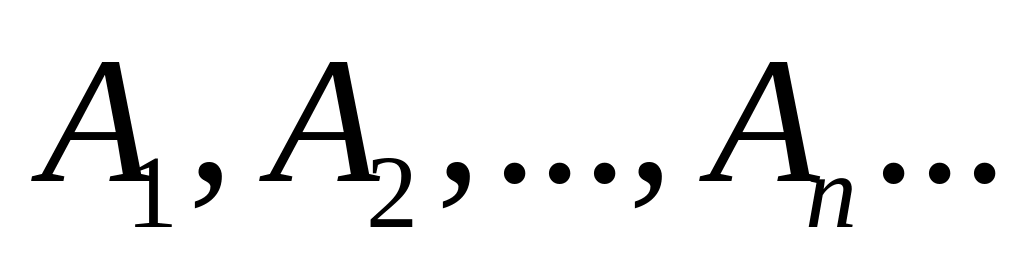 -
попарно несовместны и
-
попарно несовместны и
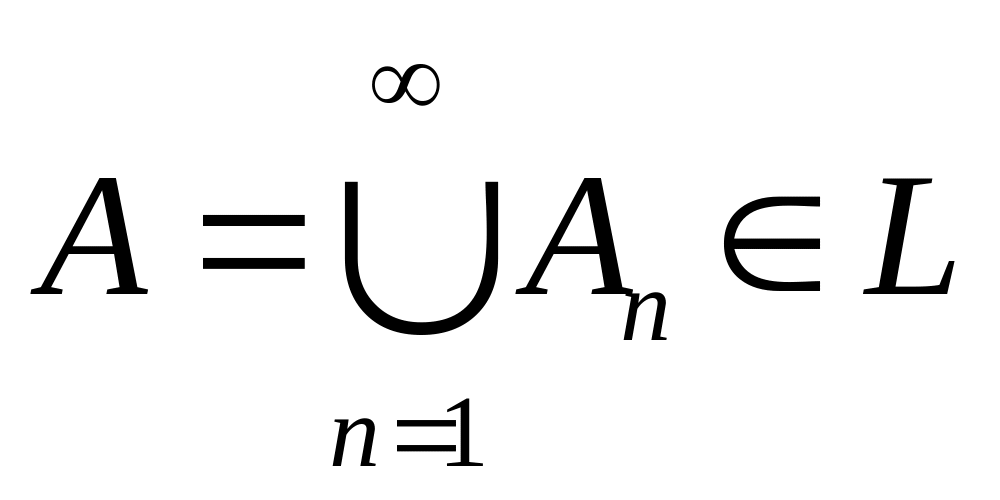 ,
то
,
то
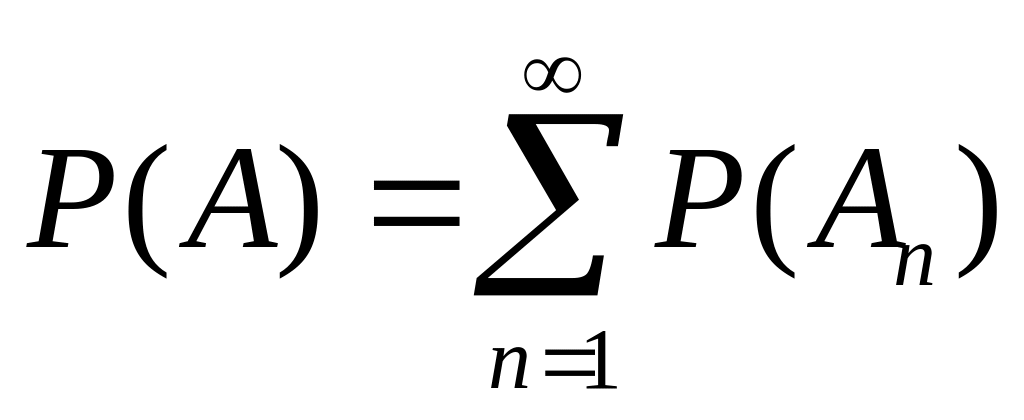 .
.Если и
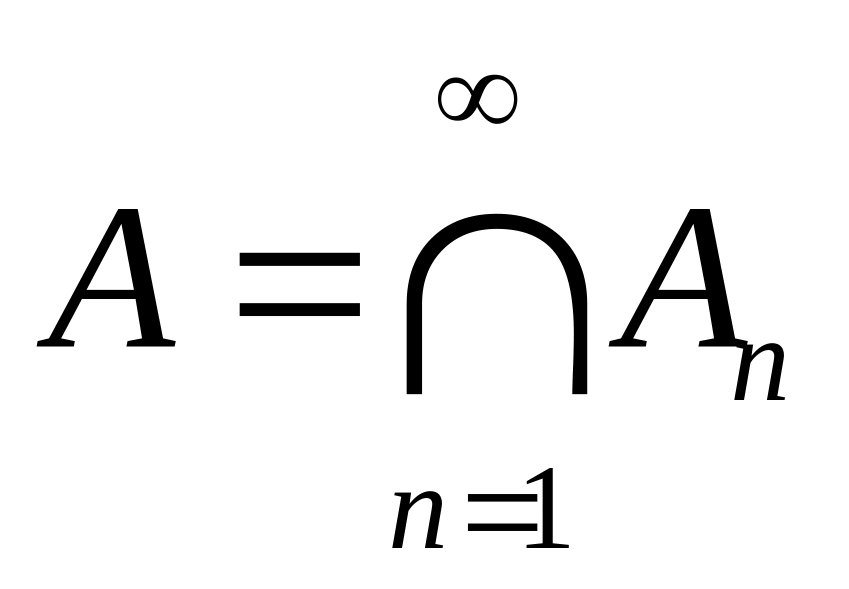 ,
то
,
то
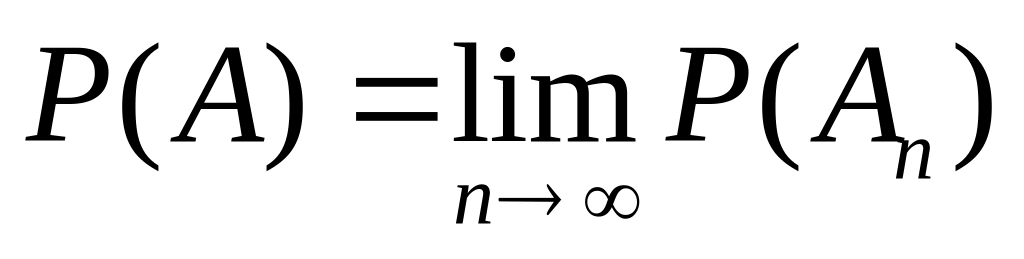 .
.
Если
![]() и
и
![]() ,
то
.
,
то
.
