
- •Оглавление
- •Введение
- •1. Теория функций комплексного переменного
- •Комплексные числа и операции над ними
- •1.1.1. Определение комплексного числа
- •1.1.2. Формы записи комплексных чисел
- •1.1.3. Формула Муавра и извлечение корня n-ой степени из комплексного числа
- •1.2. Функции комплексного переменного
- •1.3. Дифференцирование функций комплексного переменного
- •1.3.1. Определение производной
- •1.3.2. Необходимые и достаточные условия дифференцируемости функции комплексного переменного
- •1.3.3. Производные основных элементарных функций
- •1.3.4. Восстановление аналитической функции по известной действительной или мнимой части
- •Интегрирование функций комплексного переменного
- •1.4.1. Определение интеграла от функции комплексного переменного
- •1.4.2. Теорема Коши. Вычисление интегралов от аналитических функций
- •2. Теория рядов
- •2.1. Числовые ряды
- •2.1.1.Основные понятия Пусть дана последовательность чисел (вещественных или комплексных)
- •Свойства сходящихся рядов
- •Замечание. Условие является необходимым, но не достаточным для сходимости, т.Е. Если , то ряд может сходиться, а может и расходиться.
- •Т. Е. Сходимость ряда равносильна тому, что сумма любого числа членов ряда, следующих за достаточно большим номером, должна быть произвольно мала.
- •2.1.2. Достаточные признаки сходимости положительных рядов
- •Пусть даны два положительных ряда и .
- •2.1.3. Сходимость рядов с произвольными членами
- •2.2. Функциональные ряды
- •2.2.1. Сходимость функционального ряда
- •Функциональные свойства суммы сходящегося ряда
- •2.2.2. Степенные ряды
- •Область сходимости степенных рядов
- •Ряды Тейлора и Маклорена
- •2.3. Ряды Фурье
- •2.3.1. Тригонометрический ряд Фурье. Периодические функции.
- •2.3.2. Сходимость ряда Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода 2l
- •2.3.3. Интеграл Фурье
- •3. Теория вероятностей
- •Случайные события и их вероятности
- •Классификация событий
- •3.1.2. Операции над событиями
- •3.1.3. Аксиоматическое определение вероятности
- •Примеры вероятностных пространств
- •Конечное вероятностное пространство
- •2. Непрерывное вероятностное пространство
- •3.1.4. Условная вероятность. Теорема умножения вероятностей.
- •3.1.5. Формула полной вероятности. Формула Байеса
- •3.1.6. Последовательность независимых испытаний. Формула Бернулли
- •3.1.7. Статистическое определение вероятности
- •3.2. Случайные величины, их распределения и числовые
- •3.2.1.Дискретные случайные величины
- •3.2.2. Функция распределения. Плотность распределения
- •3.2.3. Математическое ожидание случайной величины
- •3.2.4. Дисперсия случайной величины
- •3.2.5. Примеры законов распределения случайных величин Дискретные случайные величины
- •1. Биномиальное распределение
- •2. Распределение Пуассона
- •3. Геометрическое распределение
- •4. Гипергеометрическое распределение
- •Непрерывные случайные величины
- •5. Равномерное распределение
- •6. Показательное распределение
- •7. Нормальное распределение
- •3.3. Системы случайных величин
- •3.3.1. Закон распределения системы случайных величин
- •Условный закон распределения
- •3.3.2. Числовые характеристики случайного вектора
- •3.3.3. Предельные теоремы теории вероятностей
- •4. Математическая статистика
- •4.1. Методы статистического описания результатов наблюдений
- •4.1.1. Статистическое распределение выборки
- •4.1.2. Эмпирическая функция распределения
- •4.2. Оценки параметров распределения
- •4.2.1.Точечные оценки параметров распределения
- •4.2.2. Интервальные оценки параметров распределения
- •4.3. Проверка статистических гипотез
- •4.4. Статистические оценки параметров линейной корреляционной зависимости (между двумя случайными величинами)
- •5. Контрольная работа № 7. Задания
- •5.1. Пример выполнения контрольной работы № 1. Вариант 0.
- •5.2. Варианты заданий контрольной работы № 7
- •6. Контрольная работа № 8. Задания
- •6.1. Пример выполнения контрольной работы № 2. Вариант № 0.
- •6.2. Варианты заданий контрольной работы № 8
2.3.2. Сходимость ряда Фурье
Теорема
1 (Дирихле).
Пусть
-
периодическая
функция
на отрезке
![]() удовлетворяет
двум условиям:
удовлетворяет
двум условиям:
1) кусочно – непрерывна (т.е. непрерывна или имеет конечное число точек разрыва 1 рода);
2) кусочно – монотонна (т.е. либо монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна).
Тогда ряд Фурье, соответствующий функции , сходится на этом отрезке и при этом:
-
в точках непрерывности функции сумма
ряда
совпадает
с самой функцией:
![]() ;
;
-
в каждой точке
![]() разрыва функции сумма ряда равна:
разрыва функции сумма ряда равна:
![]() ,
т.е. равна среднему арифметическому
пределов функции
справа и слева;
,
т.е. равна среднему арифметическому
пределов функции
справа и слева;
-
в точках
![]() и
и
![]() (на концах отрезка) сумма ряда равна
(на концах отрезка) сумма ряда равна
![]() .
.
Таким образом, если
-
периодическая функция
непрерывна на отрезке
,
то имеет место разложение :
![]() .
.
Разложение в ряд Фурье четных и нечетных функций
Если
функция
четная (т.е.
![]() ),
то все её коэффициенты
),
то все её коэффициенты
![]() ,
и ряд Фурье имеет вид
,
и ряд Фурье имеет вид
![]() ,
,
где
![]() ,
,
![]() .
.
Если
функция
нечетная (т.е.
![]() ),
то все коэффициенты
),
то все коэффициенты
![]() ,
и её ряд Фурье имеет вид
,
и её ряд Фурье имеет вид
![]() ,
,
где
![]() .
.
Определение. Эти ряды называются неполными тригонометрическими рядами, или рядами по косинусам и по синусам соответственно.
Разложение в ряд Фурье функций произвольного периода 2l
Пусть
функция
определена на отрезке
![]() и удовлетворяет на этом отрезке условиям
теоремы Дирихле. Введем новую переменную
по формуле
и удовлетворяет на этом отрезке условиям
теоремы Дирихле. Введем новую переменную
по формуле
![]() и рассмотрим функцию
и рассмотрим функцию
![]() .
Функция
.
Функция
![]() определена на отрезке
определена на отрезке
![]() и удовлетворяет теореме Дирихле. Ее ряд
Фурье имеет вид:
и удовлетворяет теореме Дирихле. Ее ряд
Фурье имеет вид:
![]() ,
,
где
![]() .
.
Вернемся к старой
переменной
![]() .
.
Определение.
Ряд
![]()
с коэффициентами, вычисляемыми по формулам
![]() ,
,
![]() ,
,
![]()
называется рядом
Фурье для функции
с периодом
![]() .
.
Замечание.
Если
на отрезке
![]() четная, то ее ряд Фурье имеет вид:
четная, то ее ряд Фурье имеет вид:
![]() ,
где
,
где
![]() ,
;
,
;
Если
-
нечетная функция, то
![]() ,
,
где
![]() ,
.
,
.
Пример.
Разложить в ряд Фурье
-
периодическую функцию, заданную
на промежутке
следующим образом:
 .
.
Решение. Построим график функции (Рис. 2).

Рис. 2
Данная
функция имеет конечное число разрывов
первого рода на промежутке
![]() .
По теореме Дирихле ее можно разложить
в ряд Фурье
.
По теореме Дирихле ее можно разложить
в ряд Фурье
![]() .
.
Вычислим коэффициенты Фурье:
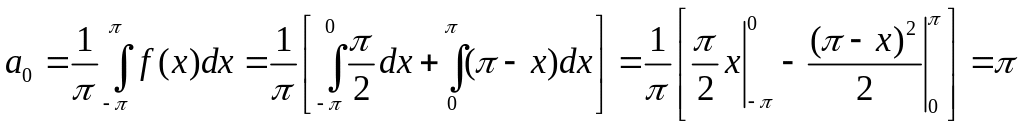 ;
; .
.
Ко второму интегралу применим формулу интегрирования по частям:
 .
.
Тогда
 =
=![]() =
=
=
=![]() .
.
Коэффициенты
с четным индексом обращаются в нуль, а
с нечетным, когда
![]() :
:
![]() .
.
Определим
коэффициенты
![]() :
:
 .
.
Проведя
вычисления аналогичным образом, получим
![]() .
Из всех коэффициентов
ненулевыми будут коэффициенты с четным
индексом
.
Из всех коэффициентов
ненулевыми будут коэффициенты с четным
индексом
![]() :
:
![]() .
Поставим найденные коэффициенты в ряд
Фурье
.
Поставим найденные коэффициенты в ряд
Фурье
![]() .
.
По
теореме Дирихле составленный ряд Фурье
сходится к функции
,
которая совпадает с
во всех точках ее непрерывности. Поэтому
знак
![]() можно
заменить знаком равенства:
можно
заменить знаком равенства:
![]() ,
,
![]()
В точках
разрыва функции
![]() сумма ряда
сумма ряда
 .
.
В точках
разрыва
![]() ,
,
 .
И так,
.
И так,
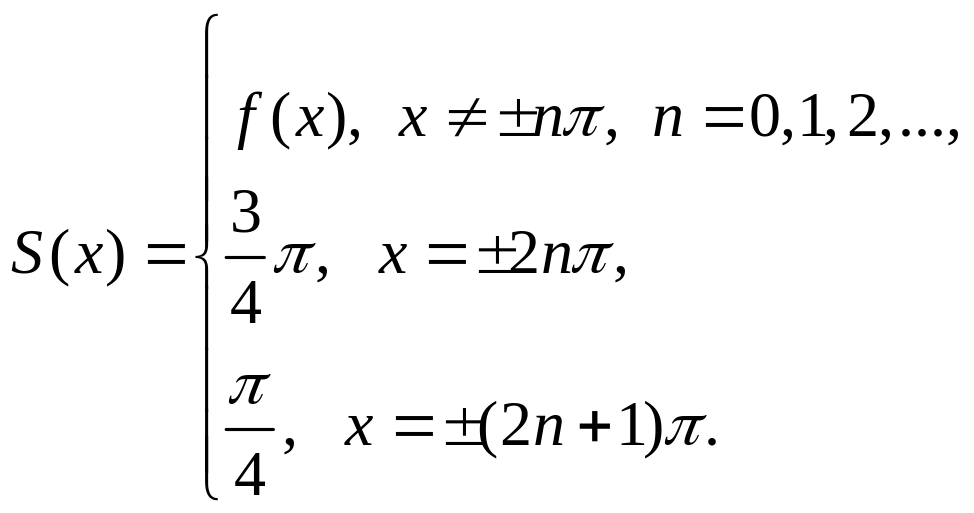
Пример.
Разложить в ряд Фурье
-
периодическую функцию, заданную
на промежутке
следующим образом:
![]() .
.
Рис.
3
Функция непрерывна на всей оси и может быть разложена в ряд Фурье, сходящийся к ней при всех , т.е. для любого . Так как - четная и , то .
Вычислим коэффициенты:
![]() ;
;
 =
= ,
т.е.
,
т.е.
![]() ,
,
![]() .
.
