
- •Оглавление
- •Введение
- •1. Теория функций комплексного переменного
- •Комплексные числа и операции над ними
- •1.1.1. Определение комплексного числа
- •1.1.2. Формы записи комплексных чисел
- •1.1.3. Формула Муавра и извлечение корня n-ой степени из комплексного числа
- •1.2. Функции комплексного переменного
- •1.3. Дифференцирование функций комплексного переменного
- •1.3.1. Определение производной
- •1.3.2. Необходимые и достаточные условия дифференцируемости функции комплексного переменного
- •1.3.3. Производные основных элементарных функций
- •1.3.4. Восстановление аналитической функции по известной действительной или мнимой части
- •Интегрирование функций комплексного переменного
- •1.4.1. Определение интеграла от функции комплексного переменного
- •1.4.2. Теорема Коши. Вычисление интегралов от аналитических функций
- •2. Теория рядов
- •2.1. Числовые ряды
- •2.1.1.Основные понятия Пусть дана последовательность чисел (вещественных или комплексных)
- •Свойства сходящихся рядов
- •Замечание. Условие является необходимым, но не достаточным для сходимости, т.Е. Если , то ряд может сходиться, а может и расходиться.
- •Т. Е. Сходимость ряда равносильна тому, что сумма любого числа членов ряда, следующих за достаточно большим номером, должна быть произвольно мала.
- •2.1.2. Достаточные признаки сходимости положительных рядов
- •Пусть даны два положительных ряда и .
- •2.1.3. Сходимость рядов с произвольными членами
- •2.2. Функциональные ряды
- •2.2.1. Сходимость функционального ряда
- •Функциональные свойства суммы сходящегося ряда
- •2.2.2. Степенные ряды
- •Область сходимости степенных рядов
- •Ряды Тейлора и Маклорена
- •2.3. Ряды Фурье
- •2.3.1. Тригонометрический ряд Фурье. Периодические функции.
- •2.3.2. Сходимость ряда Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода 2l
- •2.3.3. Интеграл Фурье
- •3. Теория вероятностей
- •Случайные события и их вероятности
- •Классификация событий
- •3.1.2. Операции над событиями
- •3.1.3. Аксиоматическое определение вероятности
- •Примеры вероятностных пространств
- •Конечное вероятностное пространство
- •2. Непрерывное вероятностное пространство
- •3.1.4. Условная вероятность. Теорема умножения вероятностей.
- •3.1.5. Формула полной вероятности. Формула Байеса
- •3.1.6. Последовательность независимых испытаний. Формула Бернулли
- •3.1.7. Статистическое определение вероятности
- •3.2. Случайные величины, их распределения и числовые
- •3.2.1.Дискретные случайные величины
- •3.2.2. Функция распределения. Плотность распределения
- •3.2.3. Математическое ожидание случайной величины
- •3.2.4. Дисперсия случайной величины
- •3.2.5. Примеры законов распределения случайных величин Дискретные случайные величины
- •1. Биномиальное распределение
- •2. Распределение Пуассона
- •3. Геометрическое распределение
- •4. Гипергеометрическое распределение
- •Непрерывные случайные величины
- •5. Равномерное распределение
- •6. Показательное распределение
- •7. Нормальное распределение
- •3.3. Системы случайных величин
- •3.3.1. Закон распределения системы случайных величин
- •Условный закон распределения
- •3.3.2. Числовые характеристики случайного вектора
- •3.3.3. Предельные теоремы теории вероятностей
- •4. Математическая статистика
- •4.1. Методы статистического описания результатов наблюдений
- •4.1.1. Статистическое распределение выборки
- •4.1.2. Эмпирическая функция распределения
- •4.2. Оценки параметров распределения
- •4.2.1.Точечные оценки параметров распределения
- •4.2.2. Интервальные оценки параметров распределения
- •4.3. Проверка статистических гипотез
- •4.4. Статистические оценки параметров линейной корреляционной зависимости (между двумя случайными величинами)
- •5. Контрольная работа № 7. Задания
- •5.1. Пример выполнения контрольной работы № 1. Вариант 0.
- •5.2. Варианты заданий контрольной работы № 7
- •6. Контрольная работа № 8. Задания
- •6.1. Пример выполнения контрольной работы № 2. Вариант № 0.
- •6.2. Варианты заданий контрольной работы № 8
Функциональные свойства суммы сходящегося ряда
По
функциональному ряду
построим последовательность частичных
сумм:
![]()
![]()
Определение.
Предел
последовательности частичных сумм
называют суммой
функционального ряда:
![]() .
Если при каждом
,
функциональный ряд сходится, то
.
Если при каждом
,
функциональный ряд сходится, то
![]() .
.
Определение.
Говорят, что
сходящийся функциональный ряд
равномерно
сходится на
отрезке
![]() к функции
к функции
![]() ,
если
для
,
если
для
![]() найдется не зависящий от x
номер
найдется не зависящий от x
номер
![]() такой, что при
выполняется неравенство
такой, что при
выполняется неравенство
![]() ,
,
![]() .
.
Теорема
1 (признак Вейерштрасса). Если
члены ряда
удовлетворяют неравенствам
![]() ,
где
,
где
![]() - члены сходящегося числового ряда
- члены сходящегося числового ряда
![]() ,
то ряд
сходится на
равномерно.
,
то ряд
сходится на
равномерно.
Теорема
2 (Непрерывность
суммы функционального ряда).
Пусть
![]() непрерывны
на отрезке
,
и ряд
сходится на
равномерно. Тогда сумма
этого
ряда непрерывна на
.
непрерывны
на отрезке
,
и ряд
сходится на
равномерно. Тогда сумма
этого
ряда непрерывна на
.
Теорема 3 (Почленный переход к пределу).
Если выполнены условия теоремы 2, то
для
существует предел суммы функционального
ряда
,
и он равен
![]() .
.
Теорема
4 (Почленное интегрирование). Пусть
![]() непрерывны, и пусть ряд
сходится на
равномерно. Тогда сумма ряда интегрируема,
причем
непрерывны, и пусть ряд
сходится на
равномерно. Тогда сумма ряда интегрируема,
причем
![]() .
.
Теорема
5 (Почленное дифференцирование). Пусть
![]() непрерывно-дифференцируемы на отрезке
,
и на этом отрезке ряды
и
непрерывно-дифференцируемы на отрезке
,
и на этом отрезке ряды
и
![]() сходятся
равномерно. Тогда сумма
ряда
имеет на
непрерывную производную, при этом
сходятся
равномерно. Тогда сумма
ряда
имеет на
непрерывную производную, при этом
![]() .
.
2.2.2. Степенные ряды
Определение. Степенным рядом называется функциональный ряд вида
![]()
где
![]() -
коэффициенты ряда (комплексные или
вещественные), а
-
коэффициенты ряда (комплексные или
вещественные), а
![]() - комплексная или
вещественная переменная.
- комплексная или
вещественная переменная.
Заменой
![]() ряд преобразуется к виду
ряд преобразуется к виду
![]()
Такой
ряд сходится, по крайней мере, в одной
точке:
![]() .
.
Теорема
6 (Теорема
Абеля).
Если степенной
ряд
![]() сходится в точке
сходится в точке
![]() ,
то он сходится абсолютно при
,
то он сходится абсолютно при
![]() и сходится равномерно при
и сходится равномерно при
![]() ,
где
,
где
![]() -
любое число из интервала
-
любое число из интервала
![]() .
Если этот ряд расходится в точке
.
Если этот ряд расходится в точке
![]() ,
то он расходится при
,
то он расходится при
![]() .
.
Область сходимости степенных рядов
Пусть М – множество всех , для которых ряд сходится.
Определение.
Число
![]() (конечное или бесконечное) называют
радиусом
сходимости
ряда.
(конечное или бесконечное) называют
радиусом
сходимости
ряда.
Если
![]() ,
то для всех
таких, что:
,
то для всех
таких, что:
![]() - ряд
абсолютно сходится, а если
- ряд
абсолютно сходится, а если
![]() ряд расходится. Если
ряд расходится. Если
![]() ,
то ряд абсолютно сходится при всех
.
,
то ряд абсолютно сходится при всех
.
Радиус
сходимости степенного ряда может быть
найден по одной из формул:
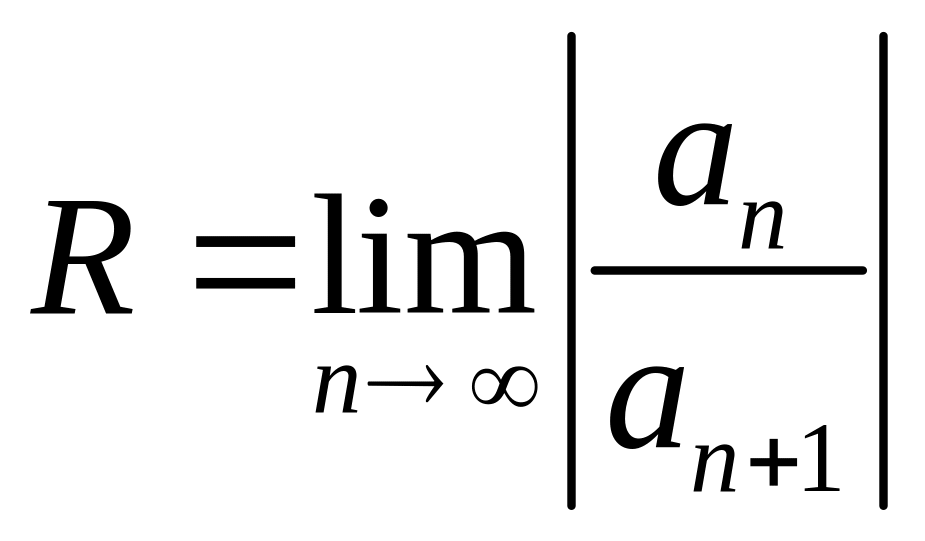 ,
или
,
или
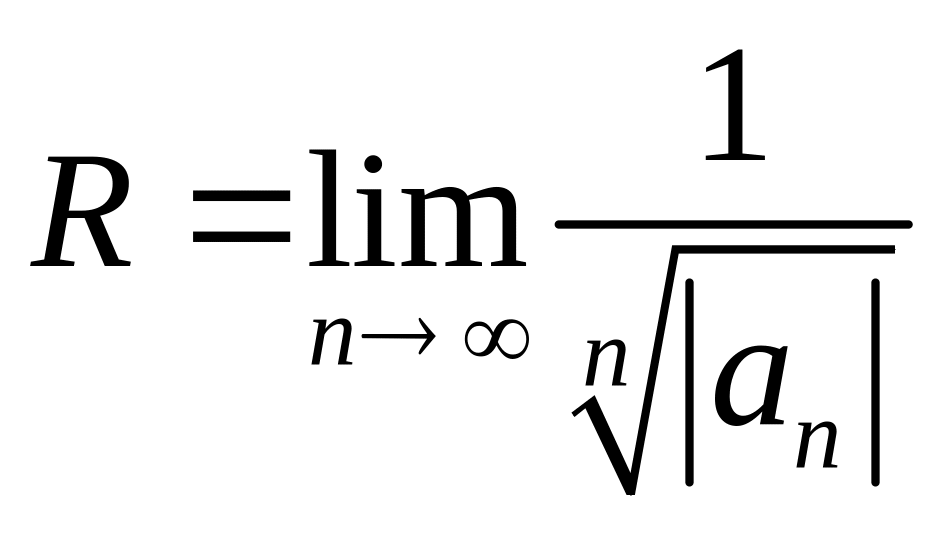 .
.
Пример.
Найти область
сходимости ряда
![]() .
.
Решение.
В данном случае коэффициенты степенного
ряда:
![]() .
Воспользуемся формулой
.
Воспользуемся формулой
=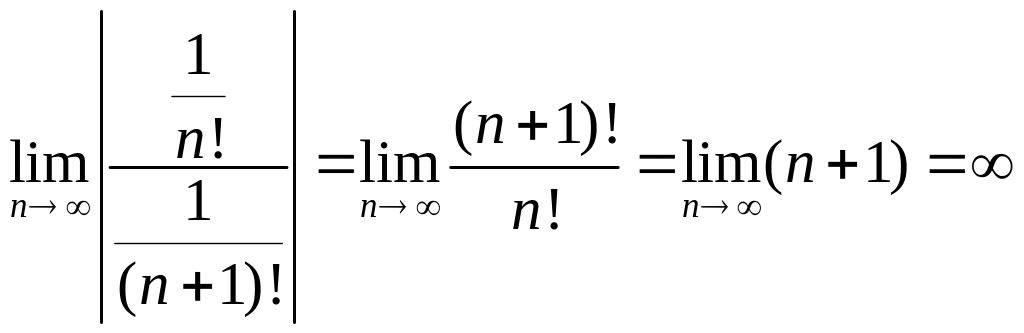 .
Отсюда следует, что данный ряд абсолютно
сходится на всей числовой оси.
.
Отсюда следует, что данный ряд абсолютно
сходится на всей числовой оси.
Пример.
Найти область
сходимости ряда
![]() .
.
Решение.
=![]() Для определения радиуса сходимости
удобно воспользоваться другой формулой:
Для определения радиуса сходимости
удобно воспользоваться другой формулой:
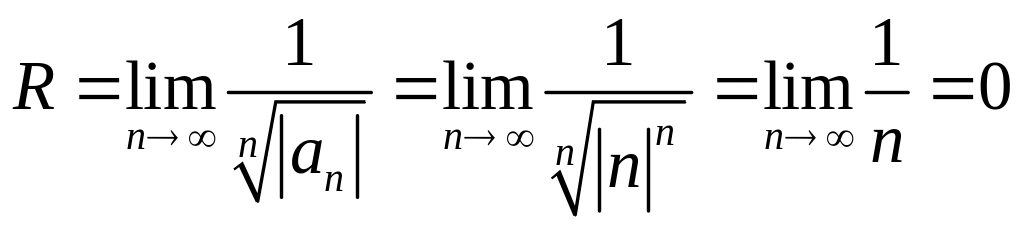 .
Значит, ряд сходится только в точке
и расходится при всех
.
Значит, ряд сходится только в точке
и расходится при всех
![]() .
.
Пример.
Найти область
сходимости ряда
![]() .
.
Решение.
=![]() .
.
Применим признак Даламбера к ряду из модулей членов функционального ряда .
![]() ;
;
![]() ;
;
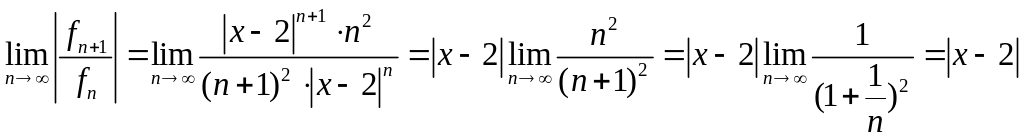 .
.
Тогда,
при
![]() ряд сходится, т.е. область сходимости:
ряд сходится, т.е. область сходимости:
![]() ,
,
![]() ,
есть интервал -
,
есть интервал -
![]() .
.
Если
![]() ,
имеем ряд
,
имеем ряд
![]() .
Этот ряд сходится как обобщеный
гармонический
при
.
Этот ряд сходится как обобщеный
гармонический
при
![]() .
.
Если
![]() ,
получаем ряд
,
получаем ряд
![]() .
Этот ряд сходится, так как сходится ряд
.
Этот ряд сходится, так как сходится ряд
![]() .
Значит, исходный ряд сходится при
.
Значит, исходный ряд сходится при
![]() .
.
