МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ФГБОУ ВПО «ВГТУ», ВГТУ)

КУРСОВАЯ РАБОТА

По дисциплине «Высшая математика»

Тема «Многочлены и их корни».

Выполнил студент АТ-101 К.И. Малюкова

Группа Подпись, инициалы, фамилия

дата

Руководитель В.С.Купцов

Подпись, инициалы, фамилия

дата

Защищена _______________________

Оценка________________________

Воронеж 2011

Оглавление

Введение…………………………………………………………………………..3

Теоретические сведения…………………………………………………………4

-пример задания…………………………………………………………...5

Практическая часть……………………………………………………………....9

Заключение………………………………………………………………………13

Библиографический список…………………………………………………….14

Введение

Дифференциальное уравнение широко используется для решения многих инженерных задач. Часто необходимо найти корни дифференциального уравнения или узнать и их расположение в зависимости от коэффициентов уравнений. Для решения дифференциальных уравнений и нахождения их коэффициентов используют характеристические уравнения и их корни. Поэтому эта курсовая работа посвящена взаимосвязи корней характеристического уравнения с коэффициентами и нахождения подобластей с различным характером поведения решения, соответствующей степени устойчивости.

Теоретические сведения

Функция

P(x) = a_nxⁿ + a_n-1x^n-1 + …+a₁x + a₀,

где n - целое число, называется многочленом от x степени n.

Число  называется корнем многочлена P(x), если Р()=0, иначе говоря   корень уравнения Р(х)=0.

Уравнение Р(х)=0, в котором Р(х)  многочлен степени n, называется алгебраическим уравнением степени n.

Всякое алгебраическое уравнение Р(х)=0 степени n имеет по крайней мере один корень (основная теорема алгебры) и не более n различных корней.

Остаток от деления многочлена Р(х) на разность (х-) равен Р(), т.е. значению Р(х) при х= (теорема Безу).

Если   корень многочлена Р(х) степени n, то этот многочлен делится на (х-) без остатка, т.е. представляется в виде произведения

Р(х) = (х - )Q(х),

где Q(х)  многочлен степени n-1.

Всякий многочлен n-й степени разлагается на n линейных сомножителей (х-₁),…,(х-_n), где ₁,…,_n  корни многочлена, и множитель, равный коэффициенту при хⁿ:

a_nxⁿ + a_n-1x^n-1 + …+a₁x + a₀ = a_n (х-₁)  (х-₂)… (х-_n),

причем часть или даже все корни  могут быть одинаковыми. Такие корни называются кратными.

Приравнивая в последнем уравнении коэффициенты при равных степенях х, получим выражения, связывающие коэффициенты многочлена с его корнями:

a_n-1 = -a_n(₁ + ₂ + … +_n);

a_n-2 = a_n(₁₂ + ₁₃ + … +_n-1 _n);

…………

a₀ = a_n(₁₂ … _n)(-1)ⁿ.

Эти выражения называются формулами Виета.

Пример задания

Для дифференциального уравнения

в плоскости его коэффициентов А и В найти область, соответствующую устойчивому решению y(t), выделив в ней подобласти с различным характером поведения решения при изменении аргумента t.

Решение.

Для анализа устойчивости решения y(t) дифференциального уравнения

составим характеристическое уравнение

s³+As²+Bs+1=0,

корни которого обозначим через s₁,s₂,s₃.

В соответствии с определением устойчивости по Ляпунову устойчивое решение y(t) будет получено, если все корни s₁,s₂ и s₃ будут иметь отрицательные вещественные части, т.е. будут располагаться слева от мнимой оси комплексной плоскости s=j.

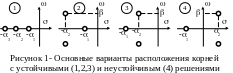
Характер устойчивого решения y(t) зависит от взаимного расположения корней характеристического уравнения. Для рассматриваемого уравнения с тремя корнями возможны следующие основные варианты их взаимного расположения, рис.1:

1  все корни вещественные: -₁; -₂; -₃;

2  два корня комплексно-сопряженные и один вещественный: -₁; -₂; причем ₁<₂;

3  два корня комплексно-сопряженные и один вещественный: -₁; -₂; причем ₁>₂;

4 – комплексные корни имеют положительную вещественную часть: -₁; ₂ (неустойчивое решение).

Д ля выделения в плоскости ВоА указанных подобластей 1,2,3 и 4 необходимо найти расположения корней, соответствующие границам 1-2, 1-3, 2-3 между этими подобластями, а также общую границу 3-4 устойчивого решения, рис.2.

Взаимосвязь корней с коэффициентами А и В определим по формулам Виета:

А = -(s₁+s₂+s₃);

B = (s₁s₂+s₁s₃+s₂s₃);

1 = -s₁s₂s₃.

Подставляя вместо s₁,s₂,s₃ выражения для корней, соответствующие искомым границам получим уравнения для этих границ в плоскости ВоА в параметрическом виде.

Для границы 1-2:

корни s₁ = -₁; s₂ = s₃ = -; _1;

коэффициенты A=₁+2;

B=2₁+²;

1=₁², где [).

Построить эту границу можно, изменяя  от 1 до . При этом будет обеспечено условие ₁(см.рис.2).

Для границы 1-3:

корни s₁ = s₂ = -; s₃ = -₃; ₃;

коэффициенты A=₃+2;

B=2₃+²;

1=₃², где (01].

Выполнение условия ₃ будет обеспечено при изменении  в интервале от 0 до 1.

Для границы 2-3:

корни s₁ = -; s_2,3 = -j;

коэффициенты A=-((- )+(-+j)+(--j))=3;

B=(-)(-+j)+(-)(--j)+(-+j)(--j)=

=3²+²;

1=-(- )(-+j)(--j)=(²+²), где (01].

Для границы 3-4:

корни s₁ = -₁; s_2,3 = j;

коэффициенты A=-((-₁ )+(j)+(-j))=₁;

B=(-₁)(j)+(-₁)(-j)+(j)(-j)=²;

1=-(-₁ )(j)(-j)=₁², где (0).

Примечание.

Выражения для искомых границ в данной задаче могут быть получены в явном виде В(А), однако параметрический вид решения обладает большей общностью и может быть распространен для задач анализа уравнений с более высоким порядком.

П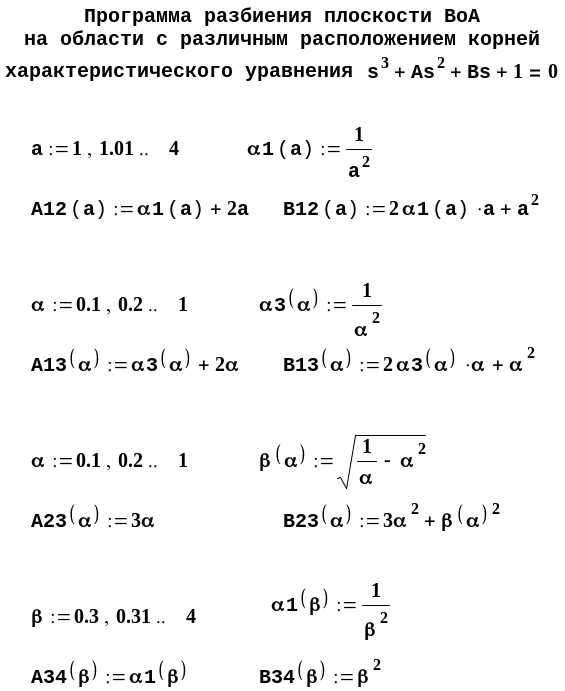 рограмма вычисления А и В для каждой из указанных границ в пакете Mathcad представлена ниже.

В программе величинами А12,В12, А13,В13, А23,В23, А34,В34 обозначены коэффициенты А и В, образующие соответственно границы 1-2, 1-3, 2-3 и 3-4. Остальные обозначения в программе совпадают с аналитическими выражениями в тексте и к разночтениям не приводят.

Следует отметить, что представленный алгоритм может быть реализован на любом формальном языке; математический пакет Mathcad в данном случае выбран из-за его удобного графического интерфейса.