
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Факультет автоматики и электромеханики
Кафедра высшей математики и физико-математического моделирования
Курсовая работа по курсу «Высшая математика» на тему:
«Моделирование и гармонический анализ аналого-цифрового преобразователя».
Выполнил: студент группы АТ-101
Ломакин В.А.
Проверил: Купцов В.С.
Воронеж 2011
Содержание
Тригонометрический ряд Фурье 4
Обобщения 6
Ряды Фурье в гильбертовом пространстве 6
Двойственность Понтрягина 7
Сходимость ряда Фурье 7
Введение
Спектральная (частотная) форма представления сигналов использует разложение сигнальных функций на периодические составляющие.
Периодичность гармонических колебаний исследовал еще в VI веке до нашей эры Пифагор и даже распространил его на описание гармонического движения небесных тел. Термин "spectrum" ("спектр") впервые применил И. Ньютон в 1571 году при описании разложения солнечного света, пропущенного через стеклянную призму, на многоцветную полосу. Он же дал и первую математическую трактовку периодичности волновых движений. В 18-м веке решениями волновых уравнений (в приложении к струнам) занимались Даниил Бернулли и Леонард Эйлер. По существу, уже Бернулли и Эйлер показали, что произвольные периодические функции представляют собой суммы простейших гармонических функций – синусов и косинусов кратных частот. Эти суммы получили название рядов Фурье, после того как в 1807 году французский инженер Жан Батист Фурье обосновал метод вычисления коэффициентов тригонометрического ряда, которым можно отображать с абсолютной точностью (при бесконечном числе членов ряда) или аппроксимировать с заданной точностью (при ограничении числа членов ряда) любую периодическую функцию, определенную на интервале одного периода T = b-a, и удовлетворяющую условиям Дирехле (ограниченная, кусочно-непрерывная, с конечным числом разрывов 1-го рода). Ряды Фурье в вещественной форме имеют следующий вид:
y(x) =(a0/2) +![]() (ak
cos(2kf1x) + bk
sin(2kf1x)), f1
= 1/T.
(ak
cos(2kf1x) + bk
sin(2kf1x)), f1
= 1/T.
ak = (2/T)![]() y(x)
cos(2kf1x) dx, bk
= (2/T)
y(x)
sin(2kf1x) dx.
y(x)
cos(2kf1x) dx, bk
= (2/T)
y(x)
sin(2kf1x) dx.
Разложение сигнала на гармонические функции получило название прямого преобразования Фурье. Обратный процесс – синтез сигнала по синусоидам – называется обратным преобразованием Фурье (inverse Fourier transform).
Теоретическая часть
Ряд Фурье — представление произвольной функции f с периодом τ в виде ряда

Этот ряд может быть также переписан в виде
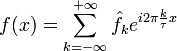 .
.
где
Ak — амплитуда k-го гармонического колебания,
![]() —
круговая частота гармонического
колебания,
—
круговая частота гармонического
колебания,
θk — начальная фаза k-го колебания,
![]() —
k-я комплексная амплитуда
—
k-я комплексная амплитуда
В более общем виде рядом Фурье элемента гильбертова пространства называется разложение этого элемента по ортогональному базису. Существует множество систем ортогональных функций: Уолша, Лагера, Котельникова…
Разложение функции в ряд Фурье является мощным инструментом при решении самых разных задач благодаря тому, что ряд Фурье прозрачным образом ведёт себя при дифференцировании, интегрировании, сдвиге функции по аргументу и свёртке функций.
